空间中直线与平面之间的位置关系
文档属性
| 名称 | 空间中直线与平面之间的位置关系 |  | |
| 格式 | rar | ||
| 文件大小 | 134.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-22 18:05:00 | ||
图片预览



文档简介
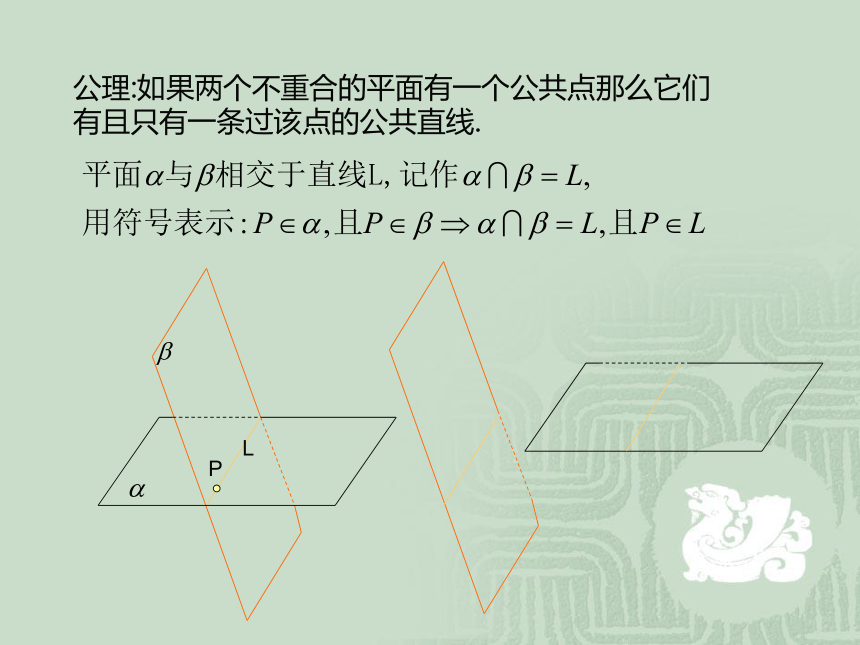
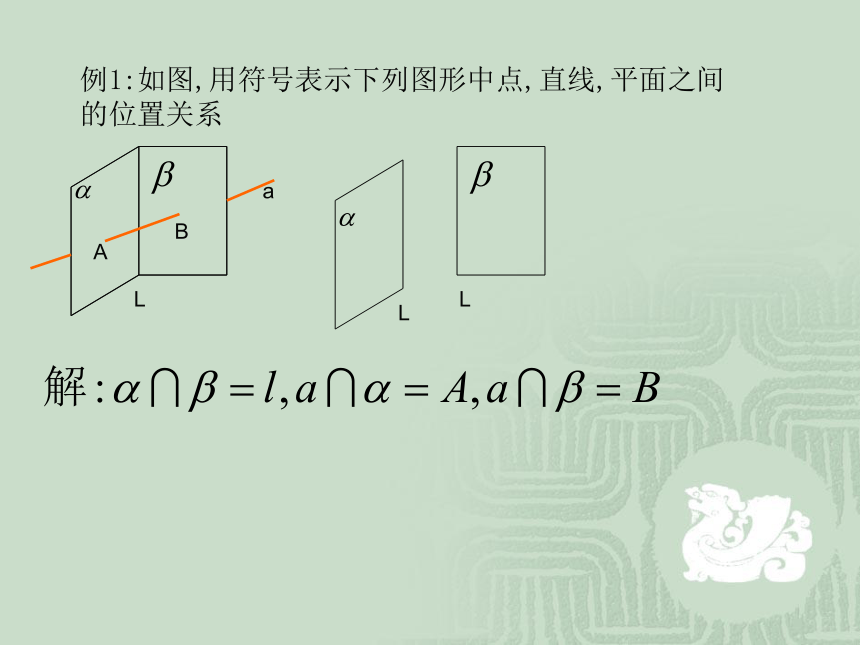
课件11张PPT。空间中直线与平面之间的位置关系主讲人:胡顺添公理:如果两个不重合的平面有一个公共点那么它们有且只有一条过该点的公共直线.PL例1:如图,用符号表示下列图形中点,直线,平面之间的位置关系LLa1,下列命题正确的是( )
(A)经过三点确定一个平面
(B)经过一条直线和一个点确定一个平面
(C)四边形确定一个平面
(D)两两相交且不共点的三条直线确定一个平面A[要不在同一直线的三个点]
B[点要在平面处]
C[不一定]
D[相当于三点确定一平面]
2,(1)不共面的四点可以确定几个平面
(2)共点的三条直线可以确定几个平面3,判断下列命题是否正确
(1)平面a与平面B相交,它们只有有限个公共点.
(2)经过一条直线和这条直线外的一点,有且只有一个平面
(3)经过两条相交直线,有且只有一个平面
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合.(1) 4个(2) 3个
空间中直线与直线之间的位置关系思考??同一平面两条直线有几种位置关系? 空间两条直线呢?无交点:平行直线
有一个交点:相交直线 思考:直线A’B与直线C’C的位置关系如何??我们把不在同一个平面内的两条直线叫做异面直线回忆:同一平面内,如果两条直线都与第三条直线平行,那么这两条直线平行
在空间中是否也有类似的规律?长方体ABCD-A’B’C’D’中,BB’//AA’,DD’//AA’
BB’与DD’平行吗?由长方体每条侧棱都平行知BB’//DD’公理4:平行于同一条直线的两条直线互相平行
这叫做空间平行线的传递性例2:如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,求证:
四边形ABCD是平行四边形证明:连接BD,
因为 EH是三角形ABD的中位线
所以 EH//BD,且EH=1/2BD.
同理,FG//BD,且FG=1/2BD,
因为 EH//FG,且EH=FG,
所以 四边形EFGH为平行四边形若AC=BD,那么四边形EFGH是什么图形?
连接AC,可知GH=1/2AC 在三角形ABD中EH=1/2BD
所以GH=EH, 所以四边形为菱形
C平面上如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补,
两条直线成四个角:究竟那个是所成的角?
异面直线所成的角:两条异面直线a与b经过空间任一点O作直线 a’//a,b’//b,我们把a’与b’所成的锐角或直角叫做异面直线a与b所成的角
(A)经过三点确定一个平面
(B)经过一条直线和一个点确定一个平面
(C)四边形确定一个平面
(D)两两相交且不共点的三条直线确定一个平面A[要不在同一直线的三个点]
B[点要在平面处]
C[不一定]
D[相当于三点确定一平面]
2,(1)不共面的四点可以确定几个平面
(2)共点的三条直线可以确定几个平面3,判断下列命题是否正确
(1)平面a与平面B相交,它们只有有限个公共点.
(2)经过一条直线和这条直线外的一点,有且只有一个平面
(3)经过两条相交直线,有且只有一个平面
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合.(1) 4个(2) 3个
空间中直线与直线之间的位置关系思考??同一平面两条直线有几种位置关系? 空间两条直线呢?无交点:平行直线
有一个交点:相交直线 思考:直线A’B与直线C’C的位置关系如何??我们把不在同一个平面内的两条直线叫做异面直线回忆:同一平面内,如果两条直线都与第三条直线平行,那么这两条直线平行
在空间中是否也有类似的规律?长方体ABCD-A’B’C’D’中,BB’//AA’,DD’//AA’
BB’与DD’平行吗?由长方体每条侧棱都平行知BB’//DD’公理4:平行于同一条直线的两条直线互相平行
这叫做空间平行线的传递性例2:如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,求证:
四边形ABCD是平行四边形证明:连接BD,
因为 EH是三角形ABD的中位线
所以 EH//BD,且EH=1/2BD.
同理,FG//BD,且FG=1/2BD,
因为 EH//FG,且EH=FG,
所以 四边形EFGH为平行四边形若AC=BD,那么四边形EFGH是什么图形?
连接AC,可知GH=1/2AC 在三角形ABD中EH=1/2BD
所以GH=EH, 所以四边形为菱形
C平面上如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补,
两条直线成四个角:究竟那个是所成的角?
异面直线所成的角:两条异面直线a与b经过空间任一点O作直线 a’//a,b’//b,我们把a’与b’所成的锐角或直角叫做异面直线a与b所成的角
