导数的应用--极值点
图片预览




文档简介
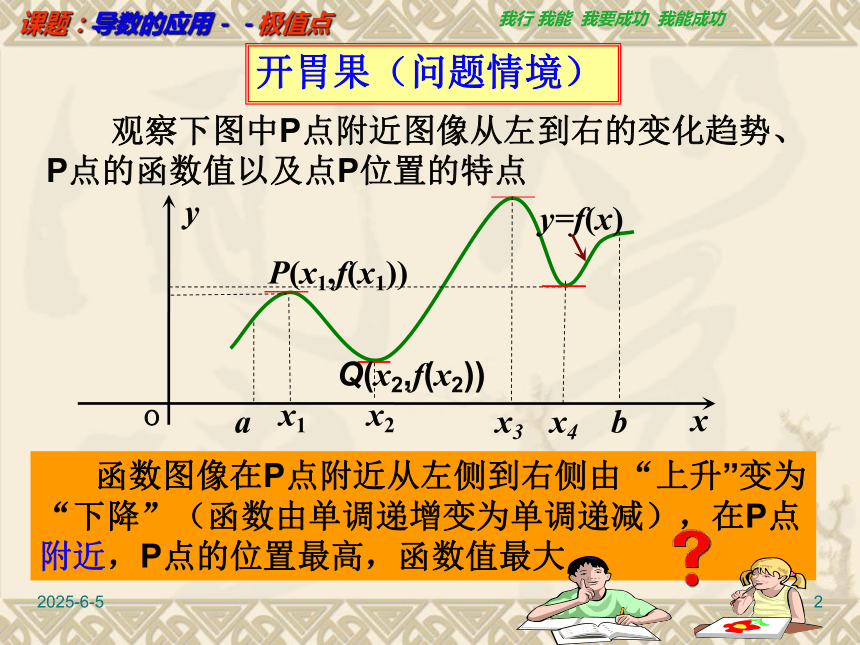
课件17张PPT。2019/3/151课题:导数的应用--极值点2019/3/152开胃果(问题情境) 观察下图中P点附近图像从左到右的变化趋势、P点的函数值以及点P位置的特点 函数图像在P点附近从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),在P点附近,P点的位置最高,函数值最大2019/3/153 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)﹤f (x0),我们就说f (x0)是函数f(x)的一个极大值,记作
y极大值= f (x0);如果对x0附近的所有的点,都有f(x)﹥f (x0),我们就说f (x0)是函数f(x)的一个极小值,记作y极小值=f (x0).
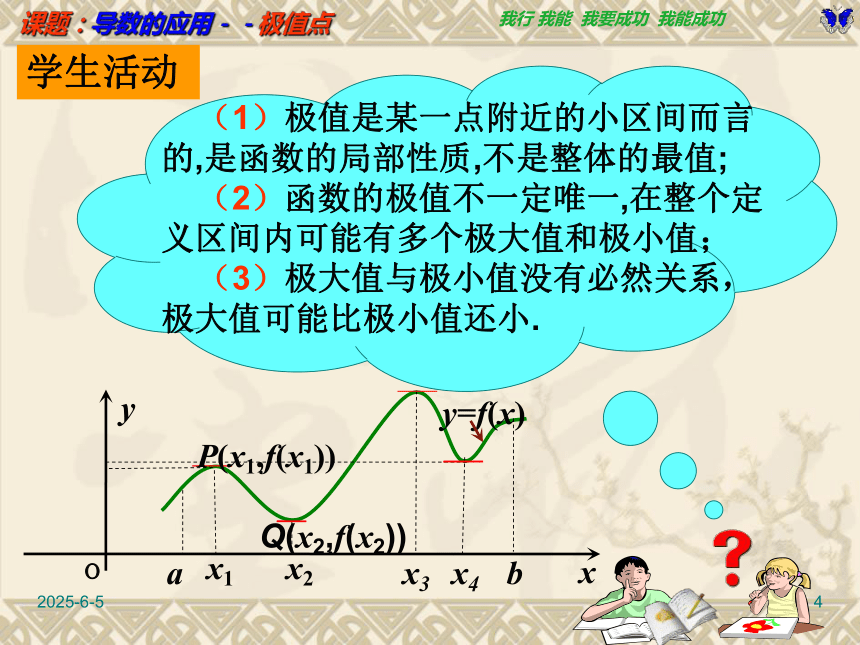
极大值与极小值同称为极值.函数极值的定义 数学建构2019/3/154 (1)极值是某一点附近的小区间而言 的,是函数的局部性质,不是整体的最值;
(2)函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
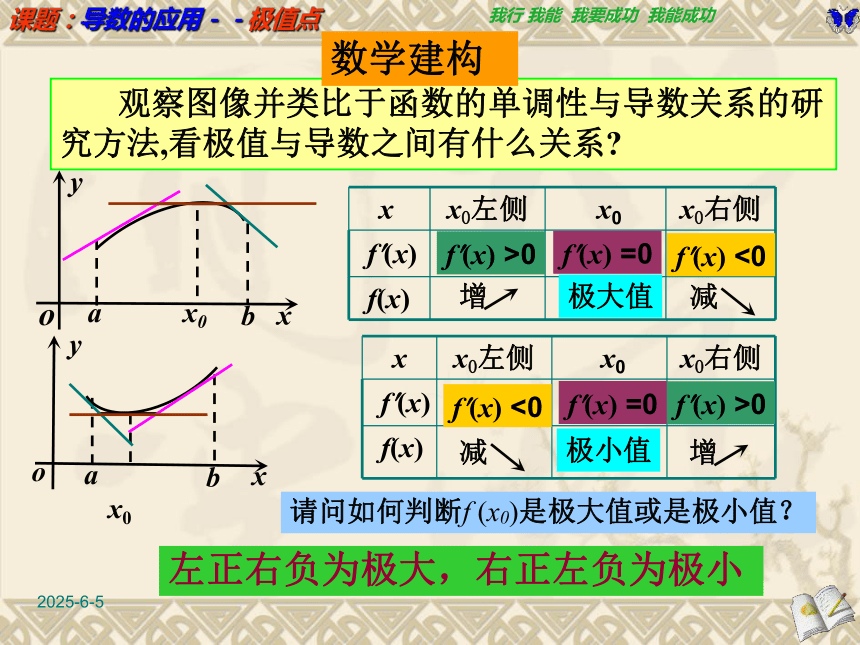
(3)极大值与极小值没有必然关系,极大值可能比极小值还小. 学生活动2019/3/155 观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?f?(x) >0f?(x) =0f?(x) <0极大值f?(x) <0f?(x) =0极小值f?(x) >0数学建构请问如何判断f (x0)是极大值或是极小值?左正右负为极大,右正左负为极小2019/3/156函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D学生活动2019/3/157小试牛刀篇(数学运用)2019/3/158小吃篇求下列函数的极值 2019/3/159渐入佳境篇探索: x =0是否为函数f(x)=x3的极值点? 若寻找可导函数极值点,可否只由f?(x)=0求得即可? f?(x)=3x2 当f?(x)=0时,x =0,而x =0不是该函数的极值点.f?(x0) =0 x0 是可导函数f(x)的极值点 x0左右侧导数异号 x0 是函数f(x)的极值点 f?(x0) =0注意:f /(x0)=0是函数取得极值的必要不充分条件2019/3/1510请思考求可导函数的极值的步骤:一览众山小 强调:要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.2019/3/1511 案例分析 函数 在 时有极值10,则a,b的值为( )(选自《高中数学中学教材全解》薛金星主编)
A、 或
B、 或
C、 D、 以上都不对 C,注意:f/(x0)=0是函数取得极值的必要不充分条件注意代入检验 2019/3/1512变式训练 函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 。注意:导数与方程、不等式的结合应用2019/3/1513庖丁解牛篇(感受高考)A注意:数形结合以及原函数与导函数图像的区别2019/3/1514.庖丁解牛篇(感受高考)略解:(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用2019/3/1515一吐为快篇(小结)本节课主要学习了哪些内容?请想一想?1、极值的判定方法
2、极值的求法注意点:1、f /(x0)=0是函数取得极值的必要不充分条件2、数形结合以及函数与方程思想的应用3、要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.2019/3/1516回味无穷篇(作业)1、课本P34习题1.3:3
2、创新训练3、思考题极值和最值的区别与联系2019/3/1517绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧 ,科学可改善物质生活,但数学能给予以上的一切。数学是人类最高超的成就,也是人类心灵最独特的创作。音乐能激发或抚慰情怀,行动指南:策略+方法+勤奋+信心+恒心=成功
y极大值= f (x0);如果对x0附近的所有的点,都有f(x)﹥f (x0),我们就说f (x0)是函数f(x)的一个极小值,记作y极小值=f (x0).
极大值与极小值同称为极值.函数极值的定义 数学建构2019/3/154 (1)极值是某一点附近的小区间而言 的,是函数的局部性质,不是整体的最值;
(2)函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
(3)极大值与极小值没有必然关系,极大值可能比极小值还小. 学生活动2019/3/155 观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?f?(x) >0f?(x) =0f?(x) <0极大值f?(x) <0f?(x) =0极小值f?(x) >0数学建构请问如何判断f (x0)是极大值或是极小值?左正右负为极大,右正左负为极小2019/3/156函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D学生活动2019/3/157小试牛刀篇(数学运用)2019/3/158小吃篇求下列函数的极值 2019/3/159渐入佳境篇探索: x =0是否为函数f(x)=x3的极值点? 若寻找可导函数极值点,可否只由f?(x)=0求得即可? f?(x)=3x2 当f?(x)=0时,x =0,而x =0不是该函数的极值点.f?(x0) =0 x0 是可导函数f(x)的极值点 x0左右侧导数异号 x0 是函数f(x)的极值点 f?(x0) =0注意:f /(x0)=0是函数取得极值的必要不充分条件2019/3/1510请思考求可导函数的极值的步骤:一览众山小 强调:要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.2019/3/1511 案例分析 函数 在 时有极值10,则a,b的值为( )(选自《高中数学中学教材全解》薛金星主编)
A、 或
B、 或
C、 D、 以上都不对 C,注意:f/(x0)=0是函数取得极值的必要不充分条件注意代入检验 2019/3/1512变式训练 函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 。注意:导数与方程、不等式的结合应用2019/3/1513庖丁解牛篇(感受高考)A注意:数形结合以及原函数与导函数图像的区别2019/3/1514.庖丁解牛篇(感受高考)略解:(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用2019/3/1515一吐为快篇(小结)本节课主要学习了哪些内容?请想一想?1、极值的判定方法
2、极值的求法注意点:1、f /(x0)=0是函数取得极值的必要不充分条件2、数形结合以及函数与方程思想的应用3、要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.2019/3/1516回味无穷篇(作业)1、课本P34习题1.3:3
2、创新训练3、思考题极值和最值的区别与联系2019/3/1517绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧 ,科学可改善物质生活,但数学能给予以上的一切。数学是人类最高超的成就,也是人类心灵最独特的创作。音乐能激发或抚慰情怀,行动指南:策略+方法+勤奋+信心+恒心=成功
