人教版数学八年级下册19.3课题学习选择方案同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册19.3课题学习选择方案同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 657.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 15:45:28 | ||
图片预览


文档简介
19.3 课题学习 选择方案 同步练习
一、单选题
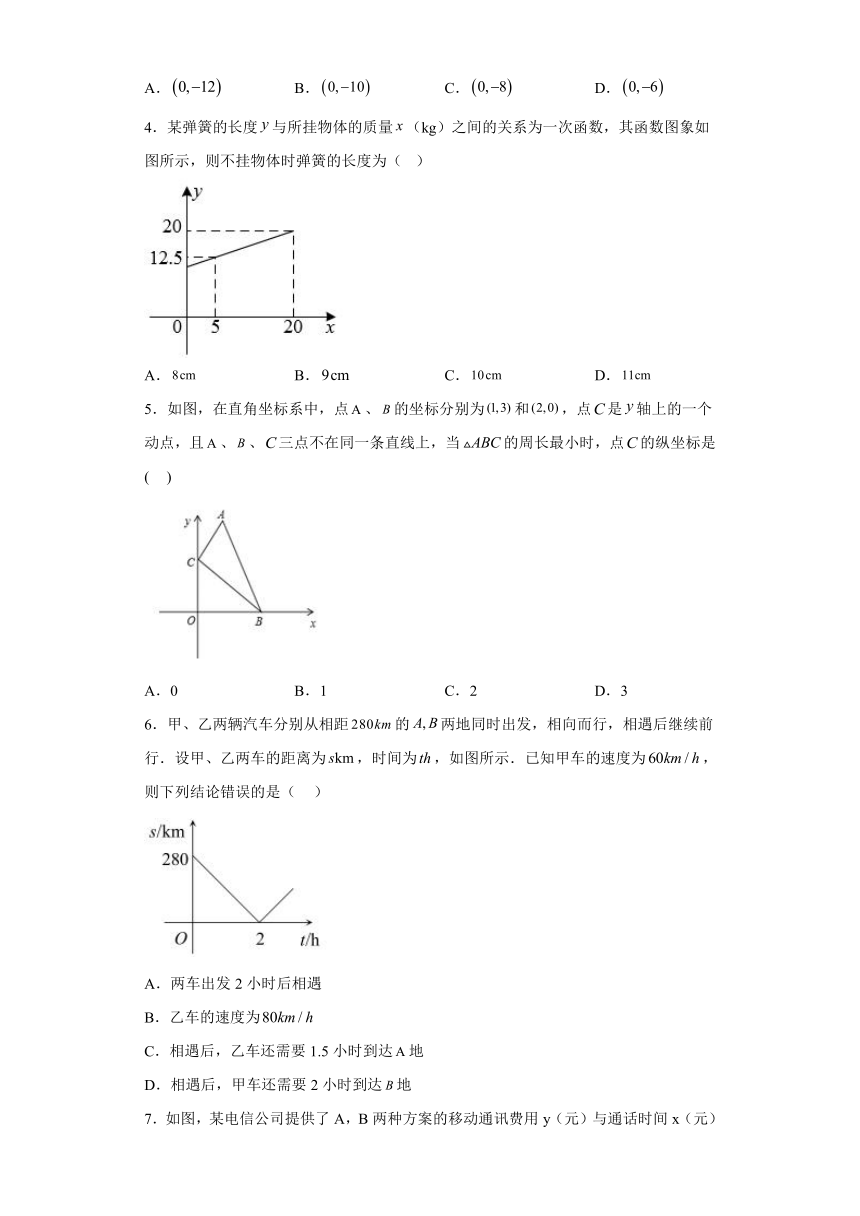
1.弹簧伸长的长度与所受拉力的大小成正比,某次实验中,小明记录了同一根弹簧的长度y(cm)和所挂重物的质量x(kg)(0≤x≤12)之间的部分对应数据如下表所示,下列说法中正确的是( )
x(kg) 0 0.5 1 1.5 2 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的正比例函数
B.当所挂重物的质量为5kg时,弹簧长度是14.5cm
C.物体质量由5kg增加到7kg,弹簧的长度增加了1cm
D.该弹簧不挂重物时的长度是10cm
2.如图,反映了某产品的销售收入与销售量之间的关系,反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.根据图中信息判断该公司在赢利时的销售量为( )
A.小于4件 B.大于4件 C.等于4件 D.不小于4件
3.如图,直线分别交轴、轴于、两点,在轴的负半轴上有一点,若将沿直线折叠得到,点在轴上,则点的坐标为( )
A. B. C. D.
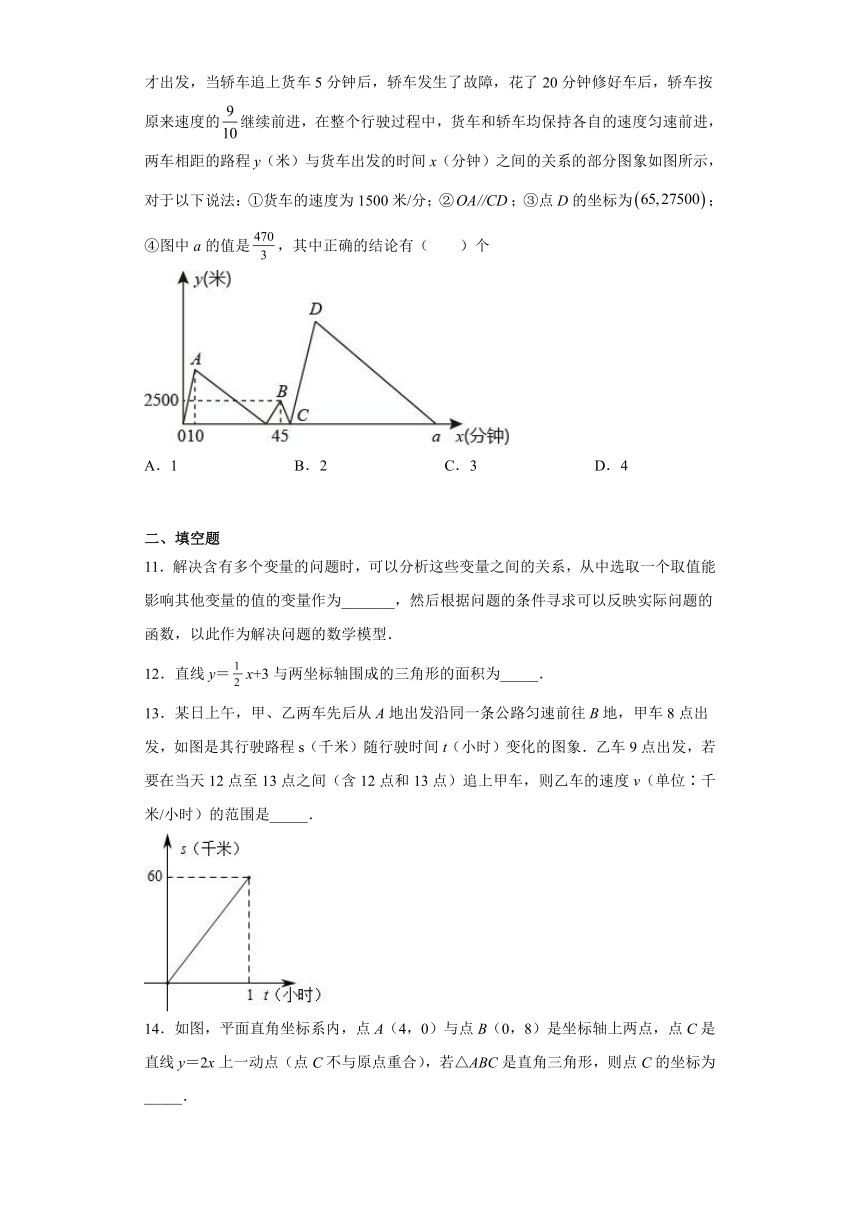
4.某弹簧的长度与所挂物体的质量(kg)之间的关系为一次函数,其函数图象如图所示,则不挂物体时弹簧的长度为( )
A. B. C. D.
5.如图,在直角坐标系中,点、的坐标分别为和,点是轴上的一个动点,且、、三点不在同一条直线上,当的周长最小时,点的纵坐标是( )
A.0 B.1 C.2 D.3
6.甲、乙两辆汽车分别从相距的两地同时出发,相向而行,相遇后继续前行.设甲、乙两车的距离为,时间为,如图所示.已知甲车的速度为,则下列结论错误的是( )
A.两车出发2小时后相遇
B.乙车的速度为
C.相遇后,乙车还需要1.5小时到达地
D.相遇后,甲车还需要2小时到达地
7.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个 B.2个 C.3个 D.4个
8.如图, 在平面直角坐标系中, 直线与坐标轴交于两点, 于点是线段上的一个动点, 连接, 将线段绕点逆时针旋转, 得到 线段, 连接, 则线段的最小值为( )
A. B.1 C. D.
9.如图,点的坐标为,点在直线上运动,当线段最短时,点的坐标为( )
A. B.
C. D.
10.货车和轿车分别沿同一路线从A地出发去B地,已知货车先出发10分钟后,轿车才出发,当轿车追上货车5分钟后,轿车发生了故障,花了20分钟修好车后,轿车按原来速度的继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;②;③点D的坐标为;④图中a的值是,其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
11.解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为_______,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
12.直线y=x+3与两坐标轴围成的三角形的面积为_____.
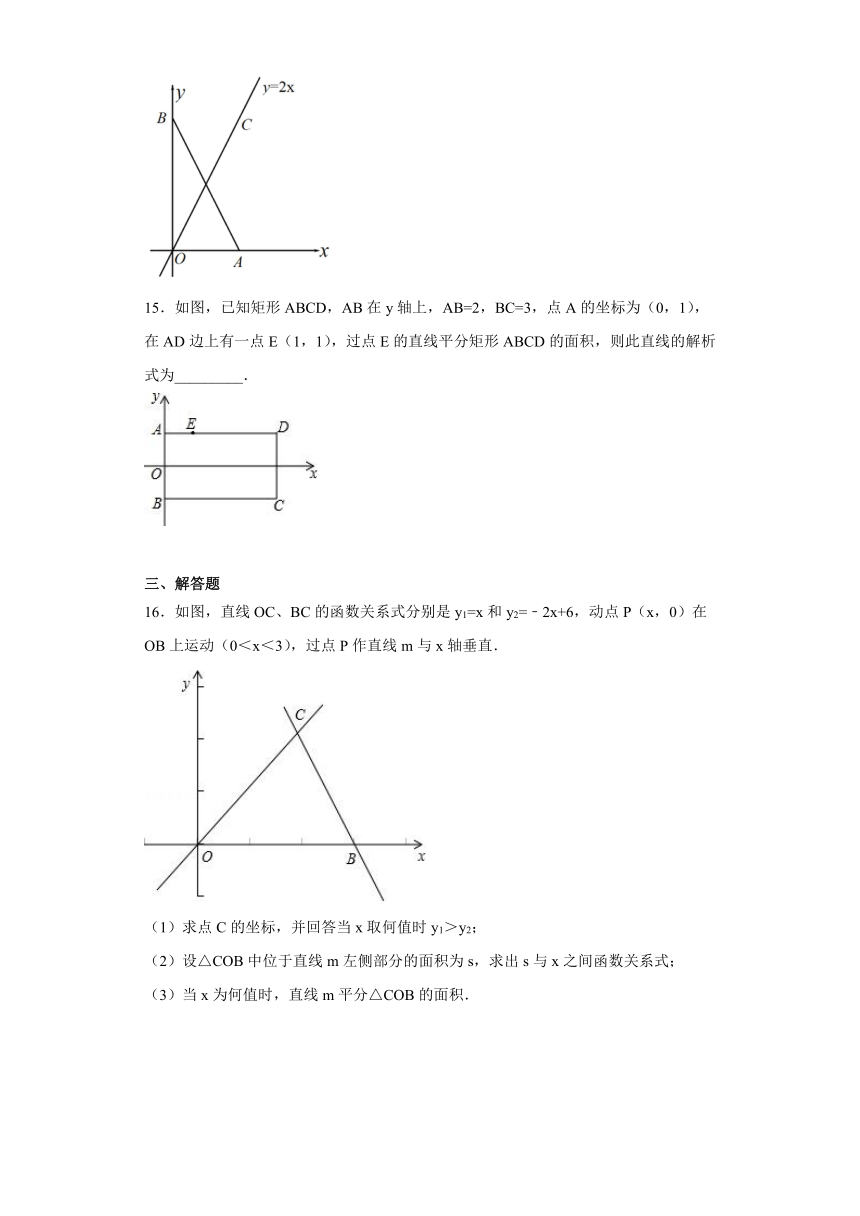
13.某日上午,甲、乙两车先后从A地出发沿同一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在当天12点至13点之间(含12点和13点)追上甲车,则乙车的速度v(单位∶千米/小时)的范围是_____.
14.如图,平面直角坐标系内,点A(4,0)与点B(0,8)是坐标轴上两点,点C是直线y=2x上一动点(点C不与原点重合),若△ABC是直角三角形,则点C的坐标为 _____.
15.如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(1,1),过点E的直线平分矩形ABCD的面积,则此直线的解析式为_________.
三、解答题
16.如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
(1)求点C的坐标,并回答当x取何值时y1>y2;
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式;
(3)当x为何值时,直线m平分△COB的面积.
17.节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水量与滴水时间的函数关系可以用显示水量的容器如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题:
(1)求与之间的函数关系式:
(2)计算在这种滴水状态下,一天(24小时)容器内的盛水量是多少升.
18.某文具店准备购甲、乙两种水笔进行销售,每支进价和利润如表:
甲水笔 乙水笔
每支进价(元) a
每支利润(元) 2 3
已知花费400元购进甲水笔的数量和花费800元购进乙水笔的数量相等.
(1)求甲,乙两种水笔每支进价分别为多少元.
(2)若该文具店准备拿出2000元全部用来购进这两种水笔,考虑顾客需求,要求购进甲种水笔的数量不超过乙种水笔数量的4倍,问该文具店如何进货能使利润最大,最大利润是多少元.
19.双休日小明同学和爸爸约定从家出发到滨海森林湿地公园游玩,路途中经过安徽名人馆,因爸爸已经参观过安徽名人馆,所以小明提前从家骑自行车出发到达安徽名人馆参观一会后按照相同的速度前往滨湖森林湿地公园.小明同学出发45分钟后爸爸骑摩托车以小明2倍的速度直接前往滨湖森林湿地公园,爸爸出发半小时后在途中遇到小明,爸爸没有停留直接前往公园.结果爸爸比小明早7.5分钟到达滨湖森林湿地公园.如图是小明和爸爸各自行走路与骑车时间的函数图象.
(1)小明的速度是: ,爸爸的速度是 ,点A的坐标 ;
(2)求小明家到滨湖森林湿地公园的路程.
(3)直接写出小明行走路程y(km)与行走时间x(h)的函数关系式.
20.某通讯公司推出了移动电话的两种计费方式,设一个月内使用移动电话主叫的时间为x分钟(x≥0),方式一,方式二的月使用费分别为y1元,y2元,两种计费方式被叫均免费.其中方式一月使用费详情见如表,方式二的月使用费y2元与主叫时间x分钟的函数图像如图所示.
月使用费/元 主叫限定时间/分钟 主叫超时费/(元/分钟) 被叫
方式一 38 120 0.1 免费
方式二
(1)根据题意填表:
表格一:
主叫时间x分钟 x=100 x=320 x>120
方式一计费/元 y1=
表格二
月使用费/元 主叫限定时间/分钟 主叫超时费/(元/分钟) 被叫
方式二 360 免费
(2)结合图像信息,求y2与x的函数解析式,并写出自变量的取值范围;
(3)选用哪种计费方式花钱少.
参考答案
1.D
2.B.
3.A
4.C
5.C
6.D
7.C
8.A
9.D
10.D
11.自变量
12.9.
13.
14.(4,8)或(,)或(,)
15.y=-2x+3.
16.(1)解方程组得
∴C点坐标为(2,2);
当x>2时,y1>y2
(2)作CD⊥x轴于点D,则D(2,0).
①s=x2(0②s=-x2+6x-6(2(3)直线m平分△AOB的面积,
则点P只能在线段OD,即0又△COB的面积等于3,
故x2=3×,解之得x=
17.(1)设w与t之间的函数关系式为,将代入,得:,
解得:,
故w与t之间的函数关系式为;
(2)由解析式可知,每小时滴水量为,当时,一天的滴水量,
即在这种滴水状态下一天的滴水量是升.
18.(1)解:由题意可得:,
解得,
经检验,是原分式方程的解,
,
答:甲,乙两种水笔每支进价分别为5元、10元.
(2)解:设利润为w元,甲种水笔购进x支,
,
,
∴y随x的增大而增大,
购进甲种水笔的数量不超过乙种水笔数量的4倍,
,
解得,,
∵x为整数,
∴当时,w取得最大值,最大值为733,
此时,,
答:该文具店购进甲种水笔266支,乙种水笔67支时,能使利润最大,最大利润是733元.
19.解:(1)小明的速度,
爸爸的速度,
,则,
故答案是:,,;
(2)设从爸爸追上小明的地点到公园路程为n(km),
,解得,
∴小明家到滨湖森林湿地公园的路程;
(3)设直线AB的解析式为:
,解得,
∴直线AB的解析式为:,
∴小明行走路程y(km)与行走时间x(h)的函数关系式为:.
20(1)解:方式一,
根据题意:当x≤120时,y1=38;
当x>120时,y1=38+0.1(x-120)=0.1x+26;
∴x=100时,y1=38;
x=320时,y1=0.1×320+26=58;
∴填表如下:
主叫时间x分钟 x=100 x=320 x>120
方式一计费/元 38 58 y1=0.1x+26
方式二,
填表如下:
月使用费/元 主叫限定时间/分钟 主叫超时费/(元/分钟) 被叫
方式二 58 360 0.1 免费
故答案为38,,58,0.1x+26,58,0.1.
(2)
解:根据题意:当0≤x≤360时,y2=58;
当x>360时,设y2=kx+b,
把(360,58),(480,70)代入得:,解得:,
∴当x>360时,y2=0.1x+22,
;
(3)
解:依题意画出两个函数的图像如下:
观察图像得:当x=320时,两种方式费用相同,都是58元;
当0≤x<320时,方式一花钱少;
当x>320时,方式二花钱少.
一、单选题
1.弹簧伸长的长度与所受拉力的大小成正比,某次实验中,小明记录了同一根弹簧的长度y(cm)和所挂重物的质量x(kg)(0≤x≤12)之间的部分对应数据如下表所示,下列说法中正确的是( )
x(kg) 0 0.5 1 1.5 2 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的正比例函数
B.当所挂重物的质量为5kg时,弹簧长度是14.5cm
C.物体质量由5kg增加到7kg,弹簧的长度增加了1cm
D.该弹簧不挂重物时的长度是10cm
2.如图,反映了某产品的销售收入与销售量之间的关系,反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.根据图中信息判断该公司在赢利时的销售量为( )
A.小于4件 B.大于4件 C.等于4件 D.不小于4件
3.如图,直线分别交轴、轴于、两点,在轴的负半轴上有一点,若将沿直线折叠得到,点在轴上,则点的坐标为( )
A. B. C. D.
4.某弹簧的长度与所挂物体的质量(kg)之间的关系为一次函数,其函数图象如图所示,则不挂物体时弹簧的长度为( )
A. B. C. D.
5.如图,在直角坐标系中,点、的坐标分别为和,点是轴上的一个动点,且、、三点不在同一条直线上,当的周长最小时,点的纵坐标是( )
A.0 B.1 C.2 D.3
6.甲、乙两辆汽车分别从相距的两地同时出发,相向而行,相遇后继续前行.设甲、乙两车的距离为,时间为,如图所示.已知甲车的速度为,则下列结论错误的是( )
A.两车出发2小时后相遇
B.乙车的速度为
C.相遇后,乙车还需要1.5小时到达地
D.相遇后,甲车还需要2小时到达地
7.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个 B.2个 C.3个 D.4个
8.如图, 在平面直角坐标系中, 直线与坐标轴交于两点, 于点是线段上的一个动点, 连接, 将线段绕点逆时针旋转, 得到 线段, 连接, 则线段的最小值为( )
A. B.1 C. D.
9.如图,点的坐标为,点在直线上运动,当线段最短时,点的坐标为( )
A. B.
C. D.
10.货车和轿车分别沿同一路线从A地出发去B地,已知货车先出发10分钟后,轿车才出发,当轿车追上货车5分钟后,轿车发生了故障,花了20分钟修好车后,轿车按原来速度的继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;②;③点D的坐标为;④图中a的值是,其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
11.解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为_______,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
12.直线y=x+3与两坐标轴围成的三角形的面积为_____.
13.某日上午,甲、乙两车先后从A地出发沿同一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在当天12点至13点之间(含12点和13点)追上甲车,则乙车的速度v(单位∶千米/小时)的范围是_____.
14.如图,平面直角坐标系内,点A(4,0)与点B(0,8)是坐标轴上两点,点C是直线y=2x上一动点(点C不与原点重合),若△ABC是直角三角形,则点C的坐标为 _____.
15.如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(1,1),过点E的直线平分矩形ABCD的面积,则此直线的解析式为_________.
三、解答题
16.如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
(1)求点C的坐标,并回答当x取何值时y1>y2;
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式;
(3)当x为何值时,直线m平分△COB的面积.
17.节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水量与滴水时间的函数关系可以用显示水量的容器如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题:
(1)求与之间的函数关系式:
(2)计算在这种滴水状态下,一天(24小时)容器内的盛水量是多少升.
18.某文具店准备购甲、乙两种水笔进行销售,每支进价和利润如表:
甲水笔 乙水笔
每支进价(元) a
每支利润(元) 2 3
已知花费400元购进甲水笔的数量和花费800元购进乙水笔的数量相等.
(1)求甲,乙两种水笔每支进价分别为多少元.
(2)若该文具店准备拿出2000元全部用来购进这两种水笔,考虑顾客需求,要求购进甲种水笔的数量不超过乙种水笔数量的4倍,问该文具店如何进货能使利润最大,最大利润是多少元.
19.双休日小明同学和爸爸约定从家出发到滨海森林湿地公园游玩,路途中经过安徽名人馆,因爸爸已经参观过安徽名人馆,所以小明提前从家骑自行车出发到达安徽名人馆参观一会后按照相同的速度前往滨湖森林湿地公园.小明同学出发45分钟后爸爸骑摩托车以小明2倍的速度直接前往滨湖森林湿地公园,爸爸出发半小时后在途中遇到小明,爸爸没有停留直接前往公园.结果爸爸比小明早7.5分钟到达滨湖森林湿地公园.如图是小明和爸爸各自行走路与骑车时间的函数图象.
(1)小明的速度是: ,爸爸的速度是 ,点A的坐标 ;
(2)求小明家到滨湖森林湿地公园的路程.
(3)直接写出小明行走路程y(km)与行走时间x(h)的函数关系式.
20.某通讯公司推出了移动电话的两种计费方式,设一个月内使用移动电话主叫的时间为x分钟(x≥0),方式一,方式二的月使用费分别为y1元,y2元,两种计费方式被叫均免费.其中方式一月使用费详情见如表,方式二的月使用费y2元与主叫时间x分钟的函数图像如图所示.
月使用费/元 主叫限定时间/分钟 主叫超时费/(元/分钟) 被叫
方式一 38 120 0.1 免费
方式二
(1)根据题意填表:
表格一:
主叫时间x分钟 x=100 x=320 x>120
方式一计费/元 y1=
表格二
月使用费/元 主叫限定时间/分钟 主叫超时费/(元/分钟) 被叫
方式二 360 免费
(2)结合图像信息,求y2与x的函数解析式,并写出自变量的取值范围;
(3)选用哪种计费方式花钱少.
参考答案
1.D
2.B.
3.A
4.C
5.C
6.D
7.C
8.A
9.D
10.D
11.自变量
12.9.
13.
14.(4,8)或(,)或(,)
15.y=-2x+3.
16.(1)解方程组得
∴C点坐标为(2,2);
当x>2时,y1>y2
(2)作CD⊥x轴于点D,则D(2,0).
①s=x2(0
则点P只能在线段OD,即0
故x2=3×,解之得x=
17.(1)设w与t之间的函数关系式为,将代入,得:,
解得:,
故w与t之间的函数关系式为;
(2)由解析式可知,每小时滴水量为,当时,一天的滴水量,
即在这种滴水状态下一天的滴水量是升.
18.(1)解:由题意可得:,
解得,
经检验,是原分式方程的解,
,
答:甲,乙两种水笔每支进价分别为5元、10元.
(2)解:设利润为w元,甲种水笔购进x支,
,
,
∴y随x的增大而增大,
购进甲种水笔的数量不超过乙种水笔数量的4倍,
,
解得,,
∵x为整数,
∴当时,w取得最大值,最大值为733,
此时,,
答:该文具店购进甲种水笔266支,乙种水笔67支时,能使利润最大,最大利润是733元.
19.解:(1)小明的速度,
爸爸的速度,
,则,
故答案是:,,;
(2)设从爸爸追上小明的地点到公园路程为n(km),
,解得,
∴小明家到滨湖森林湿地公园的路程;
(3)设直线AB的解析式为:
,解得,
∴直线AB的解析式为:,
∴小明行走路程y(km)与行走时间x(h)的函数关系式为:.
20(1)解:方式一,
根据题意:当x≤120时,y1=38;
当x>120时,y1=38+0.1(x-120)=0.1x+26;
∴x=100时,y1=38;
x=320时,y1=0.1×320+26=58;
∴填表如下:
主叫时间x分钟 x=100 x=320 x>120
方式一计费/元 38 58 y1=0.1x+26
方式二,
填表如下:
月使用费/元 主叫限定时间/分钟 主叫超时费/(元/分钟) 被叫
方式二 58 360 0.1 免费
故答案为38,,58,0.1x+26,58,0.1.
(2)
解:根据题意:当0≤x≤360时,y2=58;
当x>360时,设y2=kx+b,
把(360,58),(480,70)代入得:,解得:,
∴当x>360时,y2=0.1x+22,
;
(3)
解:依题意画出两个函数的图像如下:
观察图像得:当x=320时,两种方式费用相同,都是58元;
当0≤x<320时,方式一花钱少;
当x>320时,方式二花钱少.
