人教A版(2019)2022-2023学年高一下学期素质测试数学试题(三)(含解析)
文档属性
| 名称 | 人教A版(2019)2022-2023学年高一下学期素质测试数学试题(三)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 00:00:00 | ||
图片预览




文档简介
人教A版(2019)2022-2023学年高一下学期素质测试
数学试题(三)
一、单选题
1.在复平面内,复数对应点的坐标是,是复数的共轭复数,则( )
A. B. C. D.
2.已知点在线段上,且,则等于( )
A. B. C. D.
3.设m,n是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.设,,,则( )
A. B. C. D.
5.下列命题正确的是( )
A.如果一个平面内有无数条直线与另一个平面平行,则这两个平面平行
B.如果两个平面垂直于同一个平面,那么这两个平面平行
C.如果一条直线与平面内的一条直线平行,则该直线与此平面平行
D.如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直
6.如图在RtABC中,AB=BC=6,动点D,E,F分别在边BC,AC,AB上,四边形BDEF为矩形,剪去矩形BDEF后,将剩余部分绕AF所在直线旋转一周,得到一个几何体,则当该几何体的表面积最大时,BD=( )
A.2 B.3 C.4 D.3
7.设是的重心,且,若外接圆的半径为1,则的面积为( )
A. B. C. D.
8.底面半径为2,高为5的圆柱内挖去一个半径为2的球体,剩余的几何体的体积是( )
A. B.9π C. D.20π
二、多选题
9.下列命题正确的是( )
A.若为复数,则
B.若为向量,则
C.若为复数,且,则
D.若为向量,且,则
10.在△ABC中,角A,B,C的对边分别为a,b,c,若,B=30°,则使此三角形只有唯一解的b的值可以是( )
A. B.3 C.5 D.
11.如图,正方体的中心为分别为的中点,分别为线段上的动点(包含端点),则( )
A.对于任意点平面
B.存在点,使得平面平面
C.三棱锥的体积为定值
D.存在点,使得平面
12.下列命题中,正确的是( )
A.在中,,
B.在锐角中,不等式恒成立
C.在中,若,则必是等腰直角三角形
D.在中,若,,则必是等边三角形
三、填空题
13.已知向量,当与的夹角为锐角时,则实数m的取值范围是______.
14.在梯形中,,则的值是___________.
15.已知等腰直角三角形的直角边长为,且其顶点都在球上,若球的体积为,则三棱锥的体积为______.
16.在三角形中,已知,,若,则的值为__________.
四、解答题
17.已知z是复数,和均为实数,其中i是虚数单位.
(1)求复数z的共轭复数;
(2)记,若复数对应的点在第三象限,求实数m的取值范围.
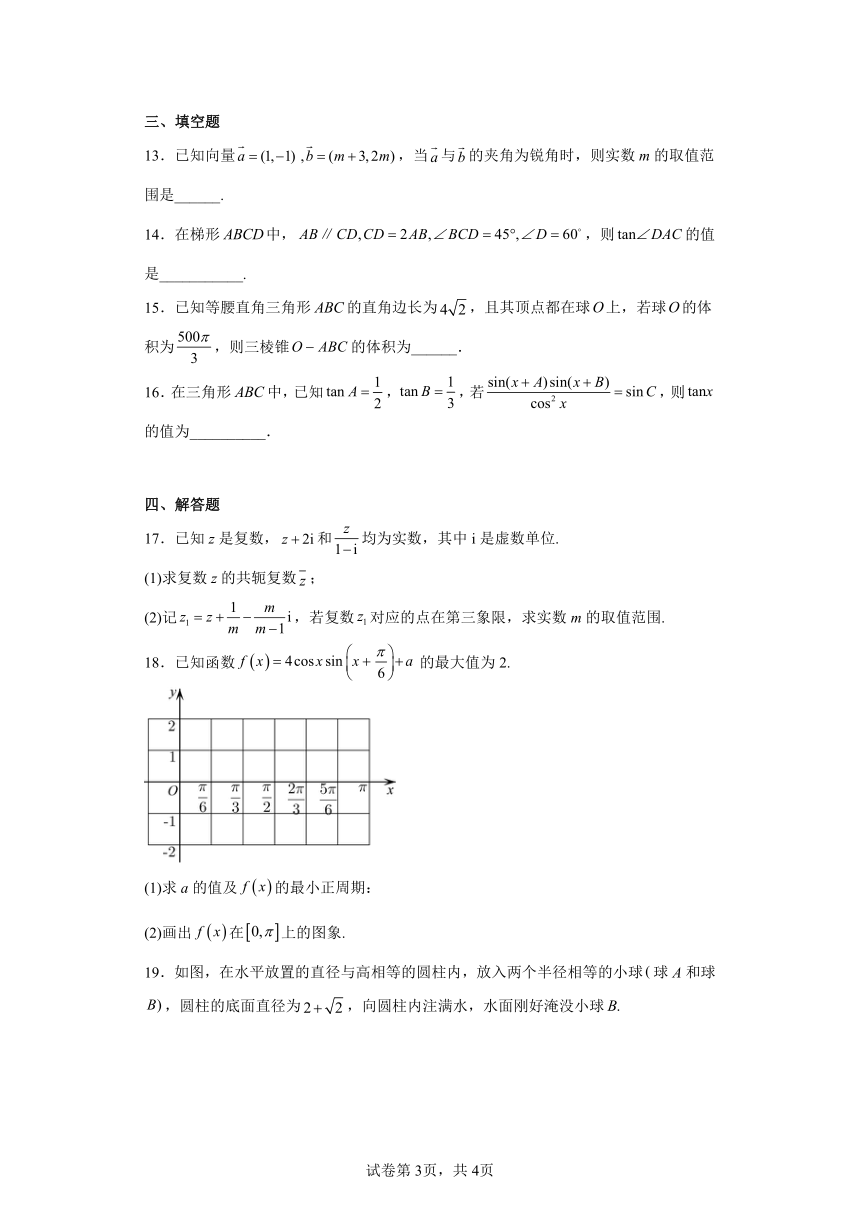
18.已知函数的最大值为2.
(1)求a的值及的最小正周期:
(2)画出在上的图象.
19.如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球球A和球,圆柱的底面直径为,向圆柱内注满水,水面刚好淹没小球
(1)求球A的体积;
(2)求圆柱的侧面积与球B的表面积之比.
20.已知函数,且满足________.从①函数的图象关于点对称;②函数的最大值为2;③函数的图象经过点.这三个条件中任选一个补充到上面的横线上,并解答下面的问题:
(1)求实数a的值并求函数的单调递增区间;
(2)已知函数,若对任意的,总存在,使得,求实数m的取值范围.
21.P为正方形ABCD所在平面外一点,E,F,G分别为PD,AB,DC的中点,如图.求证:
(1)AE∥平面PCF;
(2)平面PCF∥平面AEG.
22.在△ABC中,a,b,c分别为内角A,B,C的对边,△ABC的面积.
(1)若,求的值;
(2)求的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据点的坐标,写出,再写出,利用复数除法法则计算即可.
【详解】因为复数对应点的坐标是,
所以,则
所以.
故选:A.
2.C
【分析】利用平面向量加法法则可得出关于的表达式.
【详解】,解得.
故选:C.
3.C
【分析】举出的反例可判断A;举出异面的反例可判断B;根据两条平行线其中一条垂直平面,那么另外一条也垂直平面可判断C;举出平行的反例可判断D.
【详解】对于A,如图,
此时,A错误;
对于B,如图,
此时异面,B错误;
对于C,由性质定理: “如果在两条平行线中,有一条垂直于平面,那么另一条也垂直于这个平面.”可知,C正确;
对于D,
此时,D错误.
故选:C.
4.C
【分析】先由倍角公式得,再由正弦差角公式得及诱导公式得,由正弦函数单调性比较大小即可.
【详解】,,
,由正弦函数的单调性知,.
故选:C.
5.D
【分析】根据空间中线线、线面、面面的位置关系判断即可.
【详解】解:对于A:如果一个平面内有无数条直线与另一个平面平行,则这两个平面平行或相交,故A错误;
对于B:如果两个平面垂直于同一个平面,那么这两个平面平行或相交,故B错误;
对于C:如果一条直线与平面内的一条直线平行,则该直线与此平面平行或该直线在此平面内,故C错误;
对于D:如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直,此为面面垂直的性质定理,故D正确;
故选:D
6.B
【分析】根据已知条件,表面积是圆锥表面积加圆柱侧面积,再应用基本不等式求最值及取等条件即可.
【详解】设BD=x,BF=y,其中x、y(0,6);由题意知,,所以x+y=6;
所以所求几何体的表面积为:
当且仅当x=y=3,即BD=3时取得“=”;
即所得几何体的表面积最大时,BD=3.
故选:B.
7.B
【分析】根据是三角形的重心得到,结合已知条件进行化简,求得,由此判断出三角形是等边三角形,再结合三角形外接圆半径以及正弦定理,求得三角形的边长,由此求得三角形的面积.
【详解】∵是的重心,∴,
则,代入得,,
∵不共线,∴且,
即,∴是等边三角形,又外接圆的半径为1,
∴由正弦定理得,,则,
∴.
故选:B.
【点睛】本小题主要考查三角形重心的向量表示,考查正弦定理的运用,考查化归与转化的数学思想方法,属于中档题.
8.A
【解析】由圆柱的体积公式,求得圆柱的体积为,由球的体积公式,求得球的体积,
进而求得剩余的几何体的体积,得到答案.
【详解】由圆柱的体积公式,可得圆柱的体积为,
其中半径为2的球的体积为,
所以剩余的几何体的体积为.
故选:A.
【点睛】本题主要考查了组合体的体积的计算,其中解答中熟记圆柱和球的体积公式,准确运算是解答的关键,着重考查运算与求解能力.
9.AD
【分析】根据复数运算、向量运算的知识对选项进行分析,从而确定正确选项.
【详解】令,,,
,
,,
,A对;
,不一定成立,B错;
,,
,,
,C错.
将两边平方并化简得,D对.
故选:AD
10.BD
【分析】由题意,则角A只有一个解,有或且,转化为边的关系即可.
【详解】由正弦定理得,,要使此三角形只有唯一解,此三角形时有且只有唯一解,则A只有一个,
则或且,
所以或,选项BD符合.
故选:BD.
11.BC
【分析】选项A,当与重合时,可判断;
选项B,当为的中点时,可证明平面(平面),即可判断;
选项C,先证明平面,再由点到平面的距离为定值,而的面积是定值,可判断;
选项D,先证明平面平面,即可判断.
【详解】
选项A,连接,当与重合时,平面平面,此时直线与平面相交,A错误;
选项B,四边形为正方形,,当为的中点时,,
平面平面,
平面(平面),平面平面平面B正确;
选项C,在正方体中,
四边形为平行四边形,平面平面平面,点到平面的距离为定值,而的面积是定值,则三棱锥的体积为定值,正确;
选项D,平面,同理平面,且平面平面平面,又平面平面,D错误.
故选:BC.
12.ABD
【解析】对于选项在中,由正弦定理可得,即可判断出正误;对于选项在锐角中,由,可得,即可判断出正误;对于选项在中,由,利用正弦定理可得:,得到或即可判断出正误;对于选项在中,利用余弦定理可得:,代入已知可得,又,即可得到的形状,即可判断出正误.
【详解】对于,由,可得:,利用正弦定理可得:,正确;
对于,在锐角中,,,
,,
,因此不等式恒成立,正确;
对于,在中,由,利用正弦定理可得:,
,
,,
或,
或,
是等腰三角形或直角三角形,因此是假命题,错误.
对于,由于,,由余弦定理可得:,
可得,解得,可得,故正确.
故选:.
【点睛】本题考查正弦定理与余弦定理及三角形边角关系,主要涉及的考点是三角形内角的诱导公式的应用,同时考查正弦定理进行边角转化,属于中等题.
13.且
【分析】根据与的夹角为锐角,可得,且与不共线,然后建立关于的关系式,再求出的取值范围.
【详解】解:因为与的夹角为锐角,向量,
所以,且与不共线,
所以且,解得且,
所以的取值范围是且;
故答案为:且.
14.
【分析】设,根据正弦定理得出,,相除后化简即可得解.
【详解】设,则.
在中,,
在中,,
两式相除得,,
即,
因为,
所以可得,
所以.
故答案为:
15.16
【分析】根据球的体积为,求得球的半径,再由等腰直角三角形外接圆的圆心为线段的中点,求得,即为三棱锥的高,再由锥体的体积公式求解.
【详解】如图所示:
等腰直角三角形的直角边为,斜边,其外接圆的圆心为线段的中点,
所以是三棱锥的高,
设球的半径为,
因为,
所以,又,
所以,
所以三棱锥的体积为.
故答案为:16
16.或
【分析】由,解出A,B,C的正余弦值,将等式化简后代入,解出.
【详解】因为,,,,
所以,,,,
.
,
即,
所以,解得或.
故答案为:或.
17.(1)
(2)
【分析】(1)设,分别代入和,再根据两者均为实数可求得,,进而可求得复数z的共轭复数;
(2)化简,再根据复数对应的点在第三象限可建立不等式组,求解即可.
【详解】(1)设,则
由为实数,则,所以,
由为实数,则,所以
则,复数z的共轭复数.
(2)由(1)可知,
由对应的点在第三象限,得,即,
解得
故实数m的取值范围为
18.(1),最小正周期
(2)答案见解析
【解析】(1)
的最大值为2,
所以,最小正周期.
(2)
由(1)知,列表:
x 0
1 2 0 0 1
画图如下:
19.(1)
(2)
【分析】(1)根据圆柱的轴截面分析即可;
(2)直接利用球表面积、圆柱的侧面积公式计算即可.
【详解】(1)设圆柱的底面半径为R,小球的半径为r,且,
由圆柱与球的性质知,
即,
,
球A的体积为
(2)球B的表面积,
圆柱的侧面积,
圆柱的侧面积与球B的表面积之比为
20.(1),;
(2).
【分析】(1)由二倍角公式、两角差的正弦公式化函数为一个角的一个三角函数形式,
选①,由求得,再由正弦函数性质得单调增区间;选②,由结合正弦函数的最大值求得,再由正弦函数的单调性求得增区间;选③,由求得,再由正弦函数的单调性得增区间;
(2)求出的最大值,由可得参数范围.
【详解】(1)由条件知
若选①,则,解得,,
由,解得,,
所以函数的单调递增区间为.
若选②,则函数的最大值为,解得,,
由,解得,,
所以函数的单调递增区间为.
若选③,则,
所以,,
由,解得,,
所以函数的单调递增区间为.
(2)由题意可知只需即可.
当时,,所以,
因此函数的最大值为1.
令,则,则
当即时,函数的最大值为,于是,
整理得,解得,均满足,所以;
当即时,函数的最大值为,于是,无实解;
综上所述,实数m的取值范围为.
21.(1)证明见解析
(2)证明见解析
【分析】(1)取PC中点H,分别连接EH,FH,根据E,F,H分别为PD,AB,PC的中点,得到EAFH为平行四边形,从而EA∥FH,再利用线面平行的判定定理证明;
(2)根据E,G分别为PD,CD的中点,得到EG∥PC,利用线面平行的判定定理得到EG∥平面PCF,再利用面面平行的判定定理证明.
【详解】(1)证明:如图所示:
,
取PC中点H,分别连接EH,FH,
∵E,F,H分别为PD,AB,PC的中点,
∴,
∴EAFH为平行四边形.
∴EA∥FH.
又平面PCF,平面PCF,
∴AE∥平面PCF.
(2)∵E,G分别为PD,CD的中点,
∴EG∥PC.
又平面PCF,平面PCF,
∴EG∥平面PCF.
由(1)知AE∥平面PCF,EG∩AE=E.
∴平面PCF∥平面AEG.
22.(1)或
(2)
【分析】(1)由正弦定理化简可得,由可得,结合余弦定理得,换元求出其值,由正弦定理即可得答案;
(2)由得 ,结合余弦定理得,变形为,换元,可得,结合三角函数的性质可得不等式,即可求得答案.
【详解】(1)因为,由正弦定理得:,
即,即,
因为 ,所以,即,
由得:;
由得:,即,即,
由余弦定理可得:,
故,则,
令,则,解得 ,
由正弦定理得:,故的值为或;
(2)由得:,即,
由余弦定理可得:,
即,
故,
令,则,即,
由得,故,
故,即得 ,
故的取值范围是.
答案第1页,共2页
答案第1页,共2页
数学试题(三)
一、单选题
1.在复平面内,复数对应点的坐标是,是复数的共轭复数,则( )
A. B. C. D.
2.已知点在线段上,且,则等于( )
A. B. C. D.
3.设m,n是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.设,,,则( )
A. B. C. D.
5.下列命题正确的是( )
A.如果一个平面内有无数条直线与另一个平面平行,则这两个平面平行
B.如果两个平面垂直于同一个平面,那么这两个平面平行
C.如果一条直线与平面内的一条直线平行,则该直线与此平面平行
D.如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直
6.如图在RtABC中,AB=BC=6,动点D,E,F分别在边BC,AC,AB上,四边形BDEF为矩形,剪去矩形BDEF后,将剩余部分绕AF所在直线旋转一周,得到一个几何体,则当该几何体的表面积最大时,BD=( )
A.2 B.3 C.4 D.3
7.设是的重心,且,若外接圆的半径为1,则的面积为( )
A. B. C. D.
8.底面半径为2,高为5的圆柱内挖去一个半径为2的球体,剩余的几何体的体积是( )
A. B.9π C. D.20π
二、多选题
9.下列命题正确的是( )
A.若为复数,则
B.若为向量,则
C.若为复数,且,则
D.若为向量,且,则
10.在△ABC中,角A,B,C的对边分别为a,b,c,若,B=30°,则使此三角形只有唯一解的b的值可以是( )
A. B.3 C.5 D.
11.如图,正方体的中心为分别为的中点,分别为线段上的动点(包含端点),则( )
A.对于任意点平面
B.存在点,使得平面平面
C.三棱锥的体积为定值
D.存在点,使得平面
12.下列命题中,正确的是( )
A.在中,,
B.在锐角中,不等式恒成立
C.在中,若,则必是等腰直角三角形
D.在中,若,,则必是等边三角形
三、填空题
13.已知向量,当与的夹角为锐角时,则实数m的取值范围是______.
14.在梯形中,,则的值是___________.
15.已知等腰直角三角形的直角边长为,且其顶点都在球上,若球的体积为,则三棱锥的体积为______.
16.在三角形中,已知,,若,则的值为__________.
四、解答题
17.已知z是复数,和均为实数,其中i是虚数单位.
(1)求复数z的共轭复数;
(2)记,若复数对应的点在第三象限,求实数m的取值范围.
18.已知函数的最大值为2.
(1)求a的值及的最小正周期:
(2)画出在上的图象.
19.如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球球A和球,圆柱的底面直径为,向圆柱内注满水,水面刚好淹没小球
(1)求球A的体积;
(2)求圆柱的侧面积与球B的表面积之比.
20.已知函数,且满足________.从①函数的图象关于点对称;②函数的最大值为2;③函数的图象经过点.这三个条件中任选一个补充到上面的横线上,并解答下面的问题:
(1)求实数a的值并求函数的单调递增区间;
(2)已知函数,若对任意的,总存在,使得,求实数m的取值范围.
21.P为正方形ABCD所在平面外一点,E,F,G分别为PD,AB,DC的中点,如图.求证:
(1)AE∥平面PCF;
(2)平面PCF∥平面AEG.
22.在△ABC中,a,b,c分别为内角A,B,C的对边,△ABC的面积.
(1)若,求的值;
(2)求的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据点的坐标,写出,再写出,利用复数除法法则计算即可.
【详解】因为复数对应点的坐标是,
所以,则
所以.
故选:A.
2.C
【分析】利用平面向量加法法则可得出关于的表达式.
【详解】,解得.
故选:C.
3.C
【分析】举出的反例可判断A;举出异面的反例可判断B;根据两条平行线其中一条垂直平面,那么另外一条也垂直平面可判断C;举出平行的反例可判断D.
【详解】对于A,如图,
此时,A错误;
对于B,如图,
此时异面,B错误;
对于C,由性质定理: “如果在两条平行线中,有一条垂直于平面,那么另一条也垂直于这个平面.”可知,C正确;
对于D,
此时,D错误.
故选:C.
4.C
【分析】先由倍角公式得,再由正弦差角公式得及诱导公式得,由正弦函数单调性比较大小即可.
【详解】,,
,由正弦函数的单调性知,.
故选:C.
5.D
【分析】根据空间中线线、线面、面面的位置关系判断即可.
【详解】解:对于A:如果一个平面内有无数条直线与另一个平面平行,则这两个平面平行或相交,故A错误;
对于B:如果两个平面垂直于同一个平面,那么这两个平面平行或相交,故B错误;
对于C:如果一条直线与平面内的一条直线平行,则该直线与此平面平行或该直线在此平面内,故C错误;
对于D:如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直,此为面面垂直的性质定理,故D正确;
故选:D
6.B
【分析】根据已知条件,表面积是圆锥表面积加圆柱侧面积,再应用基本不等式求最值及取等条件即可.
【详解】设BD=x,BF=y,其中x、y(0,6);由题意知,,所以x+y=6;
所以所求几何体的表面积为:
当且仅当x=y=3,即BD=3时取得“=”;
即所得几何体的表面积最大时,BD=3.
故选:B.
7.B
【分析】根据是三角形的重心得到,结合已知条件进行化简,求得,由此判断出三角形是等边三角形,再结合三角形外接圆半径以及正弦定理,求得三角形的边长,由此求得三角形的面积.
【详解】∵是的重心,∴,
则,代入得,,
∵不共线,∴且,
即,∴是等边三角形,又外接圆的半径为1,
∴由正弦定理得,,则,
∴.
故选:B.
【点睛】本小题主要考查三角形重心的向量表示,考查正弦定理的运用,考查化归与转化的数学思想方法,属于中档题.
8.A
【解析】由圆柱的体积公式,求得圆柱的体积为,由球的体积公式,求得球的体积,
进而求得剩余的几何体的体积,得到答案.
【详解】由圆柱的体积公式,可得圆柱的体积为,
其中半径为2的球的体积为,
所以剩余的几何体的体积为.
故选:A.
【点睛】本题主要考查了组合体的体积的计算,其中解答中熟记圆柱和球的体积公式,准确运算是解答的关键,着重考查运算与求解能力.
9.AD
【分析】根据复数运算、向量运算的知识对选项进行分析,从而确定正确选项.
【详解】令,,,
,
,,
,A对;
,不一定成立,B错;
,,
,,
,C错.
将两边平方并化简得,D对.
故选:AD
10.BD
【分析】由题意,则角A只有一个解,有或且,转化为边的关系即可.
【详解】由正弦定理得,,要使此三角形只有唯一解,此三角形时有且只有唯一解,则A只有一个,
则或且,
所以或,选项BD符合.
故选:BD.
11.BC
【分析】选项A,当与重合时,可判断;
选项B,当为的中点时,可证明平面(平面),即可判断;
选项C,先证明平面,再由点到平面的距离为定值,而的面积是定值,可判断;
选项D,先证明平面平面,即可判断.
【详解】
选项A,连接,当与重合时,平面平面,此时直线与平面相交,A错误;
选项B,四边形为正方形,,当为的中点时,,
平面平面,
平面(平面),平面平面平面B正确;
选项C,在正方体中,
四边形为平行四边形,平面平面平面,点到平面的距离为定值,而的面积是定值,则三棱锥的体积为定值,正确;
选项D,平面,同理平面,且平面平面平面,又平面平面,D错误.
故选:BC.
12.ABD
【解析】对于选项在中,由正弦定理可得,即可判断出正误;对于选项在锐角中,由,可得,即可判断出正误;对于选项在中,由,利用正弦定理可得:,得到或即可判断出正误;对于选项在中,利用余弦定理可得:,代入已知可得,又,即可得到的形状,即可判断出正误.
【详解】对于,由,可得:,利用正弦定理可得:,正确;
对于,在锐角中,,,
,,
,因此不等式恒成立,正确;
对于,在中,由,利用正弦定理可得:,
,
,,
或,
或,
是等腰三角形或直角三角形,因此是假命题,错误.
对于,由于,,由余弦定理可得:,
可得,解得,可得,故正确.
故选:.
【点睛】本题考查正弦定理与余弦定理及三角形边角关系,主要涉及的考点是三角形内角的诱导公式的应用,同时考查正弦定理进行边角转化,属于中等题.
13.且
【分析】根据与的夹角为锐角,可得,且与不共线,然后建立关于的关系式,再求出的取值范围.
【详解】解:因为与的夹角为锐角,向量,
所以,且与不共线,
所以且,解得且,
所以的取值范围是且;
故答案为:且.
14.
【分析】设,根据正弦定理得出,,相除后化简即可得解.
【详解】设,则.
在中,,
在中,,
两式相除得,,
即,
因为,
所以可得,
所以.
故答案为:
15.16
【分析】根据球的体积为,求得球的半径,再由等腰直角三角形外接圆的圆心为线段的中点,求得,即为三棱锥的高,再由锥体的体积公式求解.
【详解】如图所示:
等腰直角三角形的直角边为,斜边,其外接圆的圆心为线段的中点,
所以是三棱锥的高,
设球的半径为,
因为,
所以,又,
所以,
所以三棱锥的体积为.
故答案为:16
16.或
【分析】由,解出A,B,C的正余弦值,将等式化简后代入,解出.
【详解】因为,,,,
所以,,,,
.
,
即,
所以,解得或.
故答案为:或.
17.(1)
(2)
【分析】(1)设,分别代入和,再根据两者均为实数可求得,,进而可求得复数z的共轭复数;
(2)化简,再根据复数对应的点在第三象限可建立不等式组,求解即可.
【详解】(1)设,则
由为实数,则,所以,
由为实数,则,所以
则,复数z的共轭复数.
(2)由(1)可知,
由对应的点在第三象限,得,即,
解得
故实数m的取值范围为
18.(1),最小正周期
(2)答案见解析
【解析】(1)
的最大值为2,
所以,最小正周期.
(2)
由(1)知,列表:
x 0
1 2 0 0 1
画图如下:
19.(1)
(2)
【分析】(1)根据圆柱的轴截面分析即可;
(2)直接利用球表面积、圆柱的侧面积公式计算即可.
【详解】(1)设圆柱的底面半径为R,小球的半径为r,且,
由圆柱与球的性质知,
即,
,
球A的体积为
(2)球B的表面积,
圆柱的侧面积,
圆柱的侧面积与球B的表面积之比为
20.(1),;
(2).
【分析】(1)由二倍角公式、两角差的正弦公式化函数为一个角的一个三角函数形式,
选①,由求得,再由正弦函数性质得单调增区间;选②,由结合正弦函数的最大值求得,再由正弦函数的单调性求得增区间;选③,由求得,再由正弦函数的单调性得增区间;
(2)求出的最大值,由可得参数范围.
【详解】(1)由条件知
若选①,则,解得,,
由,解得,,
所以函数的单调递增区间为.
若选②,则函数的最大值为,解得,,
由,解得,,
所以函数的单调递增区间为.
若选③,则,
所以,,
由,解得,,
所以函数的单调递增区间为.
(2)由题意可知只需即可.
当时,,所以,
因此函数的最大值为1.
令,则,则
当即时,函数的最大值为,于是,
整理得,解得,均满足,所以;
当即时,函数的最大值为,于是,无实解;
综上所述,实数m的取值范围为.
21.(1)证明见解析
(2)证明见解析
【分析】(1)取PC中点H,分别连接EH,FH,根据E,F,H分别为PD,AB,PC的中点,得到EAFH为平行四边形,从而EA∥FH,再利用线面平行的判定定理证明;
(2)根据E,G分别为PD,CD的中点,得到EG∥PC,利用线面平行的判定定理得到EG∥平面PCF,再利用面面平行的判定定理证明.
【详解】(1)证明:如图所示:
,
取PC中点H,分别连接EH,FH,
∵E,F,H分别为PD,AB,PC的中点,
∴,
∴EAFH为平行四边形.
∴EA∥FH.
又平面PCF,平面PCF,
∴AE∥平面PCF.
(2)∵E,G分别为PD,CD的中点,
∴EG∥PC.
又平面PCF,平面PCF,
∴EG∥平面PCF.
由(1)知AE∥平面PCF,EG∩AE=E.
∴平面PCF∥平面AEG.
22.(1)或
(2)
【分析】(1)由正弦定理化简可得,由可得,结合余弦定理得,换元求出其值,由正弦定理即可得答案;
(2)由得 ,结合余弦定理得,变形为,换元,可得,结合三角函数的性质可得不等式,即可求得答案.
【详解】(1)因为,由正弦定理得:,
即,即,
因为 ,所以,即,
由得:;
由得:,即,即,
由余弦定理可得:,
故,则,
令,则,解得 ,
由正弦定理得:,故的值为或;
(2)由得:,即,
由余弦定理可得:,
即,
故,
令,则,即,
由得,故,
故,即得 ,
故的取值范围是.
答案第1页,共2页
答案第1页,共2页
同课章节目录
