【黑龙江哈尔滨专版】2023届中考数学考向信息卷(含解析)
文档属性
| 名称 | 【黑龙江哈尔滨专版】2023届中考数学考向信息卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 21:23:10 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2023届中考数学考向信息卷
黑龙江哈尔滨专版
【满分:120】
一、选择题(本题共10题,每题3分,共30分)
1.-2022的倒数是( )
A.2022 B. C.-2022 D.
2.图中三视图对应的几何体是( )
A. B. C. D.
3.不等式组的解集是( )
A. B. C. D.
4.如图, 将两个含 角 的直角三角板ABC 和 放置在平面直角坐标系中, 两者 恰好是以O 为位似中心的位似图形, 且相似比为. 若点A,C 的坐标分别为,, 则 的长为( )
A. B. C. D.
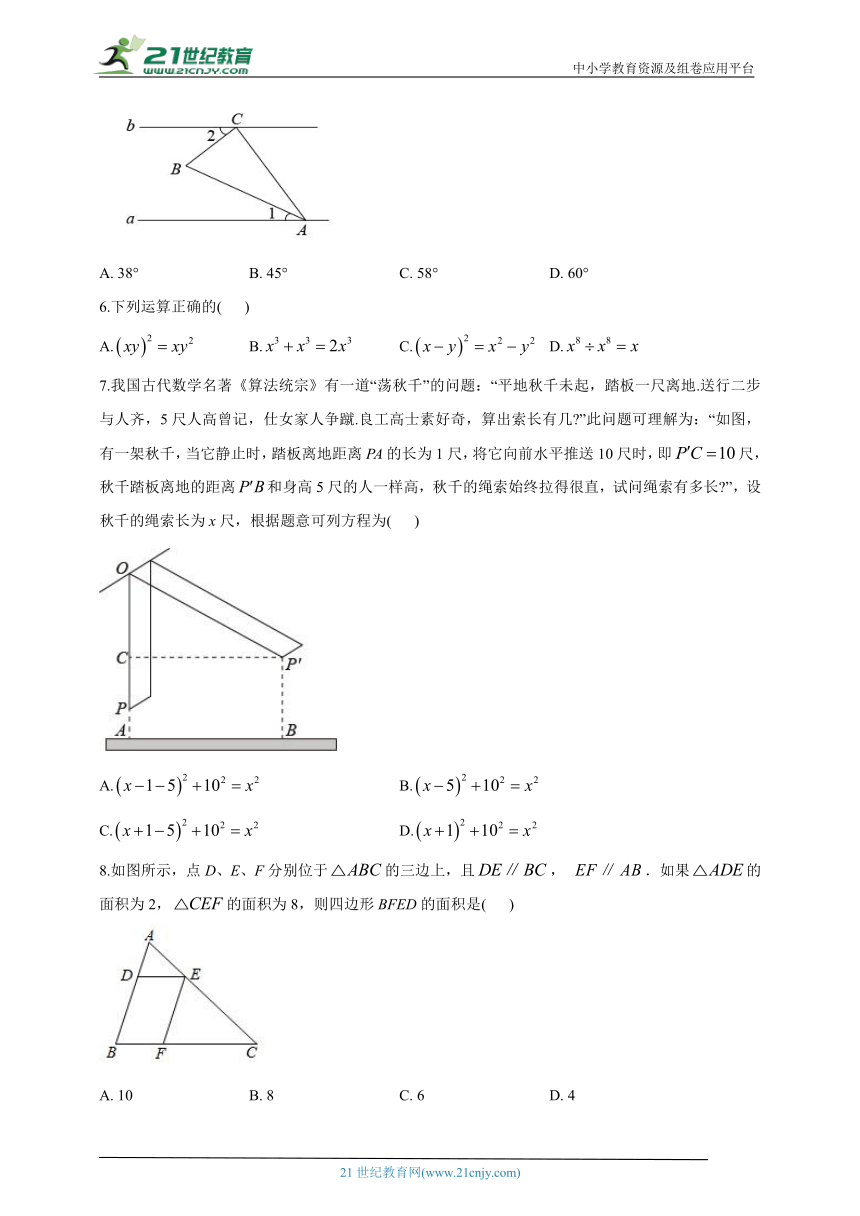
5.已知直线,将一块含30°角的直角三角板()按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若,则的度数是( )
A. 38° B. 45° C. 58° D. 60°
6.下列运算正确的( )
A. B. C. D.
7.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几 ”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长 ”,设秋千的绳索长为x尺,根据题意可列方程为( )
A. B.
C. D.
8.如图所示,点D、E、F分别位于的三边上,且, .如果的面积为2,的面积为8,则四边形BFED的面积是( )
A. 10 B. 8 C. 6 D. 4
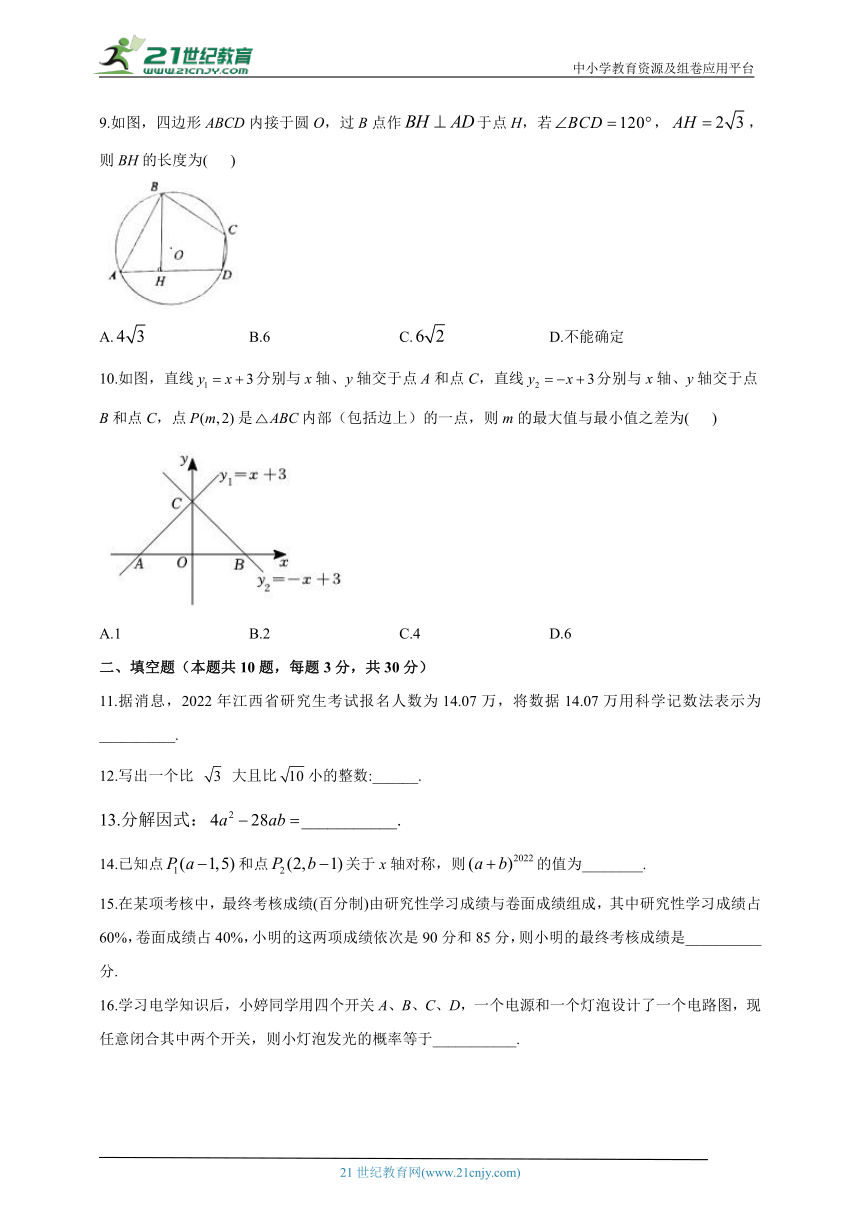
9.如图,四边形ABCD内接于圆O,过B点作于点H,若,,则BH的长度为( )
A. B.6 C. D.不能确定
10.如图,直线分别与x轴、y轴交于点A和点C,直线分别与x轴、y轴交于点B和点C,点是内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
二、填空题(本题共10题,每题3分,共30分)
11.据消息,2022年江西省研究生考试报名人数为14.07万,将数据14.07万用科学记数法表示为__________.
12.写出一个比 大且比小的整数:______.
13.分解因式:___________.
14.已知点和点关于x轴对称,则的值为________.
15.在某项考核中,最终考核成绩(百分制)由研究性学习成绩与卷面成绩组成,其中研究性学习成绩占60%,卷面成绩占40%,小明的这两项成绩依次是90分和85分,则小明的最终考核成绩是__________分.
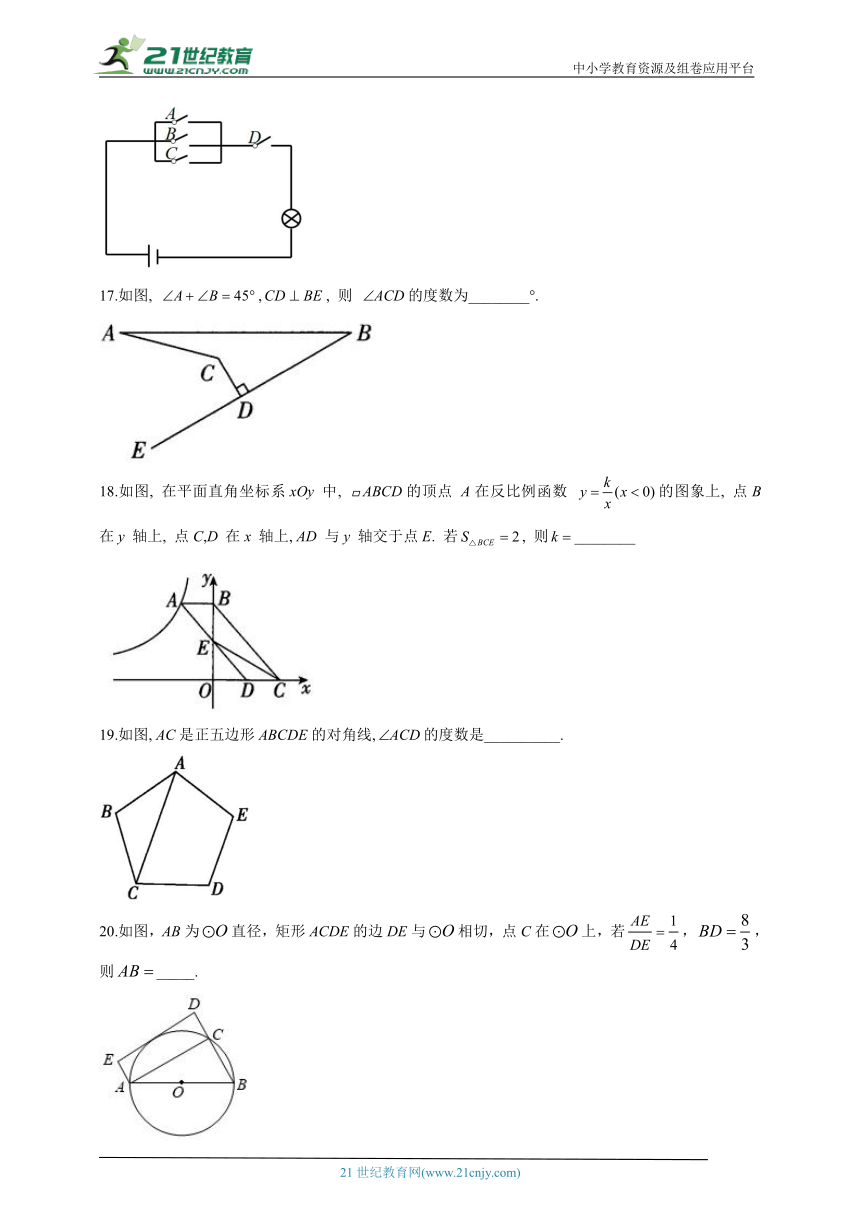
16.学习电学知识后,小婷同学用四个开关A、B、C、D,一个电源和一个灯泡设计了一个电路图,现任意闭合其中两个开关,则小灯泡发光的概率等于___________.
17.如图, ,, 则 的度数为________°.
18.如图, 在平面直角坐标系xOy 中, 的顶点 A在反比例函数 的图象上, 点B 在y 轴上, 点C,D 在x 轴上, AD 与y 轴交于点E. 若, 则________
19.如图, AC是正五边形ABCDE的对角线,的度数是__________.
20.如图,AB为直径,矩形ACDE的边DE与相切,点C在上,若,,则_____.
三、解答题(本题共7题,共60分)
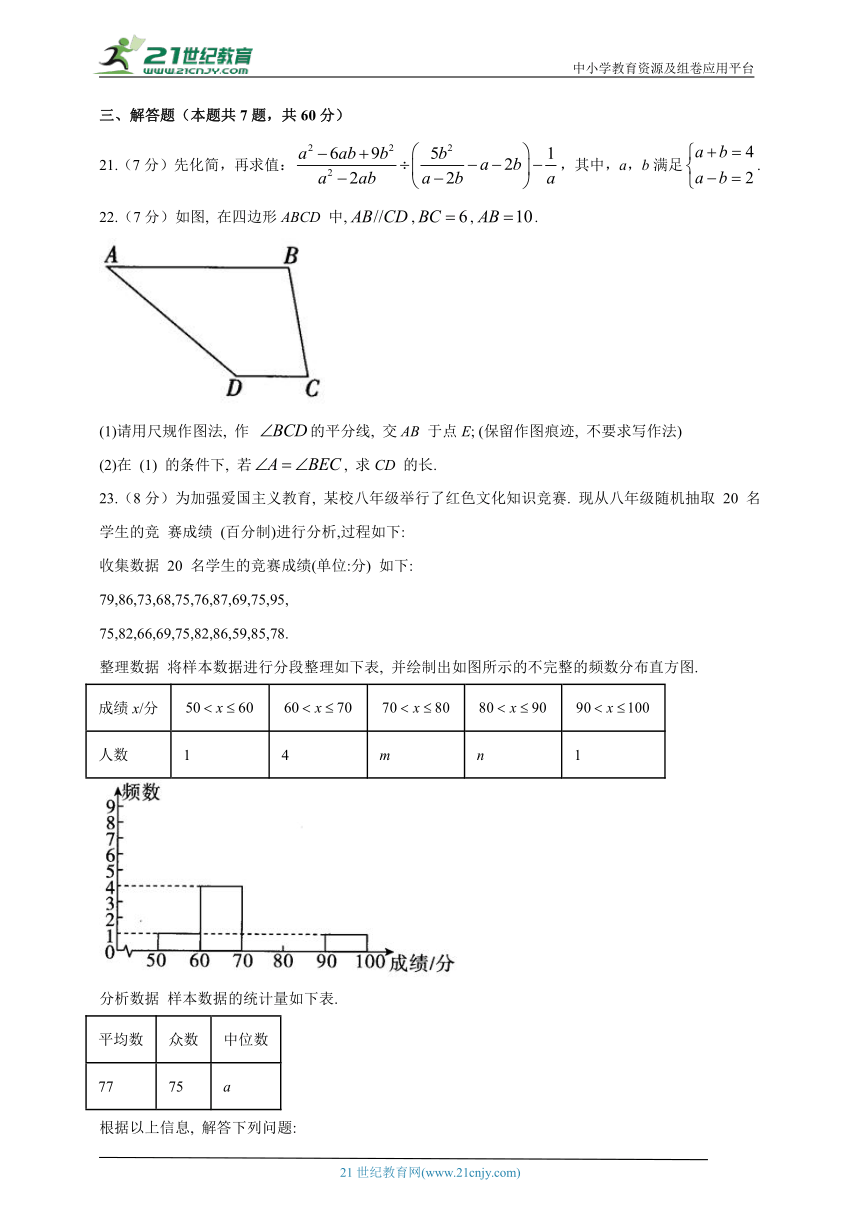
21.(7分)先化简,再求值:,其中,a,b满足.
22.(7分)如图, 在四边形ABCD 中,,,.
(1)请用尺规作图法, 作 的平分线, 交AB 于点E; (保留作图痕迹, 不要求写作法)
(2)在 (1) 的条件下, 若, 求CD 的长.
23.(8分)为加强爱国主义教育, 某校八年级举行了红色文化知识竞赛. 现从八年级随机抽取 20 名学生的竞 赛成绩 (百分制)进行分析,过程如下:
收集数据 20 名学生的竞赛成绩(单位:分) 如下:
79,86,73,68,75,76,87,69,75,95,
75,82,66,69,75,82,86,59,85,78.
整理数据 将样本数据进行分段整理如下表, 并绘制出如图所示的不完整的频数分布直方图.
成绩x/分
人数 1 4 m n 1
分析数据 样本数据的统计量如下表.
平均数 众数 中位数
77 75 a
根据以上信息, 解答下列问题:
(1)填空: _______,________.
(2)补全频数分布直方图.
(3)求a 的值, 并用一句话来概述数据a 的统计意义.
(4)若该校八年级共有 500 名学生, 试估计本次竞赛中成绩在 80 分以上的学生人数.
24.(8分)如图,AC是的直径,BC是的弦,点P是外一点,连接PB、AB,.
(1)求证:PB是的切线;
(2)连接OP,若,且,的半径为3,求BC的长.
25.(10分)2022 年4月,教育部印发《义务教育课程方案和课程标准 (2022年版)》, 将劳动从原来的综合实践活 动课程中独立出来. 某中学为了让学生体验农耕劳动, 开辟了一处耕种园, 需要采购一批菜苗开展种植活动. 据了解, 市场上每捆A 种菜苗的价格是菜苗基地的倍, 用 300 元在市场上购买的 A种菜苗 比在菜苗基地购买的少 3 捆.
(1)求菜苗基地每捆 A 种宷苗的价格.
(2)菜苗基地每捆 B 种菜苗的价格是 30 元. 学校决定在菜苗基地购买 A, B 两种菜苗共 100 捆, 且 A 种菜苗的捆数不超过 B 种菜苗的捆数. 菜苗基地为支持该校活动, 对 A, B 两种菜苗均提供九折优惠. 求本次购买最少花费多少钱.
26.(10分)如图1,在矩形ABCD中,,,把AB绕点B顺时针旋转得到,连接,过B点作于E点,交矩形ABCD边于F点.
(1)求的最小值;
(2)若A点所经过的路径长为,求点到直线AD的距离;
(3)如图2,若,求的值;
(4)当的度数取最大值时,直接写出CF的长.
27.(10分)如图, 已知点, 以点D 为顶点的抛物线 经过点A, 且与直线 交于点B,.
(1)求抛物线的表达式和点D 的坐标.
(2)在对称轴上存在一点M, 使得, 求出点M 的坐标.
(3)已知点P 为抛物线对称轴上一点, 点Q 为平面内一点, 是否存在以P,B,C,Q 为顶点的四边形是 菱形的情形 若存在, 直接写出点P 的坐标; 若不存在, 请说明理由.
答案以及解析
1.答案:B
解析:由于,所以-2022的倒数是,故选:B.
2.答案:C
解析:由主视图可以推出这个几何体是上下两个大小不同柱体,
从主视图推出这两个柱体的宽度不相同,
从俯视图推出上面是圆柱体,直径小于下面柱体的宽.
由此可以判断对应的几何体是选项B.故选B.
3.答案:D
解析:
解不等式①得: ,
解不等式②得: ,
不等式组的解集为 ,故D 正确.
故选: D.
4.答案:B
解析:由点A,C 的坐标分别为,, 可知,,
,.
5.答案: A
解析:如图,过点B作,
则
故选A
6.答案:B
解析:A.,故A选项计算错误,不符合题意;
B.,故B选项计算正确,符合题意;
C.,故C选项计算错误,不符合题意;
D.,故D选项计算错误,不符合题意.
故选:B.
7.答案:C
解析:由题意知:
,,,
在中,由勾股定理得:
.即.
故选:C.
8.答案: B
解析:,,
,,,
,
.
,
而,,
,
设,则,.
则,
设;
,
,
,
即,
解得:,
即四边形BFED面积为8.
故选:B.
9.答案:B
解析:四边形ABCD内接于,,
,
,,
,
故选:B.
10.答案:B
解析:点是内部(包括边上)的一点,
点P在直线上,如图所示,
当P为直线与直线的交点时,m取最大值,
当P为直线与直线的交点时,m取最小值,
中令,则,
中令,则,
m的最大值为1,m的最小值为-1.
则m的最大值与最小值之差为:.
故选:B.
11.答案:
解析:14.07万.
12.答案:2 (或3 )
解析:比,, 大且比 小的整数是 2 和 3 .
13.答案:
解析:原式.
故答案为:.
14.答案:1
解析:点和点关于x轴对称,
,
解得:,
.
故答案为:1.
15.答案:88
解析:解:小明的最终考核成绩是分,
故答案为:88.
16.答案:或0.5
解析:画树状图如下:
共有12种等可能的结果,其中小灯泡发光的结果有6种,
小灯泡发光的概率,
故答案为:.
17.答案:135
解析:如图 , 延长AC 交BE 于点F, 则
.
18.答案:-4
解析:过点 A作 轴于点 F,,,, 反比例 函数 的图象在第二象限, ,
19.答案:
解析:五边形ABCDE 是正五边形,
,
,,
20.答案:
解析:如图,过点O作直线相交AC于点G,DE于点F,
四边形ACDE是矩形,
且,且,.
,为直径,
,(梯形的中位线).
,
.
,,
,.
,即,
整理得,
解得(不符合题意).
.
故答案为:.
21.答案:
解析:原式=
.
解得.
当时,原式.
22.答案: (1)见解析
(2)4
解析:(1)如图, 射线CE 即为所求作的角平分线
(2) 由 (1) 知CE平分,
,
,
,
,
,
,
又,
四边形 AECD 为平行四边形
23.答案:(1)8,6
(2)见解析
(3) 75.5 分
(4) 175 名
解析:(1)略
(2)补全频数分布直方图如下.
(3)将该组数据按从小到大的顺序排列, 位于中间的 两个数据是 75,76 , 故.
a表示这 20 名学生中有 10 名学生的竞赛成绩高于 75.5 分.
(4)(名).
答:估计本次竞赛中成绩在 80 分以上的学生有175 名.
24.答案: (1)见解析
(2)
解析:证明:(1)连接OB,如图所示:
AC是的直径,
,
,
,
,
,
,
即,
PB是的切线;
(2)的半径为3,
,,
,
,
,
,
,
又,
,
,
即,
.
25.答案: (1)20元
(2) 2250元
解析:(1)设菜苗基地每捆A 种菜苗的价格为x 元,根据题意,得
解得,
经检验, 是原方程的解.
答:菜苗基地每捆A 种菜苗的价格为 20 元.
(2)设购买A 种菜苗 a捆, 则购买B 种菜苗 捆,根据题意, 得, 解得.
设本次购买花费w 元, 则.
,w随a 的增大而减小,
当时, w 有最小值,.
答: 本次购买最少花费2250元.
26.答案:(1)最小值为4
(2)点到直线AD的距离为3
(3)
(4)8或
解析:(1)连接BD,四边形ABCD是矩形,,
,,,
当点落在BD上时,最小,最小值为4.
(2)由题意得,,所以,
,是等边三角形,
,,
,过点作于M点,
,点到直线AD的距离为3.
(3),,,
,,
,,
,,
,过E作于H点,,
,,,
,.
27.答案: (1)
(2)
(3)存在, 点P的坐标为,, , 或
解析: (1) 将 代入, 得,
将 ,分别代入, 得
解得
故抛物线的表达式为.
抛物线的顶点D 的坐标为.
(2)易知抛物线的对称轴为直线, 且点A,C 关于 对称轴对称.
作直线AB, 交直线 于点M, 则点 M即为所求.
令,
解得,,
故.
设直线AB 的表达式为,
将 ,分别代入, 得
解得 故直线AB 的表达式为,
当 时, , 故.
(3)设,
易得 ,
①当 时,该四边形是以BC 为对角线的菱形, 则, 即, 解得,
点P 的坐标为.
②当 时,该四边形是以PC 为对角线的菱形, 则, 即, 解得, 故点P 的坐标为 或.
③当 时,该四边形是以 PB为对角线的菱形, 则, 即, 解得,
故点P 的坐标为 或.
综上可知, 点P 的坐标为,,,或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023届中考数学考向信息卷
黑龙江哈尔滨专版
【满分:120】
一、选择题(本题共10题,每题3分,共30分)
1.-2022的倒数是( )
A.2022 B. C.-2022 D.
2.图中三视图对应的几何体是( )
A. B. C. D.
3.不等式组的解集是( )
A. B. C. D.
4.如图, 将两个含 角 的直角三角板ABC 和 放置在平面直角坐标系中, 两者 恰好是以O 为位似中心的位似图形, 且相似比为. 若点A,C 的坐标分别为,, 则 的长为( )
A. B. C. D.
5.已知直线,将一块含30°角的直角三角板()按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若,则的度数是( )
A. 38° B. 45° C. 58° D. 60°
6.下列运算正确的( )
A. B. C. D.
7.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几 ”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长 ”,设秋千的绳索长为x尺,根据题意可列方程为( )
A. B.
C. D.
8.如图所示,点D、E、F分别位于的三边上,且, .如果的面积为2,的面积为8,则四边形BFED的面积是( )
A. 10 B. 8 C. 6 D. 4
9.如图,四边形ABCD内接于圆O,过B点作于点H,若,,则BH的长度为( )
A. B.6 C. D.不能确定
10.如图,直线分别与x轴、y轴交于点A和点C,直线分别与x轴、y轴交于点B和点C,点是内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
二、填空题(本题共10题,每题3分,共30分)
11.据消息,2022年江西省研究生考试报名人数为14.07万,将数据14.07万用科学记数法表示为__________.
12.写出一个比 大且比小的整数:______.
13.分解因式:___________.
14.已知点和点关于x轴对称,则的值为________.
15.在某项考核中,最终考核成绩(百分制)由研究性学习成绩与卷面成绩组成,其中研究性学习成绩占60%,卷面成绩占40%,小明的这两项成绩依次是90分和85分,则小明的最终考核成绩是__________分.
16.学习电学知识后,小婷同学用四个开关A、B、C、D,一个电源和一个灯泡设计了一个电路图,现任意闭合其中两个开关,则小灯泡发光的概率等于___________.
17.如图, ,, 则 的度数为________°.
18.如图, 在平面直角坐标系xOy 中, 的顶点 A在反比例函数 的图象上, 点B 在y 轴上, 点C,D 在x 轴上, AD 与y 轴交于点E. 若, 则________
19.如图, AC是正五边形ABCDE的对角线,的度数是__________.
20.如图,AB为直径,矩形ACDE的边DE与相切,点C在上,若,,则_____.
三、解答题(本题共7题,共60分)
21.(7分)先化简,再求值:,其中,a,b满足.
22.(7分)如图, 在四边形ABCD 中,,,.
(1)请用尺规作图法, 作 的平分线, 交AB 于点E; (保留作图痕迹, 不要求写作法)
(2)在 (1) 的条件下, 若, 求CD 的长.
23.(8分)为加强爱国主义教育, 某校八年级举行了红色文化知识竞赛. 现从八年级随机抽取 20 名学生的竞 赛成绩 (百分制)进行分析,过程如下:
收集数据 20 名学生的竞赛成绩(单位:分) 如下:
79,86,73,68,75,76,87,69,75,95,
75,82,66,69,75,82,86,59,85,78.
整理数据 将样本数据进行分段整理如下表, 并绘制出如图所示的不完整的频数分布直方图.
成绩x/分
人数 1 4 m n 1
分析数据 样本数据的统计量如下表.
平均数 众数 中位数
77 75 a
根据以上信息, 解答下列问题:
(1)填空: _______,________.
(2)补全频数分布直方图.
(3)求a 的值, 并用一句话来概述数据a 的统计意义.
(4)若该校八年级共有 500 名学生, 试估计本次竞赛中成绩在 80 分以上的学生人数.
24.(8分)如图,AC是的直径,BC是的弦,点P是外一点,连接PB、AB,.
(1)求证:PB是的切线;
(2)连接OP,若,且,的半径为3,求BC的长.
25.(10分)2022 年4月,教育部印发《义务教育课程方案和课程标准 (2022年版)》, 将劳动从原来的综合实践活 动课程中独立出来. 某中学为了让学生体验农耕劳动, 开辟了一处耕种园, 需要采购一批菜苗开展种植活动. 据了解, 市场上每捆A 种菜苗的价格是菜苗基地的倍, 用 300 元在市场上购买的 A种菜苗 比在菜苗基地购买的少 3 捆.
(1)求菜苗基地每捆 A 种宷苗的价格.
(2)菜苗基地每捆 B 种菜苗的价格是 30 元. 学校决定在菜苗基地购买 A, B 两种菜苗共 100 捆, 且 A 种菜苗的捆数不超过 B 种菜苗的捆数. 菜苗基地为支持该校活动, 对 A, B 两种菜苗均提供九折优惠. 求本次购买最少花费多少钱.
26.(10分)如图1,在矩形ABCD中,,,把AB绕点B顺时针旋转得到,连接,过B点作于E点,交矩形ABCD边于F点.
(1)求的最小值;
(2)若A点所经过的路径长为,求点到直线AD的距离;
(3)如图2,若,求的值;
(4)当的度数取最大值时,直接写出CF的长.
27.(10分)如图, 已知点, 以点D 为顶点的抛物线 经过点A, 且与直线 交于点B,.
(1)求抛物线的表达式和点D 的坐标.
(2)在对称轴上存在一点M, 使得, 求出点M 的坐标.
(3)已知点P 为抛物线对称轴上一点, 点Q 为平面内一点, 是否存在以P,B,C,Q 为顶点的四边形是 菱形的情形 若存在, 直接写出点P 的坐标; 若不存在, 请说明理由.
答案以及解析
1.答案:B
解析:由于,所以-2022的倒数是,故选:B.
2.答案:C
解析:由主视图可以推出这个几何体是上下两个大小不同柱体,
从主视图推出这两个柱体的宽度不相同,
从俯视图推出上面是圆柱体,直径小于下面柱体的宽.
由此可以判断对应的几何体是选项B.故选B.
3.答案:D
解析:
解不等式①得: ,
解不等式②得: ,
不等式组的解集为 ,故D 正确.
故选: D.
4.答案:B
解析:由点A,C 的坐标分别为,, 可知,,
,.
5.答案: A
解析:如图,过点B作,
则
故选A
6.答案:B
解析:A.,故A选项计算错误,不符合题意;
B.,故B选项计算正确,符合题意;
C.,故C选项计算错误,不符合题意;
D.,故D选项计算错误,不符合题意.
故选:B.
7.答案:C
解析:由题意知:
,,,
在中,由勾股定理得:
.即.
故选:C.
8.答案: B
解析:,,
,,,
,
.
,
而,,
,
设,则,.
则,
设;
,
,
,
即,
解得:,
即四边形BFED面积为8.
故选:B.
9.答案:B
解析:四边形ABCD内接于,,
,
,,
,
故选:B.
10.答案:B
解析:点是内部(包括边上)的一点,
点P在直线上,如图所示,
当P为直线与直线的交点时,m取最大值,
当P为直线与直线的交点时,m取最小值,
中令,则,
中令,则,
m的最大值为1,m的最小值为-1.
则m的最大值与最小值之差为:.
故选:B.
11.答案:
解析:14.07万.
12.答案:2 (或3 )
解析:比,, 大且比 小的整数是 2 和 3 .
13.答案:
解析:原式.
故答案为:.
14.答案:1
解析:点和点关于x轴对称,
,
解得:,
.
故答案为:1.
15.答案:88
解析:解:小明的最终考核成绩是分,
故答案为:88.
16.答案:或0.5
解析:画树状图如下:
共有12种等可能的结果,其中小灯泡发光的结果有6种,
小灯泡发光的概率,
故答案为:.
17.答案:135
解析:如图 , 延长AC 交BE 于点F, 则
.
18.答案:-4
解析:过点 A作 轴于点 F,,,, 反比例 函数 的图象在第二象限, ,
19.答案:
解析:五边形ABCDE 是正五边形,
,
,,
20.答案:
解析:如图,过点O作直线相交AC于点G,DE于点F,
四边形ACDE是矩形,
且,且,.
,为直径,
,(梯形的中位线).
,
.
,,
,.
,即,
整理得,
解得(不符合题意).
.
故答案为:.
21.答案:
解析:原式=
.
解得.
当时,原式.
22.答案: (1)见解析
(2)4
解析:(1)如图, 射线CE 即为所求作的角平分线
(2) 由 (1) 知CE平分,
,
,
,
,
,
,
又,
四边形 AECD 为平行四边形
23.答案:(1)8,6
(2)见解析
(3) 75.5 分
(4) 175 名
解析:(1)略
(2)补全频数分布直方图如下.
(3)将该组数据按从小到大的顺序排列, 位于中间的 两个数据是 75,76 , 故.
a表示这 20 名学生中有 10 名学生的竞赛成绩高于 75.5 分.
(4)(名).
答:估计本次竞赛中成绩在 80 分以上的学生有175 名.
24.答案: (1)见解析
(2)
解析:证明:(1)连接OB,如图所示:
AC是的直径,
,
,
,
,
,
,
即,
PB是的切线;
(2)的半径为3,
,,
,
,
,
,
,
又,
,
,
即,
.
25.答案: (1)20元
(2) 2250元
解析:(1)设菜苗基地每捆A 种菜苗的价格为x 元,根据题意,得
解得,
经检验, 是原方程的解.
答:菜苗基地每捆A 种菜苗的价格为 20 元.
(2)设购买A 种菜苗 a捆, 则购买B 种菜苗 捆,根据题意, 得, 解得.
设本次购买花费w 元, 则.
,w随a 的增大而减小,
当时, w 有最小值,.
答: 本次购买最少花费2250元.
26.答案:(1)最小值为4
(2)点到直线AD的距离为3
(3)
(4)8或
解析:(1)连接BD,四边形ABCD是矩形,,
,,,
当点落在BD上时,最小,最小值为4.
(2)由题意得,,所以,
,是等边三角形,
,,
,过点作于M点,
,点到直线AD的距离为3.
(3),,,
,,
,,
,,
,过E作于H点,,
,,,
,.
27.答案: (1)
(2)
(3)存在, 点P的坐标为,, , 或
解析: (1) 将 代入, 得,
将 ,分别代入, 得
解得
故抛物线的表达式为.
抛物线的顶点D 的坐标为.
(2)易知抛物线的对称轴为直线, 且点A,C 关于 对称轴对称.
作直线AB, 交直线 于点M, 则点 M即为所求.
令,
解得,,
故.
设直线AB 的表达式为,
将 ,分别代入, 得
解得 故直线AB 的表达式为,
当 时, , 故.
(3)设,
易得 ,
①当 时,该四边形是以BC 为对角线的菱形, 则, 即, 解得,
点P 的坐标为.
②当 时,该四边形是以PC 为对角线的菱形, 则, 即, 解得, 故点P 的坐标为 或.
③当 时,该四边形是以 PB为对角线的菱形, 则, 即, 解得,
故点P 的坐标为 或.
综上可知, 点P 的坐标为,,,或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
