圆周角

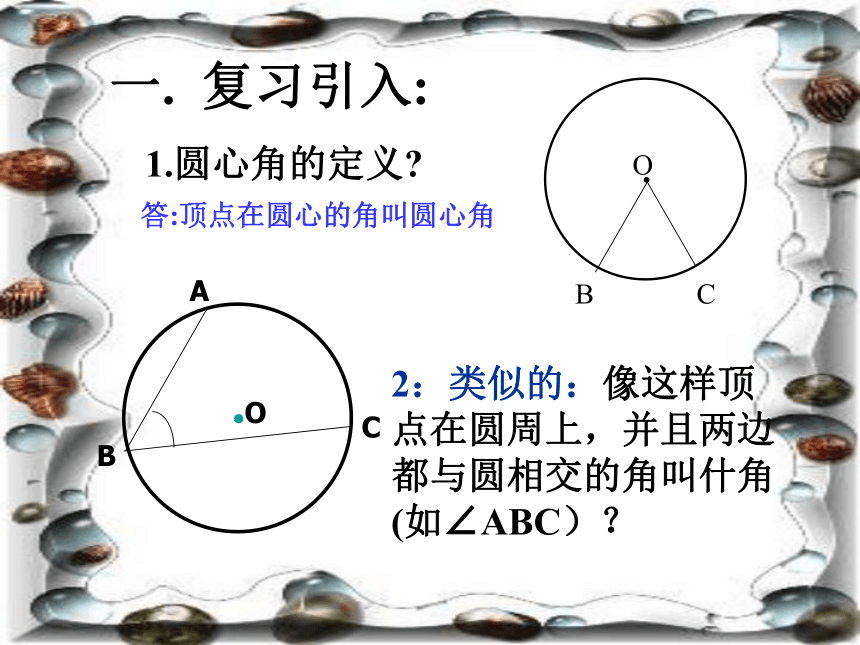
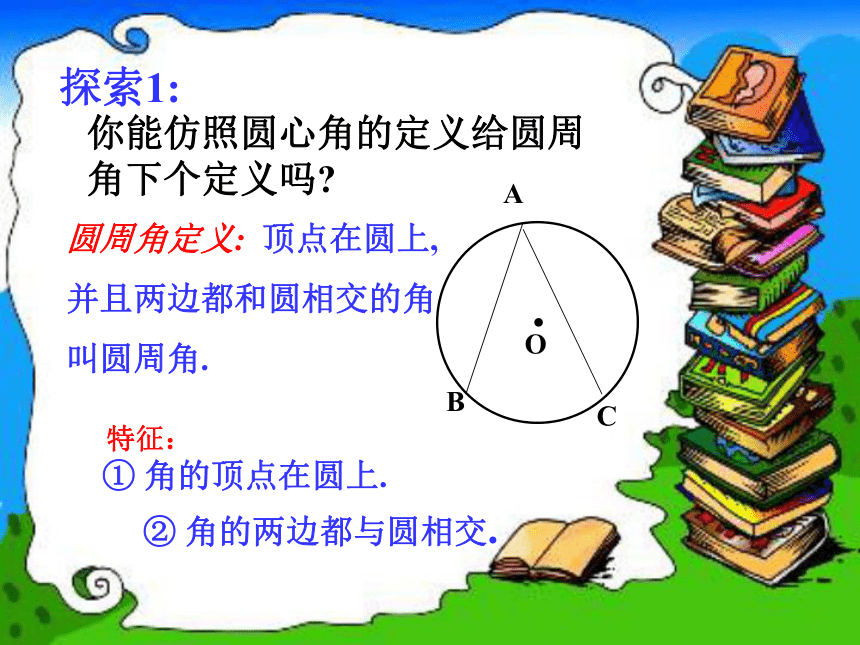
课件19张PPT。24.1.4 圆周角一. 复习引入:1.圆心角的定义?答:顶点在圆心的角叫圆心角2：类似的：像这样顶点在圆周上，并且两边都与圆相交的角叫什角(如∠ABC）？探索1:你能仿照圆心角的定义给圆周角下个定义吗?特征：① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
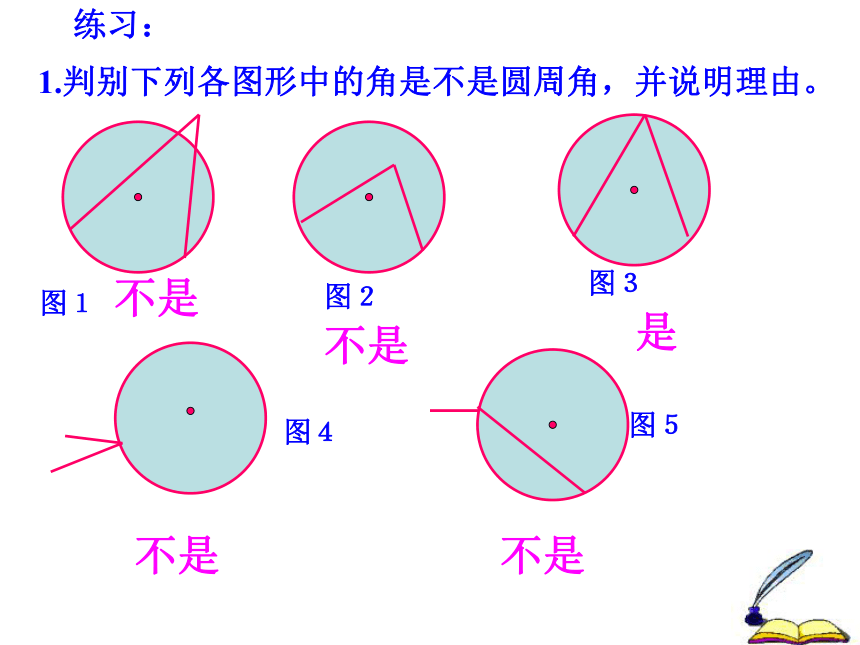
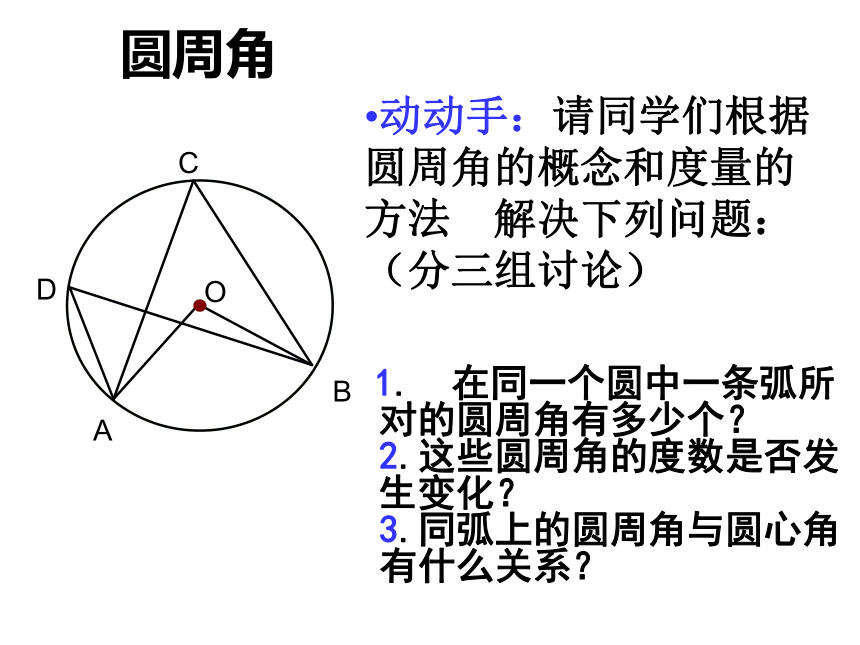
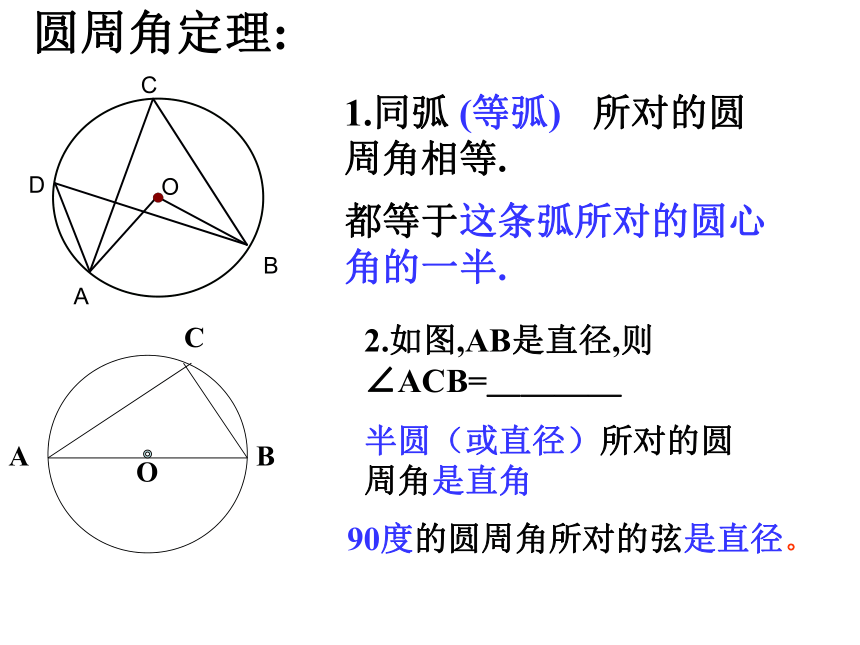
叫圆周角.练习：1.判别下列各图形中的角是不是圆周角，并说明理由。不是不是是不是不是图１图２图３图４图５圆周角 1. 在同一个圆中一条弧所 对的圆周角有多少个？ 2.这些圆周角的度数是否发生变化？ 3.同弧上的圆周角与圆心角有什么关系？动动手：请同学们根据圆周角的概念和度量的方法 解决下列问题：（分三组讨论） 1.同弧 所对的圆周角相等.(等弧)2.如图,AB是直径,则∠ACB=＿＿＿＿
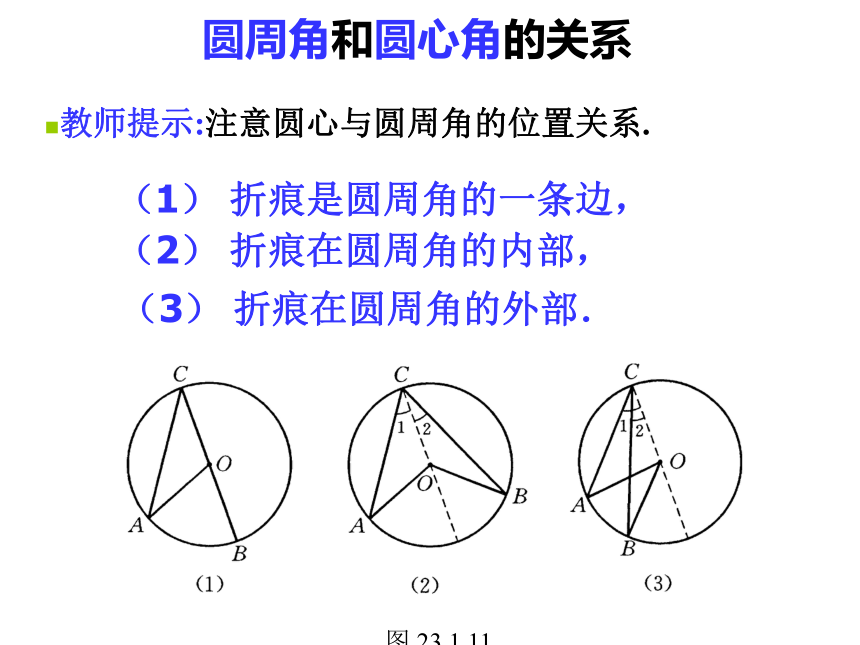
半圆（或直径）所对的圆周角是直角都等于这条弧所对的圆心角的一半.圆周角定理: 90度的圆周角所对的弦是直径。圆周角和圆心角的关系教师提示:注意圆心与圆周角的位置关系.（1） 折痕是圆周角的一条边， （2） 折痕在圆周角的内部， （3） 折痕在圆周角的外部． 圆周角和圆心角的关系证明1.首先考虑一种特殊情况：
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角，∴∠AOC=∠B+∠A.∵OA=OB，∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.老师期望:你可要理解并掌握这个模型.2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,圆周角和圆心角的关系圆周角和圆心角的关系3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC = ∠AOC.∠ABD = ∠AOD,∠CBD = ∠COD,综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:同弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.牛刀小试1.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8牛刀小试2：已知⊙O中弦AB的等于半径，
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。牛刀小试3.如图，∠A是圆O的圆周角， ∠A=40°，求∠OBC的度数。 拓展4.例: 如图，AB是⊙O的直径AB=10cm,
弦AC=6cm,∠ACB的平分线交⊙O于点D . 求 BC, AD ,BD 的长.106我能行练习1:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.40° 这节课你有什么收获和体会，和大家一起分享一下吧！一 、这节课主要学习了两个知识点：
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。总结扩展：三、圆周角及圆周角定理的应用极其广泛，也是中考的一个重要考点，望同学们灵活运用