【名师点拨】2014-2015学年湘教版九年级数学上册过关自测卷:第1章一元二次方程(含答案)
文档属性
| 名称 | 【名师点拨】2014-2015学年湘教版九年级数学上册过关自测卷:第1章一元二次方程(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-29 10:49:28 | ||
图片预览




文档简介
第1章过关自测卷
(90分钟 100分)
一、选择题(每题3分,共21分)
1.(2013,河南)函数y=(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的( )
A.第一、三象限 B.第三、四象限
C.第一、二象限 D.第二、四象限
2.下列各点中,在函数y=-的图象上的点是( )
A.(-2,-4) B.(2,3) C.( -6,1) D.(-,3)
3. 反比例函数y=的图象位于第二、四象限,则k的取值范围是( )
A.k> B.k< C.k= D.不存在
4. 函数y=-kx与y=(k≠0)的图象的交点个数是( )
A.0 B.1 C.2 D.不确定
5. 在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当<0<时,有<,则m的取值范围是( )
A.m<0 B.m>0 C.m< D.m>
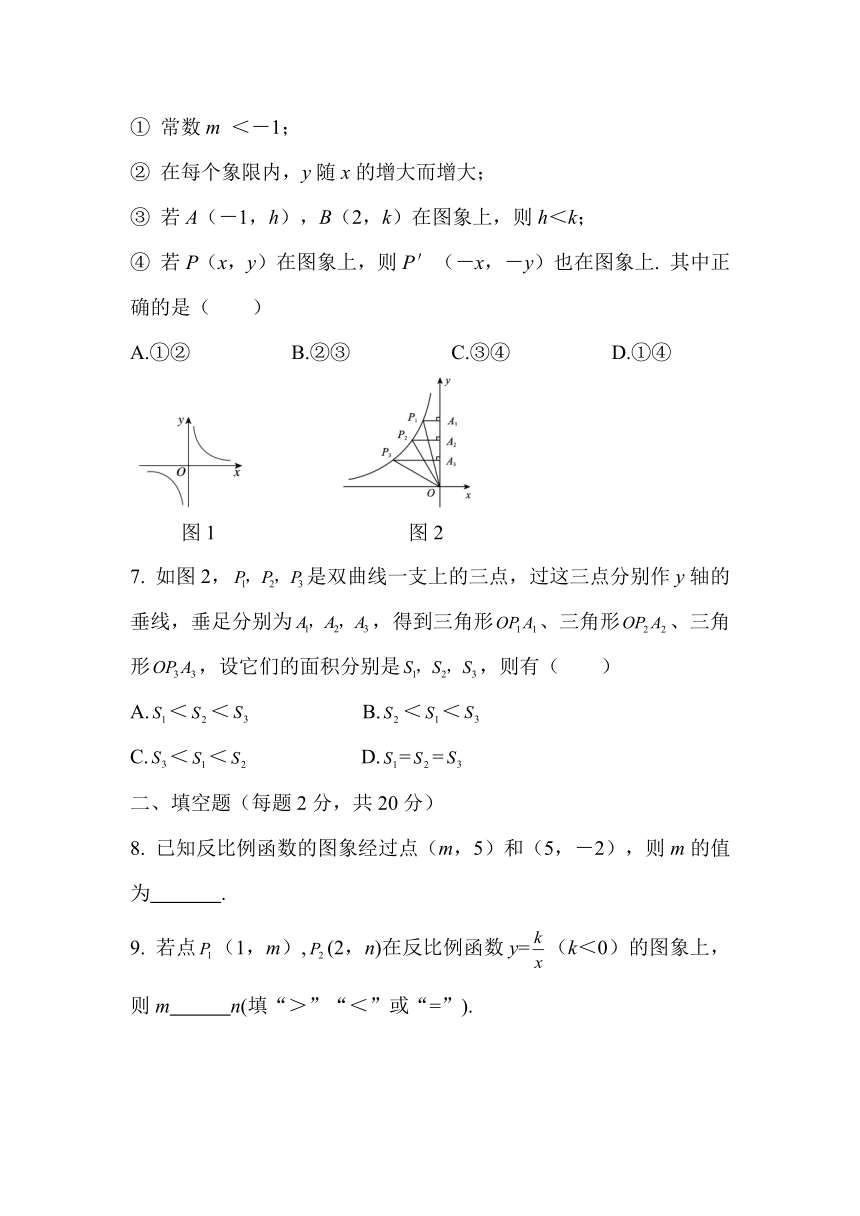
6.(2013,河北)反比例函数y=的图象如图1所示,以下结论:
① 常数m <-1;
② 在每个象限内,y随x的增大而增大;
③ 若A(-1,h),B(2,k)在图象上,则h<k;
④ 若P(x,y)在图象上,则P′(-x,-y)也在图象上. 其中正确的是( )
A.①② B.②③ C.③④ D.①④
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2
7. 如图2,是双曲线一支上的三点,过这三点分别作y轴的垂线,垂足分别为,得到三角形、三角形、三角形,设它们的面积分别是,则有( )
A.<< B.<<
C.<< D.==
二、填空题(每题2分,共20分)
8. 已知反比例函数的图象经过点(m,5)和(5,-2),则m的值为 .
9. 若点(1,m),(2,n)在反比例函数y=(k<0)的图象上,则m n(填“>”“<”或“=”).
10. 已知反比例函数y=(k≠0)的图象经过点P(-2,1),则这个函数的图象位于第 象限.
11. 矩形的面积是12 cm ,则一边长y(cm)与其邻边的长x(cm)之间的函数关系式为 .
12.(2013,达州)点(),()在反比例函数y=的图象上,当<<0时,<,则k的取值可以是 (只填一个符合条件的k的值).
13. 若一次函数y=kx+b与反比例函数y=的图象交于点(2,2),则k= ,b= .
14. 若函数y=4x与y=的图象有一交点,其坐标是(,2),则另一交点坐标是 .
15. 某种蓄电池的电压为定值,使用此电 ( http: / / www.21cnjy.com )源时,电流 I(A)与可变电阻 R(Ω)之间的函数关系如图3所示,当用电器的电流为1.5A时,用电器的可变电阻为 Ω.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图3 图4 图5
16.(2013,张家界)如图4,直线x=2与反比例函数y=和y=-的图象分别交于A,B两点,若点P是y轴上任意一点,则△PAB的面积是 .
17. 两个反比例函数y=,y=在第一象限内的图象如图5, 点,在反比例函数y=的图象上,它们的横坐标分别是,纵坐标分别是1,3,5,…,4 029,共2 015个连续奇数,过点分别作y轴的平行线,与y=的图象交点依次是(),(),(),…,(),则= .
三、解答题(19~21题每题6分,24,25题每题10分,其余每题7分,共59分)
18. 在图6所示的坐标系中,画出y=和y= 2x的图象,并求出交点坐标.
( http: / / www.21cnjy.com )
图6
19. 已知反比例函数y=的图象过点A(x,y),且点A的坐标满足
(x+5) +=0,求此反比例函数的表达式.
20. 某学校计划建一块面积为600 m 的长方形草坪.
(1)草坪的长y (单位:m)与宽x(单位:m)的函数关系式是什么
(2)如果把草坪的长与宽的比定为3∶2,则草坪的长与宽分别为多少
21. 某商场出售一批名牌衬衣,进价为80 ( http: / / www.21cnjy.com )元/件,在营销中发现,该衬衣的日销售量y(件)是售价x(元/件)的反比例函数,且当售价定为100元/件时,每天可售出30件.
(1)请求出y与x之间的函数关系式(不必写出自变量的取值范围);
(2)若要使日销售利润达到2 040元,则每件售价应定为多少元?
22.(2013,衢州)如图7,函数=-x+4的图象与函数=(x>0)的图象交于A(a,1),B(1,b)两点.
(1)求函数=的表达式;
( http: / / www.21cnjy.com )
图7
(2)观察图象,比较当x>0时,与的大小.
23. 如图8,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数与一次函数的表达式;
( http: / / www.21cnjy.com )
图8
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求方程kx+b- =0的解(请直接写出答案);
(4)求不等式kx+b-<0的解集(请直接写出答案).
24. 水产公司有一种海产品共2 104 kg,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x (元/kg) 400 250 240 200 150 125 120
销售量y (kg) 30 40 48 60 80 96 100
观察表中数据,发现可以用反比例函数表达这种 ( http: / / www.21cnjy.com )海产品每天的销售量y(kg)与售价x(元/kg)之间的关系.现假定在这批海产品的销售中,每天的销售量y(kg)与售价x(元/kg)之间都满足这一关系.
(1)写出这个反比例函数的表达式(不考虑自变量的取值范围),并补全表格;
(2)在试销8天后,公司决 ( http: / / www.21cnjy.com )定将这种海产品的售价定为150元/kg,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)按(2)中定价继续销售15天后, ( http: / / www.21cnjy.com )公司发现剩余的这些海产品必须在2天内全部售出,此时需要重新确定一个销售价格,使在以后的销售过程中都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
25. 一次函数y=ax+b的图象分别与x轴、y轴交于点M,N,与反比例函数y= (k>0)的图象交于点A(),B().过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图9 图10
(1)若点A,B在反比例函数y=(k>0)的图象的同一分支上,如图9,试证明:①;②AN=BM;
(2)若点A,B分别在反比例函数y= (k>0)的图象的不同分支上,如图10,则AN与BM还相等吗?试证明你的结论.
参考答案及点拨
一、1.D 2.C 3.B
4.A 点拨:当k>0时,y=-kx的图象经过第二、四象限,y=的图象在第一、三象限,无交点;当k<0时,y=-kx的图象经过第一、三象限,y=的图象在第二、四象限,无交点.故交点个数为0.
5.C
6.C 点拨:由于函数图象在第一、三象限,故有m>0,①错误;在每个象限内,y随x的增大而减小,故②错误;将A,B坐标代入,得:h=-m,k=,因为m>0,所以h<k,故③正确;函数图象关于原点对称,故④正确.
7.D 点拨:考查反比例函数比例系数k的几何意义.
二、8.-2 9.< 10.二、四 11.y=(x>0)
12.-1 点拨:此题答案不唯一,k为负数均可.
13.4;-6 14. (-,-2)
15. 24 点拨:由题图设函数关系式为I=,将(9,4)代入,得U=36,故I=,当I=1.5时,R=24.
16. 点拨:把x=2分别代入y=,y=-,得y=1,y=-.∴A(2,1),B(2,-),∴AB=1-(-)=.∵P为y轴上的任意一点,∴点P到直线x=2的距离为2,∴△PAB的面积=AB×2=.
17. 点拨:对于y=,当y=4 029时,x2 015=.对于y=,∵x2 015=,∴y2 015=.
三、18.解:图象如答图1;
观察图象可知,交点坐标为A(1,2),B(-1,-2).
( http: / / www.21cnjy.com )
答图1
19.解:由(x+5)2+ =0,可得 解得
所以点A的坐标为(-5,6).
又因为点A在反比例函数y=的图象上,所以将点A(-5,6)的坐标代入y=,得6=,所以k=-30,故此反比例函数的表达式为y=-.
点拨:解此题的关键在于明白(x+5)2+ =0表示的意义.因为(x+5)2≥0且≥0,要使(x+5)2+ =0,则必须使x+5=0且y-6=0.
20.解:(1)依题意得xy=600,∴y=(0<x<). (2)由y∶x=3∶2,得3x=2y,∴y=,∴x2=600,解得x=20(负值舍去).当x=20时,y=30.∴草坪的长与宽分别是30 m和20 m.
21.解:(1)设y= (k≠0),把x=100,y=30代入y=,得k=3 000,所以y与x之间的函数关系式为y=.
(2)由题意,得(x-80)·y=2 040,即(x-80)·=2 040,解得x=250,经检验x=250是原方程的根,且符合题意.所以每件售价应定为250元.
点拨:(2)中列出的方程为分式方程,得出解后应进行检验.
22.解:(1)把点A的坐标(a,1)代入y1=-x+4,得-a+4=1,解得:a=3,
∴点A的坐标为(3,1).把点A的坐标代入y2=,得k=3,∴函数y2=的表达式为:y2=.
(2)易得b=3,所以由图象可知,当0<x<1或x>3时,y1<y2;当x=1或x=3时,y1= y2 ;当1<x<3时,y1>y2.
23.解:(1)∵B是反比例函数y=图象上的一点,∴把B(2,-4)的坐标代入y=,得-4=,解得m=-8,∴反比例函数的表达式是y=-.把A(-4,n)的坐标代入y=-,得n=-=2,∴点A的坐标为(-4,2).∵点A,B都在一次函数y=kx+b的图象上,∴把A,B两点的坐标分别代入y=kx+b,得解得
∴一次函数的表达式是y=-x-2.
(2)∵点C在x轴上,∴它的纵坐标为0,把y=0代入y=-x-2,得0=-x-2,∴x=-2,∴点C的坐标为(-2,0). ∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=2+4=6.
(3)x=-4或x=2.
(4)-4<x<0或x>2.
24.解:(1)设这个反比例函数的表达式为y=.将x=400,y=30代入y=,解得k=12 000.所以所求反比例函数的表达式为y=.
补全表格如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x(元/ kg) 400 300 250 240 200 150 125 120
销售量y(kg) 30 40 48 50 60 80 96 100
(2)2 104-(30+40+4 ( http: / / www.21cnjy.com )8+50+60+80+96+100)=1 600(kg),即8天试销后,余下的海产品还有1 600 kg.
当x=150时,y=80,1 600÷80=20(天),即余下的这些海产品预计再用20天可以全部售出.
(3)1 600-80×15=400(kg),400÷2=200(kg),即如果正好用2天售完,那么每天需要售出200 kg.当y=200时,x==60,即新确定的价格最高不超过每千克60元才能完成销售任务.
25.(1)证明:①因为AC⊥x轴,AE⊥y轴,所以四边形AEOC为矩形.
因为BF⊥x轴,BD⊥y轴,所以四边形BDOF为矩形.
因为AC⊥x轴,BD⊥y轴,
所以四边形AEDK、四边形DOCK、四边形CFBK均为矩形.
因为OC=x1,AC=y1, x1·y1=k, 所以S矩形AEOC =OC·AC=x1·y1=k.
因为OF=x2,BF=y2,x2·y2=k,所以S矩形BDOF=OF·FB=x2·y2=k,
所以S矩形AEOC=S矩形BDOF.
因为S矩形AEDK=S矩形AEOC- S矩形DOCK,S矩形CFBK=S矩形BDOF-S矩形DOCK,所以S矩形AEDK=S矩形CFBK.
②由①知S矩形AEDK=S矩形CFBK,所以AK·DK=BK·CK.
所以=.又因为∠AKB=∠CKD,所以△ABK∽△CDK,
所以∠ABK=∠CDK,所以AB∥CD.
因为AC∥y轴,所以四边形ACDN是平行四边形,所以AN=CD,同理BM=CD.所以AN=BM.
(2)解:AN与BM仍然相等.
证明:因为S矩形AEDK=S矩形AEOC+S矩形ODKC,
S矩形BKCF=S矩形BDOF+S矩形ODKC,S矩形AEOC=S矩形BDOF=k,
所以S矩形AEDK=S矩形BKCF,所以AK·DK=BK·CK,所以=.
又因为∠K=∠K,所以△CDK∽△ ( http: / / www.21cnjy.com )ABK.所以∠CDK=∠ABK.所以AB∥CD.因为AC∥y轴,所以四边形ANDC是平行四边形,所以AN=CD.同理BM=CD,所以AN=BM.
(90分钟 100分)
一、选择题(每题3分,共21分)
1.(2013,河南)函数y=(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的( )
A.第一、三象限 B.第三、四象限
C.第一、二象限 D.第二、四象限
2.下列各点中,在函数y=-的图象上的点是( )
A.(-2,-4) B.(2,3) C.( -6,1) D.(-,3)
3. 反比例函数y=的图象位于第二、四象限,则k的取值范围是( )
A.k> B.k< C.k= D.不存在
4. 函数y=-kx与y=(k≠0)的图象的交点个数是( )
A.0 B.1 C.2 D.不确定
5. 在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当<0<时,有<,则m的取值范围是( )
A.m<0 B.m>0 C.m< D.m>
6.(2013,河北)反比例函数y=的图象如图1所示,以下结论:
① 常数m <-1;
② 在每个象限内,y随x的增大而增大;
③ 若A(-1,h),B(2,k)在图象上,则h<k;
④ 若P(x,y)在图象上,则P′(-x,-y)也在图象上. 其中正确的是( )
A.①② B.②③ C.③④ D.①④
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2
7. 如图2,是双曲线一支上的三点,过这三点分别作y轴的垂线,垂足分别为,得到三角形、三角形、三角形,设它们的面积分别是,则有( )
A.<< B.<<
C.<< D.==
二、填空题(每题2分,共20分)
8. 已知反比例函数的图象经过点(m,5)和(5,-2),则m的值为 .
9. 若点(1,m),(2,n)在反比例函数y=(k<0)的图象上,则m n(填“>”“<”或“=”).
10. 已知反比例函数y=(k≠0)的图象经过点P(-2,1),则这个函数的图象位于第 象限.
11. 矩形的面积是12 cm ,则一边长y(cm)与其邻边的长x(cm)之间的函数关系式为 .
12.(2013,达州)点(),()在反比例函数y=的图象上,当<<0时,<,则k的取值可以是 (只填一个符合条件的k的值).
13. 若一次函数y=kx+b与反比例函数y=的图象交于点(2,2),则k= ,b= .
14. 若函数y=4x与y=的图象有一交点,其坐标是(,2),则另一交点坐标是 .
15. 某种蓄电池的电压为定值,使用此电 ( http: / / www.21cnjy.com )源时,电流 I(A)与可变电阻 R(Ω)之间的函数关系如图3所示,当用电器的电流为1.5A时,用电器的可变电阻为 Ω.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图3 图4 图5
16.(2013,张家界)如图4,直线x=2与反比例函数y=和y=-的图象分别交于A,B两点,若点P是y轴上任意一点,则△PAB的面积是 .
17. 两个反比例函数y=,y=在第一象限内的图象如图5, 点,在反比例函数y=的图象上,它们的横坐标分别是,纵坐标分别是1,3,5,…,4 029,共2 015个连续奇数,过点分别作y轴的平行线,与y=的图象交点依次是(),(),(),…,(),则= .
三、解答题(19~21题每题6分,24,25题每题10分,其余每题7分,共59分)
18. 在图6所示的坐标系中,画出y=和y= 2x的图象,并求出交点坐标.
( http: / / www.21cnjy.com )
图6
19. 已知反比例函数y=的图象过点A(x,y),且点A的坐标满足
(x+5) +=0,求此反比例函数的表达式.
20. 某学校计划建一块面积为600 m 的长方形草坪.
(1)草坪的长y (单位:m)与宽x(单位:m)的函数关系式是什么
(2)如果把草坪的长与宽的比定为3∶2,则草坪的长与宽分别为多少
21. 某商场出售一批名牌衬衣,进价为80 ( http: / / www.21cnjy.com )元/件,在营销中发现,该衬衣的日销售量y(件)是售价x(元/件)的反比例函数,且当售价定为100元/件时,每天可售出30件.
(1)请求出y与x之间的函数关系式(不必写出自变量的取值范围);
(2)若要使日销售利润达到2 040元,则每件售价应定为多少元?
22.(2013,衢州)如图7,函数=-x+4的图象与函数=(x>0)的图象交于A(a,1),B(1,b)两点.
(1)求函数=的表达式;
( http: / / www.21cnjy.com )
图7
(2)观察图象,比较当x>0时,与的大小.
23. 如图8,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数与一次函数的表达式;
( http: / / www.21cnjy.com )
图8
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求方程kx+b- =0的解(请直接写出答案);
(4)求不等式kx+b-<0的解集(请直接写出答案).
24. 水产公司有一种海产品共2 104 kg,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x (元/kg) 400 250 240 200 150 125 120
销售量y (kg) 30 40 48 60 80 96 100
观察表中数据,发现可以用反比例函数表达这种 ( http: / / www.21cnjy.com )海产品每天的销售量y(kg)与售价x(元/kg)之间的关系.现假定在这批海产品的销售中,每天的销售量y(kg)与售价x(元/kg)之间都满足这一关系.
(1)写出这个反比例函数的表达式(不考虑自变量的取值范围),并补全表格;
(2)在试销8天后,公司决 ( http: / / www.21cnjy.com )定将这种海产品的售价定为150元/kg,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)按(2)中定价继续销售15天后, ( http: / / www.21cnjy.com )公司发现剩余的这些海产品必须在2天内全部售出,此时需要重新确定一个销售价格,使在以后的销售过程中都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
25. 一次函数y=ax+b的图象分别与x轴、y轴交于点M,N,与反比例函数y= (k>0)的图象交于点A(),B().过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图9 图10
(1)若点A,B在反比例函数y=(k>0)的图象的同一分支上,如图9,试证明:①;②AN=BM;
(2)若点A,B分别在反比例函数y= (k>0)的图象的不同分支上,如图10,则AN与BM还相等吗?试证明你的结论.
参考答案及点拨
一、1.D 2.C 3.B
4.A 点拨:当k>0时,y=-kx的图象经过第二、四象限,y=的图象在第一、三象限,无交点;当k<0时,y=-kx的图象经过第一、三象限,y=的图象在第二、四象限,无交点.故交点个数为0.
5.C
6.C 点拨:由于函数图象在第一、三象限,故有m>0,①错误;在每个象限内,y随x的增大而减小,故②错误;将A,B坐标代入,得:h=-m,k=,因为m>0,所以h<k,故③正确;函数图象关于原点对称,故④正确.
7.D 点拨:考查反比例函数比例系数k的几何意义.
二、8.-2 9.< 10.二、四 11.y=(x>0)
12.-1 点拨:此题答案不唯一,k为负数均可.
13.4;-6 14. (-,-2)
15. 24 点拨:由题图设函数关系式为I=,将(9,4)代入,得U=36,故I=,当I=1.5时,R=24.
16. 点拨:把x=2分别代入y=,y=-,得y=1,y=-.∴A(2,1),B(2,-),∴AB=1-(-)=.∵P为y轴上的任意一点,∴点P到直线x=2的距离为2,∴△PAB的面积=AB×2=.
17. 点拨:对于y=,当y=4 029时,x2 015=.对于y=,∵x2 015=,∴y2 015=.
三、18.解:图象如答图1;
观察图象可知,交点坐标为A(1,2),B(-1,-2).
( http: / / www.21cnjy.com )
答图1
19.解:由(x+5)2+ =0,可得 解得
所以点A的坐标为(-5,6).
又因为点A在反比例函数y=的图象上,所以将点A(-5,6)的坐标代入y=,得6=,所以k=-30,故此反比例函数的表达式为y=-.
点拨:解此题的关键在于明白(x+5)2+ =0表示的意义.因为(x+5)2≥0且≥0,要使(x+5)2+ =0,则必须使x+5=0且y-6=0.
20.解:(1)依题意得xy=600,∴y=(0<x<). (2)由y∶x=3∶2,得3x=2y,∴y=,∴x2=600,解得x=20(负值舍去).当x=20时,y=30.∴草坪的长与宽分别是30 m和20 m.
21.解:(1)设y= (k≠0),把x=100,y=30代入y=,得k=3 000,所以y与x之间的函数关系式为y=.
(2)由题意,得(x-80)·y=2 040,即(x-80)·=2 040,解得x=250,经检验x=250是原方程的根,且符合题意.所以每件售价应定为250元.
点拨:(2)中列出的方程为分式方程,得出解后应进行检验.
22.解:(1)把点A的坐标(a,1)代入y1=-x+4,得-a+4=1,解得:a=3,
∴点A的坐标为(3,1).把点A的坐标代入y2=,得k=3,∴函数y2=的表达式为:y2=.
(2)易得b=3,所以由图象可知,当0<x<1或x>3时,y1<y2;当x=1或x=3时,y1= y2 ;当1<x<3时,y1>y2.
23.解:(1)∵B是反比例函数y=图象上的一点,∴把B(2,-4)的坐标代入y=,得-4=,解得m=-8,∴反比例函数的表达式是y=-.把A(-4,n)的坐标代入y=-,得n=-=2,∴点A的坐标为(-4,2).∵点A,B都在一次函数y=kx+b的图象上,∴把A,B两点的坐标分别代入y=kx+b,得解得
∴一次函数的表达式是y=-x-2.
(2)∵点C在x轴上,∴它的纵坐标为0,把y=0代入y=-x-2,得0=-x-2,∴x=-2,∴点C的坐标为(-2,0). ∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=2+4=6.
(3)x=-4或x=2.
(4)-4<x<0或x>2.
24.解:(1)设这个反比例函数的表达式为y=.将x=400,y=30代入y=,解得k=12 000.所以所求反比例函数的表达式为y=.
补全表格如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x(元/ kg) 400 300 250 240 200 150 125 120
销售量y(kg) 30 40 48 50 60 80 96 100
(2)2 104-(30+40+4 ( http: / / www.21cnjy.com )8+50+60+80+96+100)=1 600(kg),即8天试销后,余下的海产品还有1 600 kg.
当x=150时,y=80,1 600÷80=20(天),即余下的这些海产品预计再用20天可以全部售出.
(3)1 600-80×15=400(kg),400÷2=200(kg),即如果正好用2天售完,那么每天需要售出200 kg.当y=200时,x==60,即新确定的价格最高不超过每千克60元才能完成销售任务.
25.(1)证明:①因为AC⊥x轴,AE⊥y轴,所以四边形AEOC为矩形.
因为BF⊥x轴,BD⊥y轴,所以四边形BDOF为矩形.
因为AC⊥x轴,BD⊥y轴,
所以四边形AEDK、四边形DOCK、四边形CFBK均为矩形.
因为OC=x1,AC=y1, x1·y1=k, 所以S矩形AEOC =OC·AC=x1·y1=k.
因为OF=x2,BF=y2,x2·y2=k,所以S矩形BDOF=OF·FB=x2·y2=k,
所以S矩形AEOC=S矩形BDOF.
因为S矩形AEDK=S矩形AEOC- S矩形DOCK,S矩形CFBK=S矩形BDOF-S矩形DOCK,所以S矩形AEDK=S矩形CFBK.
②由①知S矩形AEDK=S矩形CFBK,所以AK·DK=BK·CK.
所以=.又因为∠AKB=∠CKD,所以△ABK∽△CDK,
所以∠ABK=∠CDK,所以AB∥CD.
因为AC∥y轴,所以四边形ACDN是平行四边形,所以AN=CD,同理BM=CD.所以AN=BM.
(2)解:AN与BM仍然相等.
证明:因为S矩形AEDK=S矩形AEOC+S矩形ODKC,
S矩形BKCF=S矩形BDOF+S矩形ODKC,S矩形AEOC=S矩形BDOF=k,
所以S矩形AEDK=S矩形BKCF,所以AK·DK=BK·CK,所以=.
又因为∠K=∠K,所以△CDK∽△ ( http: / / www.21cnjy.com )ABK.所以∠CDK=∠ABK.所以AB∥CD.因为AC∥y轴,所以四边形ANDC是平行四边形,所以AN=CD.同理BM=CD,所以AN=BM.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
