【名师点拨】+2014-2015学年湘教版九年级数学上册过关自测卷:第4章锐角三角函数(含答案)
文档属性
| 名称 | 【名师点拨】+2014-2015学年湘教版九年级数学上册过关自测卷:第4章锐角三角函数(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-29 00:00:00 | ||
图片预览




文档简介
第4章过关自测卷
(90分钟 100分)
一、选择题(每题3分,共30分)
1.图1,P是角α的边OA上一点,点P的坐标为(12,5),则tanα等于( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2 图3
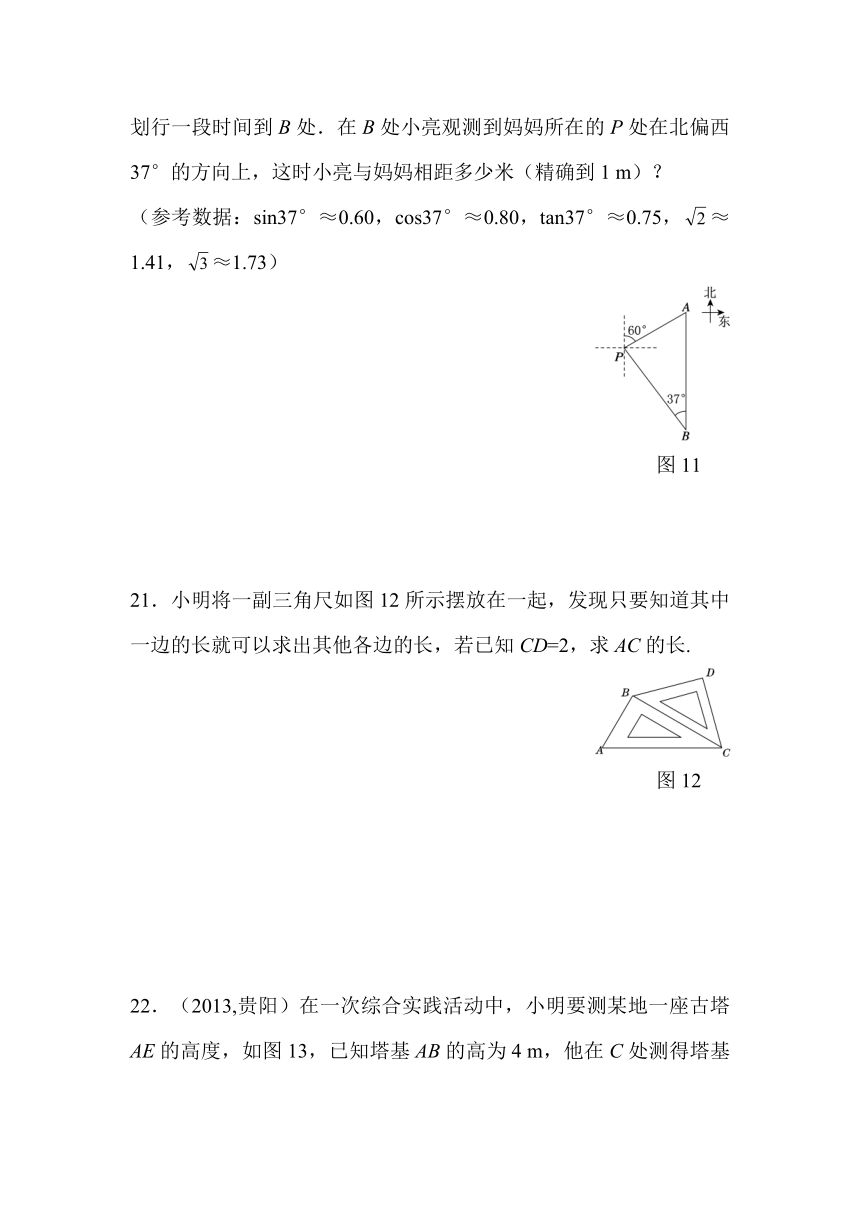
2.在直角三角形ABC中,各边的长度都扩大为原来的2倍,那么锐角A的正弦值、余弦值和正切值( )
A.都扩大为原来的2倍 B.都缩小为原来的
C.都不变 D.无法确定
3.已知在Rt△ABC中,∠C=90°,AC=BC,点D在AC上,∠CBD=
30°,则的值为( )
A. B. C. -1 D.不能确定
4.菱形中较长的对角线的长与较短的对角线的长的比为∶1,则菱形的四个角分别为( )
A.30°、150°、30°、150° B.45°、135°、45°、135°
C.60°、120°、60°、120° D.不能确定
5.如图2,在平地上种植树木时,要求株距 ( http: / / www.21cnjy.com )(相邻两树间的水平距离)为4 m.如果在坡度为0.75的山坡上种树,也要求株距为4 m,那么相邻两树间的坡面距离为( )
A.5 m B.6 m C.7 m D.8 m
6.已知∠A,∠B是Rt△ABC的两个锐角,则方程tanA·x -2x+tanB=0( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.根的情况无法确定
7.如图3,一艘轮船由海平面上A地出发向南 ( http: / / www.21cnjy.com )偏西40°的方向行驶40 n mile到达B地,再由B地向北偏西20°的方向行驶20 n mile到达C地,则A,C两地相距( )
A.30 n mile B.40 n mile C.20 n mile D.10 n mile
8.(2012,四川广安,有改动)如图4,某水库堤坝横断面迎水坡AB的坡度i=1∶,堤坝高BC=50 m,则迎水坡面AB的长度是( )
A.100 m B.100 m C.150 m D.50m
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图4 图5 图6
9.如图5所示,学校的保管室里,有一架5 ( http: / / www.21cnjy.com )m长的梯子OC斜靠在墙上,此时梯子OC与地面所成的角为45°,如果梯子底端O固定不动,顶端C靠到对面墙上的C′点,此时梯子OC′与地面所成的角为60°,则此保管室的宽度AB为( )
A.(+1)m B.(+)m
C.3m D.(+1)m
10.(2013,广州)如 ( http: / / www.21cnjy.com )图6所示,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB等于( )
A.2 B.2 C. D.5
二、填空题(每题3分,共24分)
11.(2012,湖北孝感)计算:cos245°+tan30°·sin60°=________.
12.在△ABC中,∠A,∠B都是锐角,且(cosA-) +|1-tanB|=0,则∠C=__________.
13.若tanα=5,则=__________.
14.如图7,孔明同学背着一桶水,从山 ( http: / / www.21cnjy.com )脚A出发,沿与地面成30°角的山坡向上走,送水到山上因春季受旱缺水的王奶奶家(B处),AB=80 m,则孔明从A到B上升的高度BC是________m.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图7 图8 图9 图10
15.(2014,厦门莲花中学模拟)如图8,△ABC中,∠B=30°,
∠A=15°,若BC边上的高为2,则BC=__________.
16.在△ABC中,∠A,∠B都是锐角,且sinA=,tanB=,AB=10,则△ABC的面积为___________.
17.全市动员修海堤抗台风,某海堤 ( http: / / www.21cnjy.com )的横断面是梯形,如图9所示,迎水坡BC的坡角为30°,背水坡AD的坡度i=1∶1.2,堤顶宽DC为3 m,堤高DF为10 m,则堤底宽AB约为________m.(精确到0.1 m)
18.(2013,荆门)如图10,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE=________.
三、解答题(19题4分,20题6分,24题8分,其余每题7分,共46分)
19.(1)计算:++|1-|-2sin60°·tan60°;
(2)计算:sin 30°+cos 45°+sin60°·tan45°.
20.(2013,昭通)小亮一家在 ( http: / / www.21cnjy.com )一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图11所示).小船从P处出发,沿北偏东60°方向划行200 m到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1 m)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)
( http: / / www.21cnjy.com )
图11
21.小明将一副三角尺如图12所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长,若已知CD=2,求AC的长.
( http: / / www.21cnjy.com )
图12
22.(2013,贵阳)在一次综合实践活动中 ( http: / / www.21cnjy.com ),小明要测某地一座古塔AE的高度,如图13,已知塔基AB的高为4 m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5 m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)
(1)求AC的距离;(结果保留根号)
( http: / / www.21cnjy.com )
图13
(2)求塔高AE.(参考数据:tan50°≈1.2,sin50°≈0.77,
cos50°≈0.64,≈1.73,≈1.41,结果保留整数)
23.如图14,一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10 n mile到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离.(≈1.4, ≈1.7,结果保留整数)
( http: / / www.21cnjy.com )
图14
24.某过街天桥的截面图为梯形,如图15所示,其中天桥斜面CD的坡度i=1∶,CD的长为10 m,天桥另一斜面AB的坡角∠ABG=.
(1)求过街天桥斜面AB的坡度;
(2)求DE的长;
(3)若决定对该过街天桥进行改建,使AB斜面的坡度变缓,将其
45°坡角改为30°,方便过路群众,改建后斜面为AF,试计算此改建需占路面的宽度FB.(结果精确到0.01 m)
图15
25.阅读下列材料,并解决后面的问题.
如图16所示,在锐角三角形ABC中,设∠BAC,∠B,∠C的对边分别是a,b,c.过点A作AD⊥BC于点D,则sinB=,sinC=,即AD=c·sinB,AD=b·sinC.于是c·sinB=b·sinC,即,同理有所以.
即:在一个锐角三角形中,各边和它所对角的正弦的比相等.
( http: / / www.21cnjy.com )
图16
(1)在锐角三角形中,∠A ( http: / / www.21cnjy.com ),∠B,∠C的对边分别是a,b,c,若已知三个元素,a,b,∠A,运用上述结论和有关定理就可以求出其余三个未知元素c,∠B,∠C.请你按照下列步骤填空,完成求解过程.
第一步:由a,b,∠A__________求出∠B;
第二步:由∠A,∠B __________求出∠C;
第三步:由____________________求出c;
(2)一货轮在C处测得灯 ( http: / / www.21cnjy.com )塔A在货轮北偏西30°方向上,随后货轮以28.4 n mile/h的速度按北偏东45°的方向航行,0.5 h后到达B处, 此时又测得灯塔A在货轮的北偏西70°方向上(如图17所示),利用上面的结论求此时货轮到灯塔A的距离AB.(结果精确到0.1 n mile,参考数据:sin40°≈0.643,sin65°≈0.906,sin70°≈0.940,sin75°≈0.966)
( http: / / www.21cnjy.com )
图17
参考答案及点拨
一、1.C 2.C 3.C
4.C 点拨:设较大内角为α,则tan =,所以=60°,所以α=120°.
5.A
6.B 点拨:因为b2-4ac=(-2)2-4·tanA·tanB=4-4×1=0,故方程有两个相等的实数根.
7.C 8.A 9.A
10.B 点拨:过点D作AB的平行线交AC于点E,交BC于点F,如答图1,易知四边形ABFD是平行四边形,∴BF=AD=6,DF=AB=4,∵AB⊥AC,DF∥AB,∴DF⊥AC,又∵CA是∠BCD的平分线,∴CD=CF,∠DCA=∠ACB,又∵AD∥BC,∴∠DAC=∠ACB,∴∠DAC=∠DCA.∴DC=DA=6,∴CF=6,∴BC=BF+CF=12.易求得AC=8,∴tanB= ==2.
( http: / / www.21cnjy.com )
答图1
二、11.1 点拨:cos245°+tan30°·sin60°=+×=+=1.
12.75°
13. 点拨:原式= HYPERLINK "http://www.21cnjy.com" ===.
14.40
15.-2 点拨:设BC边上的高为AD,由题意知,AD=2,∠ACD=∠B+∠BAC=45°,∴tan 45°= ==1,∴CD=2,
∴tan B= ==,解得BC=2-2.
16. 点拨:在该题中,并没有直接指明△ABC是直角三角形,所以需先判断其为直角三角形,然后才能利用解直角三角形的知识解题.
17.32.3
18. 点拨:由题易证△AED∽△ABC,在△ABC中,BC=6,sin A=,可求得AB=10,AC=8.利用相似三角形的性质可求得DE的长.
三、19.解:(1)原式=2+2+1-2××=2+2+1-3=2.
(2)原式=++××1=++=+.
20.解:过P作PC⊥AB于C,如答图2,在Rt△APC中,AP=200 m,∠ACP=,∠PAC=60°.∴PC=200×sin60°=200×=100(m).∵在Rt△PBC中,sin=,∴PB=≈≈288(m).
答:这时小亮与妈妈相距约288 m.
( http: / / www.21cnjy.com )
答图2
21.解:在Rt△BCD中,∠BCD=45°,CD=2,cos∠BCD=,∴BC=
==2.在Rt△ABC中,∠BAC=60°,sin∠BAC=,∴AC= ===.∴AC的长为.
点拨:△ABC和△BCD都是有特殊锐角的直角三角形,所以利用特殊角的三角函数值便可求得AC的长.
22.解:(1)在Rt△ABC中,AB=4 m,∠BCA=30°,由tan∠BCA=,得AC= ===4(m).
∴AC的距离为4 m.
(2)设AE=x m,在Rt△AED中,由tan50°=,得AD=≈(m),
∵CD=AD-AC=5,∴-4≈5,解得x≈14,
∴塔高AE约为14m.
23.解:由题意知:∠BAC=53°-23°=30°,∠C=23°+22°=45°.过点B作BD⊥AC,垂足为D,则CD=BD.∵BC=10 n mile,∴CD=BD=BC·cos45°=10×=5 (n mile),∴AD= HYPERLINK "http://www.21cnjy.com" ≈5×1.4×1.7=11.9(n mile).∴AC=AD+CD≈11.9+≈11.9+7.0=18.9≈19(n mile).
答:此时小船与码头之间的距离约为19 n mile.
24.解:(1)在Rt△AGB中,∠ABG=45°,所以AG=BG.所以AB的坡度为AG∶BG=1∶1.(2)在Rt△DEC中,tanC= ,所以∠C=30°.又因为CD=10 m, 所以DE=CD·sin30°=5 m.(3)由(1)(2)知,AG=BG=DE=5 m,在Rt△AFG中,∠AFG=30°,tan∠AFG=,即.所以FB=-5≈3.66 (m).
答:此改建需占路面的宽度FB约为3.66 m.
25.解:(1);∠A+∠B+∠C=180°;a,∠A,∠C;
(2)根据题意,得∠ABC=180°-45°-70°=65°,∠A=180°-(30°+45°+65°)=40°,BC=0.5×28.4=14.2(n mile).因为,所以AB≈≈21.3(n mile),所以此时货轮到灯塔A的距离AB约为21.3 n mile.
(90分钟 100分)
一、选择题(每题3分,共30分)
1.图1,P是角α的边OA上一点,点P的坐标为(12,5),则tanα等于( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2 图3
2.在直角三角形ABC中,各边的长度都扩大为原来的2倍,那么锐角A的正弦值、余弦值和正切值( )
A.都扩大为原来的2倍 B.都缩小为原来的
C.都不变 D.无法确定
3.已知在Rt△ABC中,∠C=90°,AC=BC,点D在AC上,∠CBD=
30°,则的值为( )
A. B. C. -1 D.不能确定
4.菱形中较长的对角线的长与较短的对角线的长的比为∶1,则菱形的四个角分别为( )
A.30°、150°、30°、150° B.45°、135°、45°、135°
C.60°、120°、60°、120° D.不能确定
5.如图2,在平地上种植树木时,要求株距 ( http: / / www.21cnjy.com )(相邻两树间的水平距离)为4 m.如果在坡度为0.75的山坡上种树,也要求株距为4 m,那么相邻两树间的坡面距离为( )
A.5 m B.6 m C.7 m D.8 m
6.已知∠A,∠B是Rt△ABC的两个锐角,则方程tanA·x -2x+tanB=0( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.根的情况无法确定
7.如图3,一艘轮船由海平面上A地出发向南 ( http: / / www.21cnjy.com )偏西40°的方向行驶40 n mile到达B地,再由B地向北偏西20°的方向行驶20 n mile到达C地,则A,C两地相距( )
A.30 n mile B.40 n mile C.20 n mile D.10 n mile
8.(2012,四川广安,有改动)如图4,某水库堤坝横断面迎水坡AB的坡度i=1∶,堤坝高BC=50 m,则迎水坡面AB的长度是( )
A.100 m B.100 m C.150 m D.50m
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图4 图5 图6
9.如图5所示,学校的保管室里,有一架5 ( http: / / www.21cnjy.com )m长的梯子OC斜靠在墙上,此时梯子OC与地面所成的角为45°,如果梯子底端O固定不动,顶端C靠到对面墙上的C′点,此时梯子OC′与地面所成的角为60°,则此保管室的宽度AB为( )
A.(+1)m B.(+)m
C.3m D.(+1)m
10.(2013,广州)如 ( http: / / www.21cnjy.com )图6所示,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB等于( )
A.2 B.2 C. D.5
二、填空题(每题3分,共24分)
11.(2012,湖北孝感)计算:cos245°+tan30°·sin60°=________.
12.在△ABC中,∠A,∠B都是锐角,且(cosA-) +|1-tanB|=0,则∠C=__________.
13.若tanα=5,则=__________.
14.如图7,孔明同学背着一桶水,从山 ( http: / / www.21cnjy.com )脚A出发,沿与地面成30°角的山坡向上走,送水到山上因春季受旱缺水的王奶奶家(B处),AB=80 m,则孔明从A到B上升的高度BC是________m.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图7 图8 图9 图10
15.(2014,厦门莲花中学模拟)如图8,△ABC中,∠B=30°,
∠A=15°,若BC边上的高为2,则BC=__________.
16.在△ABC中,∠A,∠B都是锐角,且sinA=,tanB=,AB=10,则△ABC的面积为___________.
17.全市动员修海堤抗台风,某海堤 ( http: / / www.21cnjy.com )的横断面是梯形,如图9所示,迎水坡BC的坡角为30°,背水坡AD的坡度i=1∶1.2,堤顶宽DC为3 m,堤高DF为10 m,则堤底宽AB约为________m.(精确到0.1 m)
18.(2013,荆门)如图10,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE=________.
三、解答题(19题4分,20题6分,24题8分,其余每题7分,共46分)
19.(1)计算:++|1-|-2sin60°·tan60°;
(2)计算:sin 30°+cos 45°+sin60°·tan45°.
20.(2013,昭通)小亮一家在 ( http: / / www.21cnjy.com )一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图11所示).小船从P处出发,沿北偏东60°方向划行200 m到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1 m)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)
( http: / / www.21cnjy.com )
图11
21.小明将一副三角尺如图12所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长,若已知CD=2,求AC的长.
( http: / / www.21cnjy.com )
图12
22.(2013,贵阳)在一次综合实践活动中 ( http: / / www.21cnjy.com ),小明要测某地一座古塔AE的高度,如图13,已知塔基AB的高为4 m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5 m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)
(1)求AC的距离;(结果保留根号)
( http: / / www.21cnjy.com )
图13
(2)求塔高AE.(参考数据:tan50°≈1.2,sin50°≈0.77,
cos50°≈0.64,≈1.73,≈1.41,结果保留整数)
23.如图14,一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10 n mile到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离.(≈1.4, ≈1.7,结果保留整数)
( http: / / www.21cnjy.com )
图14
24.某过街天桥的截面图为梯形,如图15所示,其中天桥斜面CD的坡度i=1∶,CD的长为10 m,天桥另一斜面AB的坡角∠ABG=.
(1)求过街天桥斜面AB的坡度;
(2)求DE的长;
(3)若决定对该过街天桥进行改建,使AB斜面的坡度变缓,将其
45°坡角改为30°,方便过路群众,改建后斜面为AF,试计算此改建需占路面的宽度FB.(结果精确到0.01 m)
图15
25.阅读下列材料,并解决后面的问题.
如图16所示,在锐角三角形ABC中,设∠BAC,∠B,∠C的对边分别是a,b,c.过点A作AD⊥BC于点D,则sinB=,sinC=,即AD=c·sinB,AD=b·sinC.于是c·sinB=b·sinC,即,同理有所以.
即:在一个锐角三角形中,各边和它所对角的正弦的比相等.
( http: / / www.21cnjy.com )
图16
(1)在锐角三角形中,∠A ( http: / / www.21cnjy.com ),∠B,∠C的对边分别是a,b,c,若已知三个元素,a,b,∠A,运用上述结论和有关定理就可以求出其余三个未知元素c,∠B,∠C.请你按照下列步骤填空,完成求解过程.
第一步:由a,b,∠A__________求出∠B;
第二步:由∠A,∠B __________求出∠C;
第三步:由____________________求出c;
(2)一货轮在C处测得灯 ( http: / / www.21cnjy.com )塔A在货轮北偏西30°方向上,随后货轮以28.4 n mile/h的速度按北偏东45°的方向航行,0.5 h后到达B处, 此时又测得灯塔A在货轮的北偏西70°方向上(如图17所示),利用上面的结论求此时货轮到灯塔A的距离AB.(结果精确到0.1 n mile,参考数据:sin40°≈0.643,sin65°≈0.906,sin70°≈0.940,sin75°≈0.966)
( http: / / www.21cnjy.com )
图17
参考答案及点拨
一、1.C 2.C 3.C
4.C 点拨:设较大内角为α,则tan =,所以=60°,所以α=120°.
5.A
6.B 点拨:因为b2-4ac=(-2)2-4·tanA·tanB=4-4×1=0,故方程有两个相等的实数根.
7.C 8.A 9.A
10.B 点拨:过点D作AB的平行线交AC于点E,交BC于点F,如答图1,易知四边形ABFD是平行四边形,∴BF=AD=6,DF=AB=4,∵AB⊥AC,DF∥AB,∴DF⊥AC,又∵CA是∠BCD的平分线,∴CD=CF,∠DCA=∠ACB,又∵AD∥BC,∴∠DAC=∠ACB,∴∠DAC=∠DCA.∴DC=DA=6,∴CF=6,∴BC=BF+CF=12.易求得AC=8,∴tanB= ==2.
( http: / / www.21cnjy.com )
答图1
二、11.1 点拨:cos245°+tan30°·sin60°=+×=+=1.
12.75°
13. 点拨:原式= HYPERLINK "http://www.21cnjy.com" ===.
14.40
15.-2 点拨:设BC边上的高为AD,由题意知,AD=2,∠ACD=∠B+∠BAC=45°,∴tan 45°= ==1,∴CD=2,
∴tan B= ==,解得BC=2-2.
16. 点拨:在该题中,并没有直接指明△ABC是直角三角形,所以需先判断其为直角三角形,然后才能利用解直角三角形的知识解题.
17.32.3
18. 点拨:由题易证△AED∽△ABC,在△ABC中,BC=6,sin A=,可求得AB=10,AC=8.利用相似三角形的性质可求得DE的长.
三、19.解:(1)原式=2+2+1-2××=2+2+1-3=2.
(2)原式=++××1=++=+.
20.解:过P作PC⊥AB于C,如答图2,在Rt△APC中,AP=200 m,∠ACP=,∠PAC=60°.∴PC=200×sin60°=200×=100(m).∵在Rt△PBC中,sin=,∴PB=≈≈288(m).
答:这时小亮与妈妈相距约288 m.
( http: / / www.21cnjy.com )
答图2
21.解:在Rt△BCD中,∠BCD=45°,CD=2,cos∠BCD=,∴BC=
==2.在Rt△ABC中,∠BAC=60°,sin∠BAC=,∴AC= ===.∴AC的长为.
点拨:△ABC和△BCD都是有特殊锐角的直角三角形,所以利用特殊角的三角函数值便可求得AC的长.
22.解:(1)在Rt△ABC中,AB=4 m,∠BCA=30°,由tan∠BCA=,得AC= ===4(m).
∴AC的距离为4 m.
(2)设AE=x m,在Rt△AED中,由tan50°=,得AD=≈(m),
∵CD=AD-AC=5,∴-4≈5,解得x≈14,
∴塔高AE约为14m.
23.解:由题意知:∠BAC=53°-23°=30°,∠C=23°+22°=45°.过点B作BD⊥AC,垂足为D,则CD=BD.∵BC=10 n mile,∴CD=BD=BC·cos45°=10×=5 (n mile),∴AD= HYPERLINK "http://www.21cnjy.com" ≈5×1.4×1.7=11.9(n mile).∴AC=AD+CD≈11.9+≈11.9+7.0=18.9≈19(n mile).
答:此时小船与码头之间的距离约为19 n mile.
24.解:(1)在Rt△AGB中,∠ABG=45°,所以AG=BG.所以AB的坡度为AG∶BG=1∶1.(2)在Rt△DEC中,tanC= ,所以∠C=30°.又因为CD=10 m, 所以DE=CD·sin30°=5 m.(3)由(1)(2)知,AG=BG=DE=5 m,在Rt△AFG中,∠AFG=30°,tan∠AFG=,即.所以FB=-5≈3.66 (m).
答:此改建需占路面的宽度FB约为3.66 m.
25.解:(1);∠A+∠B+∠C=180°;a,∠A,∠C;
(2)根据题意,得∠ABC=180°-45°-70°=65°,∠A=180°-(30°+45°+65°)=40°,BC=0.5×28.4=14.2(n mile).因为,所以AB≈≈21.3(n mile),所以此时货轮到灯塔A的距离AB约为21.3 n mile.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
