江苏省淮安市2013-2014学年度高一年级学业质量调查测试
文档属性
| 名称 | 江苏省淮安市2013-2014学年度高一年级学业质量调查测试 | 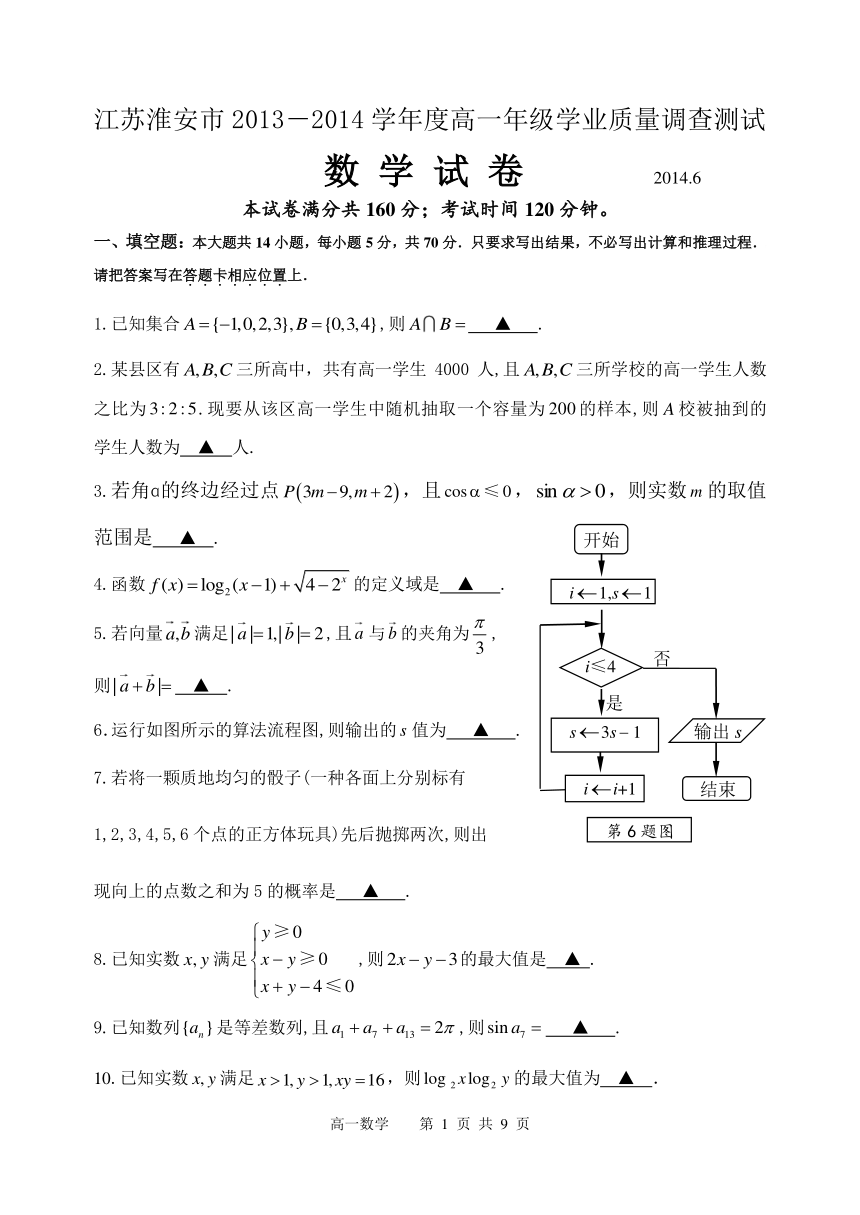 | |
| 格式 | zip | ||
| 文件大小 | 256.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-29 22:09:50 | ||
图片预览




文档简介
江苏淮安市2013-2014学年度高一年级学业质量调查测试
数 学 试 卷 2014.6
本试卷满分共160分;考试时间120分钟。
一、填空题:本大题共14小题,每小题5分,共70分.只要求写出结果,不必写出计算和推理过程.请把答案写在答题卡相应位置上.
1.已知集合,则 ▲ .
2.某县区有三所高中,共有高一学生4000人,且三所学校的高一学生人数之比为.现要从该区高一学生中随机抽取一个容量为的样本,则校被抽到的学生人数为 ▲ 人.
3.若角ɑ的终边经过点,且,,则实数的取值范围是 ▲ .
4.函数的定义域是 ▲ .
5.若向量满足,且与的夹角为,
则 ▲ .
6.运行如图所示的算法流程图,则输出的值为 ▲ .
7.若将一颗质地均匀的骰子(一种各面上分别标有
1,2,3,4,5,6个点的正方体玩具)先后抛掷两次,则出
现向上的点数之和为5的概率是 ▲ .
8.已知实数满足,则的最大值是 ▲ .
9.已知数列是等差数列,且,则 ▲ .
10.已知实数满足,则的最大值为 ▲ .
11.已知,,则= ▲ .
12.已知为等比数列,是它的前项和.若,且与的等差中项为,则 ▲ .
13.已知为的边上一点,若,则的最大值为 ▲ .
14.正项数列满足,又数列是以为公比的等比数列,则使得不等式成立的最大整数为 ▲ .
二.解答题:本大题共6小题,共计90分.解答时应写出文字说明,证明过程或演算步骤.请把答案写在答题卡相应位置上.
15.(本小题满分14分)
已知向量.
(1) 若∥,求的值;
(2) 若,且,求的值.
16.(本小题满分14分)
已知的周长为,且.
(1) 求边的长;
(2) 若的面积为,求角的值.
17.(本小题满分14分)
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,
制成如图所示的茎叶图.
(1)根据样本数据,计算甲、乙两个车间产品重量的
均值与方差,并说明哪个车间的产品的重量相对稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2克的概率.
18.(本小题满分16分)
在某文艺会场中央有一块边长为米(为常数)的正方形地面全彩LED显示屏如图所示,点分别为边上异于点的动点.现在顶点处有视角的摄像机,正录制移动区域内表演的某个文艺节目.设米,米.
(1) 试将表示为的函数;
(2) 求面积的最大值.
19.(本小题满分16分)
已知函数.
(1) 若关于的不等式的解集为,求实数的值;
(2) 设,若不等式对任意实数都成立,求实数的取值范围;
(3) 设,解关于的不等式组.
20.(本小题满分16分)
已知递增数列的前项和为,且满足,.设,且数列的前项和为.
(1) 求证:数列为等差数列;
(2) 试求所有的正整数,使得为整数;
(3) 若对任意的,不等式恒成立,求实数的取值范围.
江苏省淮安市2013-2014学年度高一年级学业质量调查测试
数学参考答案与评分标准
一、填空题:
1.; 2.; 3.; 4. ; 5. ; 6. ; 7. ;
8.; 9. ; 10.4; 11.1; 12.31; 13.; 14.;
二.解答题
15. (1)因为//,所以,……………………………………………2分
所以,即,………………………………4分
解得或(舍去),所以. ……………………………………7分
(2)因为,所以,即,
所以,即, ………………………………………………………9分
因为,所以,所以,
, ………………………………………………………………12分
所以. …………14分
16. (1)设所对的边分别为,由,
得, ……………………………………………………2分
又因为,所以,即, ……………4分
又,所以,,即.……………………………6分
(2)由已知得,因为,所以, ……………………8分
由(1)知,所以
, …………………………………………………………………………12分
因为,所以. ……………………………………………………………14分
17.(1)设甲、乙两个车间产品重量的均值分别为 ,方差分别为 、, 则,……………………………1分 ,………………………………2分
, ………………………4分
, …………………6分
由于,所以甲车间的产品的重量相对稳定;………………………………7分
(2)从乙车间6件样品中随机抽取两件,结果共有15个:
.…………………………9分
设所抽取两件样品重量之差不超过2克的事件为A,则事件A共有4个结果:
.………………………………………11分
所以抽取两件样品重量之差不超过2克的概率为.………………………14分
18.(1)由题意得,
因为,所以,…………………………………………2分
所以,即,………………5分
所以,其中. ………………………………………………………7分
(2)由,知的面积
,…………………………………………9分
设,则,其中,所以
,…………14分
当且仅当,即时取等号, …………………………………………15分
故面积的最大值为.………………………………………………16分
19. (1)因为不等式的解集为,
所以由题意得为函数的两个根,
所以,解得.……………………………………4分
(2)当时,恒成立,即恒成立.
因为 ,所以, ………………………………6分
解之得,所以实数的取值范围为.……………………………………8分
(3)当时,,的图象的对称轴为.
(ⅰ)当,即时,由,得,…………………………………10分
(ⅱ)当,即或时
①当时,由,得,所以,
②当时,由,得,所以或,………………12分
(ⅲ)当,即或时,方程的两个根为,
,
①当时,由知,所以的解为或,
②当时,由知,所以的解为,…………………14分
综上所述,
当时,不等式组的解集为,
当时,不等式组的解集为.…………………………………………………16分
20.(1)由,得,………………………2分
所以,即,即,
所以或,
即或,……………………………………………4分
若,则有,又,所以,则,这与数列递增矛盾,所以,故数列为等差数列.……………………………6分
(2) 由(1)知,所以
,………………………………………8分
因为,所以,又且为奇数,所以或,故的值为或.……………………………………………………………10分
(3) 由(1)知,则,
所以
,……………………………………………………………………12分
从而对任意恒成立等价于,
当为奇数时,恒成立,
记,则,当时取等号,所以,
当为偶数时,恒成立.
记,因为递增,所以,
所以.综上,实数的取值范围为.………………………………………16分
第17题图
7 10 8 9
4 3 1 1 11 0 2 5
2 12 4
甲 乙
第18题图
第6题图
i≤4
输出s
否
是
结束
开始
ii+1
s3s1
i1,s1
高一数学 第 4 页 共 9 页
数 学 试 卷 2014.6
本试卷满分共160分;考试时间120分钟。
一、填空题:本大题共14小题,每小题5分,共70分.只要求写出结果,不必写出计算和推理过程.请把答案写在答题卡相应位置上.
1.已知集合,则 ▲ .
2.某县区有三所高中,共有高一学生4000人,且三所学校的高一学生人数之比为.现要从该区高一学生中随机抽取一个容量为的样本,则校被抽到的学生人数为 ▲ 人.
3.若角ɑ的终边经过点,且,,则实数的取值范围是 ▲ .
4.函数的定义域是 ▲ .
5.若向量满足,且与的夹角为,
则 ▲ .
6.运行如图所示的算法流程图,则输出的值为 ▲ .
7.若将一颗质地均匀的骰子(一种各面上分别标有
1,2,3,4,5,6个点的正方体玩具)先后抛掷两次,则出
现向上的点数之和为5的概率是 ▲ .
8.已知实数满足,则的最大值是 ▲ .
9.已知数列是等差数列,且,则 ▲ .
10.已知实数满足,则的最大值为 ▲ .
11.已知,,则= ▲ .
12.已知为等比数列,是它的前项和.若,且与的等差中项为,则 ▲ .
13.已知为的边上一点,若,则的最大值为 ▲ .
14.正项数列满足,又数列是以为公比的等比数列,则使得不等式成立的最大整数为 ▲ .
二.解答题:本大题共6小题,共计90分.解答时应写出文字说明,证明过程或演算步骤.请把答案写在答题卡相应位置上.
15.(本小题满分14分)
已知向量.
(1) 若∥,求的值;
(2) 若,且,求的值.
16.(本小题满分14分)
已知的周长为,且.
(1) 求边的长;
(2) 若的面积为,求角的值.
17.(本小题满分14分)
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,
制成如图所示的茎叶图.
(1)根据样本数据,计算甲、乙两个车间产品重量的
均值与方差,并说明哪个车间的产品的重量相对稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2克的概率.
18.(本小题满分16分)
在某文艺会场中央有一块边长为米(为常数)的正方形地面全彩LED显示屏如图所示,点分别为边上异于点的动点.现在顶点处有视角的摄像机,正录制移动区域内表演的某个文艺节目.设米,米.
(1) 试将表示为的函数;
(2) 求面积的最大值.
19.(本小题满分16分)
已知函数.
(1) 若关于的不等式的解集为,求实数的值;
(2) 设,若不等式对任意实数都成立,求实数的取值范围;
(3) 设,解关于的不等式组.
20.(本小题满分16分)
已知递增数列的前项和为,且满足,.设,且数列的前项和为.
(1) 求证:数列为等差数列;
(2) 试求所有的正整数,使得为整数;
(3) 若对任意的,不等式恒成立,求实数的取值范围.
江苏省淮安市2013-2014学年度高一年级学业质量调查测试
数学参考答案与评分标准
一、填空题:
1.; 2.; 3.; 4. ; 5. ; 6. ; 7. ;
8.; 9. ; 10.4; 11.1; 12.31; 13.; 14.;
二.解答题
15. (1)因为//,所以,……………………………………………2分
所以,即,………………………………4分
解得或(舍去),所以. ……………………………………7分
(2)因为,所以,即,
所以,即, ………………………………………………………9分
因为,所以,所以,
, ………………………………………………………………12分
所以. …………14分
16. (1)设所对的边分别为,由,
得, ……………………………………………………2分
又因为,所以,即, ……………4分
又,所以,,即.……………………………6分
(2)由已知得,因为,所以, ……………………8分
由(1)知,所以
, …………………………………………………………………………12分
因为,所以. ……………………………………………………………14分
17.(1)设甲、乙两个车间产品重量的均值分别为 ,方差分别为 、, 则,……………………………1分 ,………………………………2分
, ………………………4分
, …………………6分
由于,所以甲车间的产品的重量相对稳定;………………………………7分
(2)从乙车间6件样品中随机抽取两件,结果共有15个:
.…………………………9分
设所抽取两件样品重量之差不超过2克的事件为A,则事件A共有4个结果:
.………………………………………11分
所以抽取两件样品重量之差不超过2克的概率为.………………………14分
18.(1)由题意得,
因为,所以,…………………………………………2分
所以,即,………………5分
所以,其中. ………………………………………………………7分
(2)由,知的面积
,…………………………………………9分
设,则,其中,所以
,…………14分
当且仅当,即时取等号, …………………………………………15分
故面积的最大值为.………………………………………………16分
19. (1)因为不等式的解集为,
所以由题意得为函数的两个根,
所以,解得.……………………………………4分
(2)当时,恒成立,即恒成立.
因为 ,所以, ………………………………6分
解之得,所以实数的取值范围为.……………………………………8分
(3)当时,,的图象的对称轴为.
(ⅰ)当,即时,由,得,…………………………………10分
(ⅱ)当,即或时
①当时,由,得,所以,
②当时,由,得,所以或,………………12分
(ⅲ)当,即或时,方程的两个根为,
,
①当时,由知,所以的解为或,
②当时,由知,所以的解为,…………………14分
综上所述,
当时,不等式组的解集为,
当时,不等式组的解集为.…………………………………………………16分
20.(1)由,得,………………………2分
所以,即,即,
所以或,
即或,……………………………………………4分
若,则有,又,所以,则,这与数列递增矛盾,所以,故数列为等差数列.……………………………6分
(2) 由(1)知,所以
,………………………………………8分
因为,所以,又且为奇数,所以或,故的值为或.……………………………………………………………10分
(3) 由(1)知,则,
所以
,……………………………………………………………………12分
从而对任意恒成立等价于,
当为奇数时,恒成立,
记,则,当时取等号,所以,
当为偶数时,恒成立.
记,因为递增,所以,
所以.综上,实数的取值范围为.………………………………………16分
第17题图
7 10 8 9
4 3 1 1 11 0 2 5
2 12 4
甲 乙
第18题图
第6题图
i≤4
输出s
否
是
结束
开始
ii+1
s3s1
i1,s1
高一数学 第 4 页 共 9 页
同课章节目录
