比和比例总复习课件六年级下册数学人教版(共21张PPT)
文档属性
| 名称 | 比和比例总复习课件六年级下册数学人教版(共21张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 05:47:59 | ||
图片预览


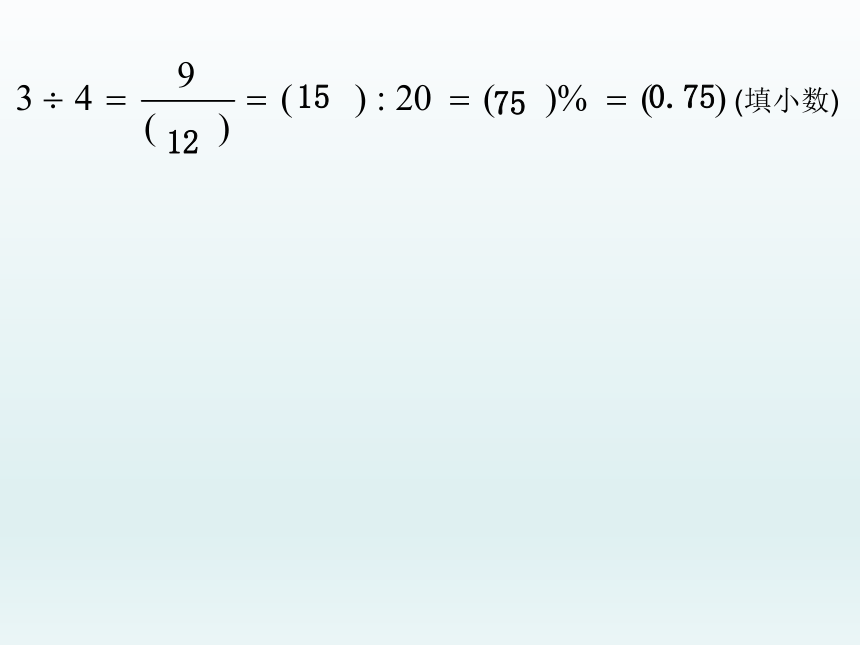




文档简介
(共21张PPT)
知识归纳
巩固练习
一、数与代数——5.比和比例
意义 各部分名称 (举例说明) 基本性质 区别
比 表示两个数相除 9 : 6 = 1 .5 前 比 后 比 项 号 项 值 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 表示两个数相除。
由两个数组成,是一个式子。
比例 表示两个比相等的式子 9 :6 = 3 :2 在比例里,两个外项的积等于两内项的积。 表示两个比相等的式子。
由四个数组成,是一个等式。
比和比例的区别
内项
外项
求比值和化简比的区别:
求比值:比的前项除以比的后项。
化简比:比的前项和后项同时乘或除 以相同的数(0除外)。
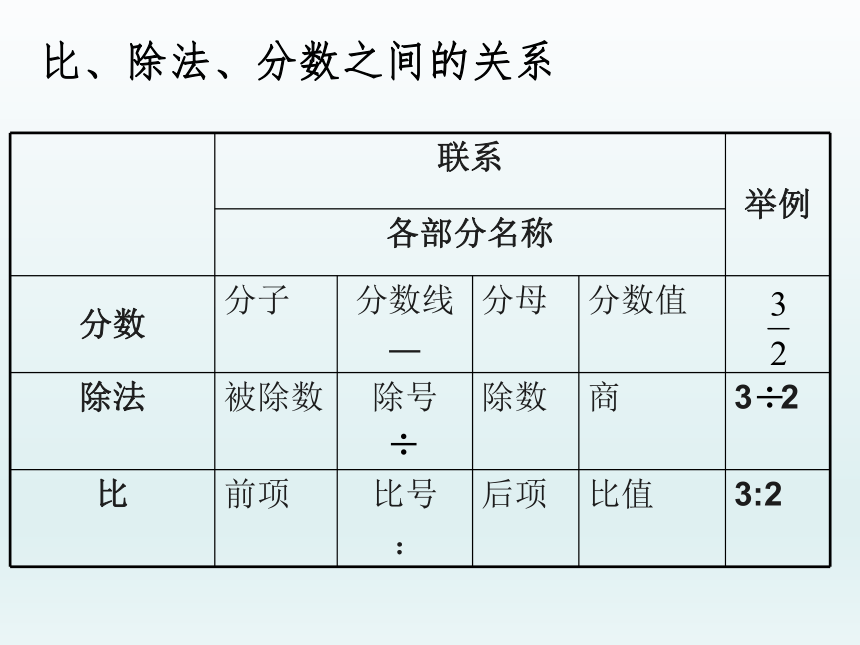
(填小数)
12
15
75
0.75
联系 举例
各部分名称 分数 分子 分数线 ― 分母 分数值
除法 被除数 除号 除数 商 3 2
比 前项 比号 : 后项 比值 3:2
比、除法、分数之间的关系
它们之间的联系可以用字母表示为:
4.正比例和反比例的意义
正比例意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例关系式:y : x = k(一定)
反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
反比例关系式:xy = k (一定)
1.《小学生作文》的单价一定,订阅的费用与订阅 的数量。 ( )
2. 圆柱体积一定,圆柱的底面积与高。 ( )
3. 一个人的身高与他的年龄。 ( )4. 小麦每公顷产量一定,小麦的总产量与公顷数。
( )
5. 书的总页数一定,未读的页数与已读的页数( )
6. 正方体的棱长和棱长总和。 ( )
请你判断下面各题中的两种量是否成比例。如果成比例,成什么比例?
正比例
正比例
正比例
反比例
不成比例
不成比例
知 识 归 纳
正比例、反比例的判断方法
简言之,即“一找二看三判断”:
(1)找变量:分析数量关系,确定两种量是否是相关联 的量。
(2)看定量:分析这两种相关联的量,它们之间的关系是商一定,还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成比例。
判断下面哪个是正比例图像?那个是反比例图像?
正比例
反比例
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
比例尺
1、比例尺的意义:
数值比例尺
线段比例尺
1:5000000
0 50km
按形式分:
缩小比例尺
放大比例尺
按用途分:
1:5000000
50:1
2、比例尺的分类:
(1)比例尺是一个比,不能带有计量单位;
(2)求比例尺时,前、后项的单位长度一 定要统一成同级单位;
(3)比例尺的前项或后项,一般应化简成“1”。
强调
练一练:
某建筑工地挖一个长方形的地基,把它画在比例尺是1 :2000的平面图上,长是6厘米,宽是4厘米,这块地基的面积是多少平方米?
㎡
答:这块地基的面积是9600平方米.
图形的放大与缩小的特点是:
形状相同,大小不同。
图形的放大与缩小
1、甲地到乙地的公路长392千米。一辆汽车3小时行了168千米。照这样计算,行完全程共需要几小时
解:设行完全程共需要x小时
答:行完全程共需要7小时.
(1)设未知数为x;
(2)判断题中的两种量成正比例还是成反比例关系;
(3)列比例式;
(4)解 答。
用比例解决问题的步骤:
一、填空。
1、如果a=—,那么当( )一定时,( )和( )成正比例。当( )一定时,( )和( )成反比例。
2、小圆的半径是2厘米,大圆的半径是3厘米,大圆和小圆的周长比是( )。
3、甲、乙两数的比是5 :3,乙数是60,甲数是( )。
b
c
b
c
a
3:2
100
a
b
c
解:设甲乙两地相距X千米。
答:甲乙两地相距150km。
用比例解决问题
解:设返回时用了X小时。
答:返回时用了2.5小时。
随随便便浪费的时间,
再也不能赢回来。
知识归纳
巩固练习
一、数与代数——5.比和比例
意义 各部分名称 (举例说明) 基本性质 区别
比 表示两个数相除 9 : 6 = 1 .5 前 比 后 比 项 号 项 值 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 表示两个数相除。
由两个数组成,是一个式子。
比例 表示两个比相等的式子 9 :6 = 3 :2 在比例里,两个外项的积等于两内项的积。 表示两个比相等的式子。
由四个数组成,是一个等式。
比和比例的区别
内项
外项
求比值和化简比的区别:
求比值:比的前项除以比的后项。
化简比:比的前项和后项同时乘或除 以相同的数(0除外)。
(填小数)
12
15
75
0.75
联系 举例
各部分名称 分数 分子 分数线 ― 分母 分数值
除法 被除数 除号 除数 商 3 2
比 前项 比号 : 后项 比值 3:2
比、除法、分数之间的关系
它们之间的联系可以用字母表示为:
4.正比例和反比例的意义
正比例意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例关系式:y : x = k(一定)
反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
反比例关系式:xy = k (一定)
1.《小学生作文》的单价一定,订阅的费用与订阅 的数量。 ( )
2. 圆柱体积一定,圆柱的底面积与高。 ( )
3. 一个人的身高与他的年龄。 ( )4. 小麦每公顷产量一定,小麦的总产量与公顷数。
( )
5. 书的总页数一定,未读的页数与已读的页数( )
6. 正方体的棱长和棱长总和。 ( )
请你判断下面各题中的两种量是否成比例。如果成比例,成什么比例?
正比例
正比例
正比例
反比例
不成比例
不成比例
知 识 归 纳
正比例、反比例的判断方法
简言之,即“一找二看三判断”:
(1)找变量:分析数量关系,确定两种量是否是相关联 的量。
(2)看定量:分析这两种相关联的量,它们之间的关系是商一定,还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成比例。
判断下面哪个是正比例图像?那个是反比例图像?
正比例
反比例
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
比例尺
1、比例尺的意义:
数值比例尺
线段比例尺
1:5000000
0 50km
按形式分:
缩小比例尺
放大比例尺
按用途分:
1:5000000
50:1
2、比例尺的分类:
(1)比例尺是一个比,不能带有计量单位;
(2)求比例尺时,前、后项的单位长度一 定要统一成同级单位;
(3)比例尺的前项或后项,一般应化简成“1”。
强调
练一练:
某建筑工地挖一个长方形的地基,把它画在比例尺是1 :2000的平面图上,长是6厘米,宽是4厘米,这块地基的面积是多少平方米?
㎡
答:这块地基的面积是9600平方米.
图形的放大与缩小的特点是:
形状相同,大小不同。
图形的放大与缩小
1、甲地到乙地的公路长392千米。一辆汽车3小时行了168千米。照这样计算,行完全程共需要几小时
解:设行完全程共需要x小时
答:行完全程共需要7小时.
(1)设未知数为x;
(2)判断题中的两种量成正比例还是成反比例关系;
(3)列比例式;
(4)解 答。
用比例解决问题的步骤:
一、填空。
1、如果a=—,那么当( )一定时,( )和( )成正比例。当( )一定时,( )和( )成反比例。
2、小圆的半径是2厘米,大圆的半径是3厘米,大圆和小圆的周长比是( )。
3、甲、乙两数的比是5 :3,乙数是60,甲数是( )。
b
c
b
c
a
3:2
100
a
b
c
解:设甲乙两地相距X千米。
答:甲乙两地相距150km。
用比例解决问题
解:设返回时用了X小时。
答:返回时用了2.5小时。
随随便便浪费的时间,
再也不能赢回来。
