北师大版数学七年级下册 4.1《认识三角形》专项练习(含答案)
文档属性
| 名称 | 北师大版数学七年级下册 4.1《认识三角形》专项练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 156.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 00:00:00 | ||
图片预览


文档简介
北师大版数学七年级下册
《认识三角形》专项练习
一 、选择题
1.下列长度的三条线段,能构成三角形的是( )
A.1,2,6 B.1,2,3 C.2,3,4 D.2,2,4
2.一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是( )
A.14 B.15 C.16 D.17
3.在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )
A.1cm<AB<4cm B.5cm<AB<10cm C.4cm<AB<8cm D.4cm<AB<10cm
4.若三角形三个内角的比为1:2:3,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.钝角三角形
5.如图,一个60o角的三角形纸片,剪去这个600角后,得到一个四边形,则么的度数为( )
A.120O B.180O C.240O D.3000
6.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A. B.
C. D.
7.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
8.若a、b、c是△ABC的三边的长,则化简|a-b-c|-|b-c-a|+|a+b-c|=( )
A.a+b+c B.﹣a+3b﹣c C.a+b﹣c D.2b﹣2c
9.如图,在Rt△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A.120° B.108° C.72° D.36°
10.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠DOF=142°,则∠C的度数为( )
A.38° B.39° C.42° D.48°
11.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E.那么∠B等于( )
A.80° B.60° C.40° D.30°
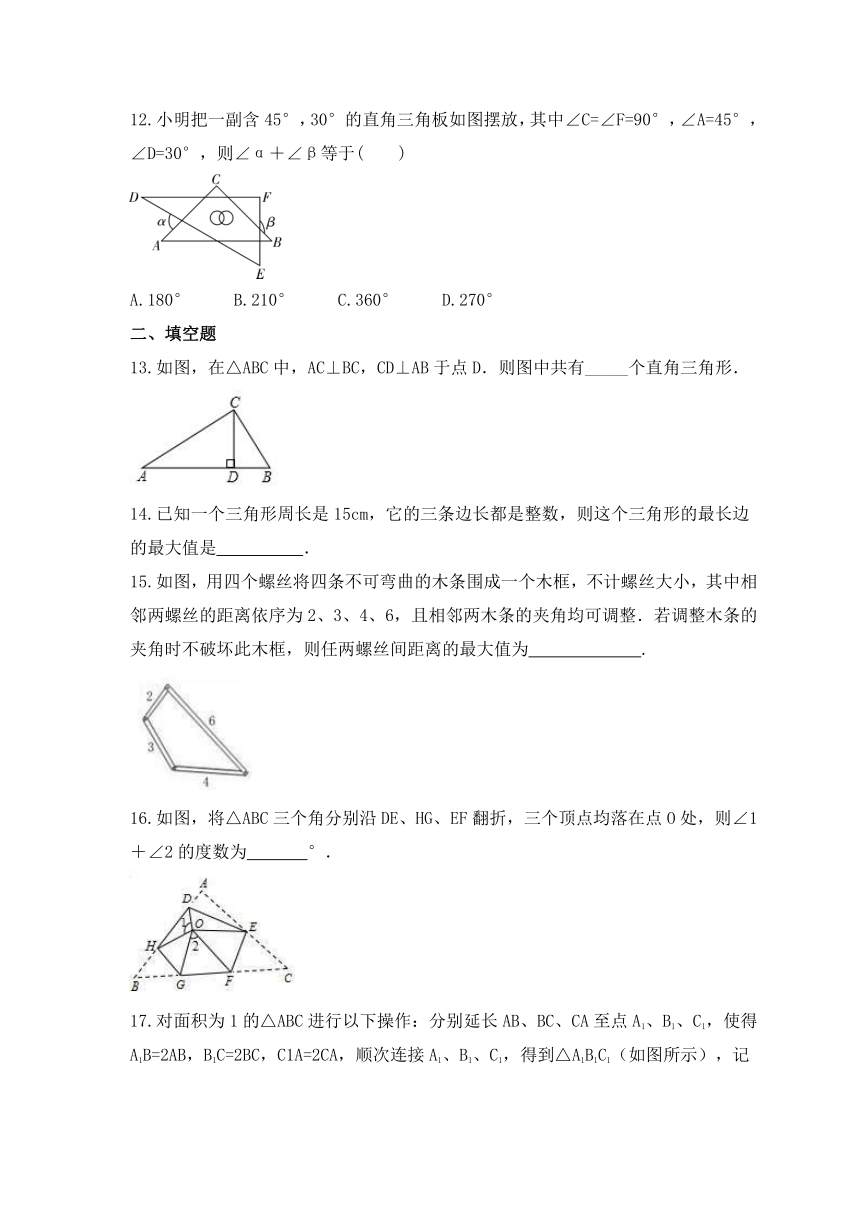
12.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
二 、填空题
13.如图,在△ABC中,AC⊥BC,CD⊥AB于点D.则图中共有_____个直角三角形.
14.已知一个三角形周长是15cm,它的三条边长都是整数,则这个三角形的最长边的最大值是 .
15.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝间距离的最大值为 .
16.如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为 °.
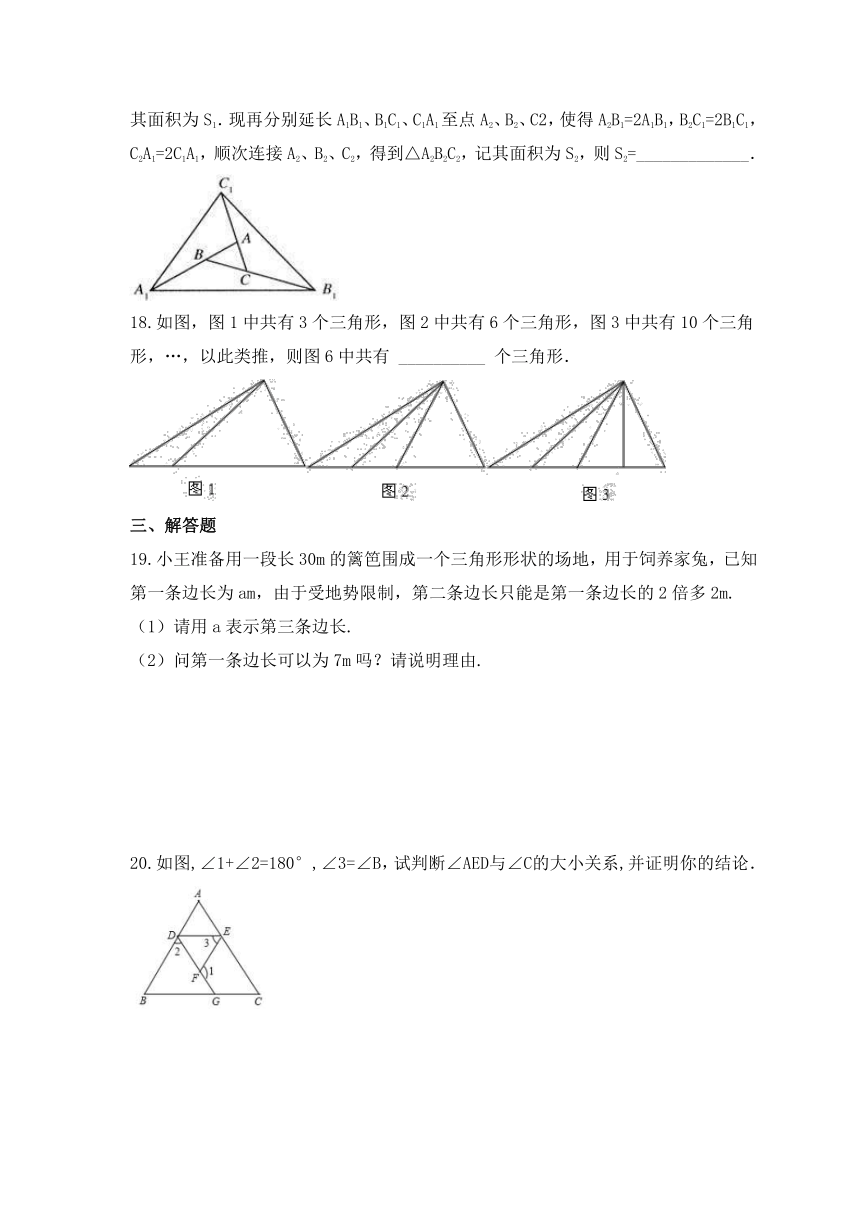
17.对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1(如图所示),记其面积为S1.现再分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2,则S2=_____________.
18.如图,图1中共有3个三角形,图2中共有6个三角形,图3中共有10个三角形,…,以此类推,则图6中共有 __________ 个三角形.
三 、解答题
19.小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.
(1)请用a表示第三条边长.
(2)问第一条边长可以为7m吗?请说明理由.
20.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
21.如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,
求∠BCD和∠ECD的度数.
22.已知a,b,c是三角形的三边长.
(1)化简:|b+c-a|+|b-c-a|-|c-a-b|-|a-b+c|;
(2)在(1)的条件下,若a,b,c满足a+b=11,b+c=9,a+c=10,求这个式子的值.
23.将一副三角板叠放在一起:
(1)如图1,在此种图案的情形下,如果∠ɑ=3∠β,求∠CAE的度数;
(2)如图2,在此种图案的情形下,∠ACE=2∠BCD是否成立?若成立,请求出∠ACD的度数;若不成立,请说明理由.
24.如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置,通过计算我们知道:2∠A=∠l+∠2.请你继续探索:
(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,如图②,此时∠A与∠1、∠2之间存在什么样的关系
(2)如果把四边形ABCD沿时折叠,使点A、D落在四边形BCFE的内部A′、D′的位置,如图③,你能求出∠A、∠D、∠l与∠2之间的关系吗 (直接写出关系式即可)
答案
1.C
2.B
3.B
4.B
5.C.
6.A.
7.D
8.B
9.B
10.A
11.C
12.B
13.答案为:3
14.答案为:5或6或7;
15.答案为:7
16.答案为:180°.
17.答案为:361
18.答案为:28
19.解:(1)第三边为:30﹣a﹣(2a+2)=(28﹣3a)m.
(2)第一条边长不可以为7m.
理由:a=7时,三边分别为7,16,7,
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7m.
18.解:(1)如图1所示:∠ADC=∠BDC=90°;
(2)如图2所示:∠ACD=120°,∠BDC=150°.
20.解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),
∠1+∠DFE=180°(邻补角定义),
∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等两直线平行),
∴∠3=∠ADE(两直线平行内错角相等),
又∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等两直线平行),
∴∠C=∠AED(两直线平行同位角相等).
21.解:∵CD⊥AB,∴∠CDB=90°.
∵∠B=60°,
∴∠BCD=180°-∠CDB-∠B=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠BCE=∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=20°.
22.解:(1)∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|(b+c)-a|+|b-(c+a)|-|c-(a+b)|-|(a+c)-b|
=b+c-a+a+c-b-a-b+c+b-a-c=2c-2a.
(2)∵a+b=11①,b+c=9②,a+c=10③,
∴由①-②,得a-c=2④,由③+④,得2a=12,
∴a=6,∴b=11-6=5,c=10-6=4.
当a=6,b=5,c=4时,原式=2×4-2×6=-4.
23.(1)∵∠=3∠,∠+∠=90°,
∴3∠+∠=90°,∴∠=22.5°.
又∠CAE+∠=90°,∴∠CAE=∠=22.5°.
(2)能,理由如下:
24.解:(1)2∠A=∠1-∠2.
观察图②得:∠1+2∠ADE=180°,2∠AED-∠2=180°,
所以∠1+2∠ADE+2∠AED-∠2=360°.
由三角形内角和是180°得:∠A+∠ADE+∠AED=180°,
所以2∠A+2∠ADE+2∠AED=360°,
所以∠1+2∠ADE+2∠AED-∠2=2∠A+2∠ADE+2∠AED,
所以2∠A=∠1-∠2.
(2)2∠A+2∠D-∠1-∠2=360°.
《认识三角形》专项练习
一 、选择题
1.下列长度的三条线段,能构成三角形的是( )
A.1,2,6 B.1,2,3 C.2,3,4 D.2,2,4
2.一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是( )
A.14 B.15 C.16 D.17
3.在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )
A.1cm<AB<4cm B.5cm<AB<10cm C.4cm<AB<8cm D.4cm<AB<10cm
4.若三角形三个内角的比为1:2:3,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.钝角三角形
5.如图,一个60o角的三角形纸片,剪去这个600角后,得到一个四边形,则么的度数为( )
A.120O B.180O C.240O D.3000
6.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A. B.
C. D.
7.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
8.若a、b、c是△ABC的三边的长,则化简|a-b-c|-|b-c-a|+|a+b-c|=( )
A.a+b+c B.﹣a+3b﹣c C.a+b﹣c D.2b﹣2c
9.如图,在Rt△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A.120° B.108° C.72° D.36°
10.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠DOF=142°,则∠C的度数为( )
A.38° B.39° C.42° D.48°
11.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E.那么∠B等于( )
A.80° B.60° C.40° D.30°
12.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
二 、填空题
13.如图,在△ABC中,AC⊥BC,CD⊥AB于点D.则图中共有_____个直角三角形.
14.已知一个三角形周长是15cm,它的三条边长都是整数,则这个三角形的最长边的最大值是 .
15.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝间距离的最大值为 .
16.如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为 °.
17.对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1(如图所示),记其面积为S1.现再分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2,则S2=_____________.
18.如图,图1中共有3个三角形,图2中共有6个三角形,图3中共有10个三角形,…,以此类推,则图6中共有 __________ 个三角形.
三 、解答题
19.小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.
(1)请用a表示第三条边长.
(2)问第一条边长可以为7m吗?请说明理由.
20.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
21.如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,
求∠BCD和∠ECD的度数.
22.已知a,b,c是三角形的三边长.
(1)化简:|b+c-a|+|b-c-a|-|c-a-b|-|a-b+c|;
(2)在(1)的条件下,若a,b,c满足a+b=11,b+c=9,a+c=10,求这个式子的值.
23.将一副三角板叠放在一起:
(1)如图1,在此种图案的情形下,如果∠ɑ=3∠β,求∠CAE的度数;
(2)如图2,在此种图案的情形下,∠ACE=2∠BCD是否成立?若成立,请求出∠ACD的度数;若不成立,请说明理由.
24.如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置,通过计算我们知道:2∠A=∠l+∠2.请你继续探索:
(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,如图②,此时∠A与∠1、∠2之间存在什么样的关系
(2)如果把四边形ABCD沿时折叠,使点A、D落在四边形BCFE的内部A′、D′的位置,如图③,你能求出∠A、∠D、∠l与∠2之间的关系吗 (直接写出关系式即可)
答案
1.C
2.B
3.B
4.B
5.C.
6.A.
7.D
8.B
9.B
10.A
11.C
12.B
13.答案为:3
14.答案为:5或6或7;
15.答案为:7
16.答案为:180°.
17.答案为:361
18.答案为:28
19.解:(1)第三边为:30﹣a﹣(2a+2)=(28﹣3a)m.
(2)第一条边长不可以为7m.
理由:a=7时,三边分别为7,16,7,
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7m.
18.解:(1)如图1所示:∠ADC=∠BDC=90°;
(2)如图2所示:∠ACD=120°,∠BDC=150°.
20.解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),
∠1+∠DFE=180°(邻补角定义),
∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等两直线平行),
∴∠3=∠ADE(两直线平行内错角相等),
又∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等两直线平行),
∴∠C=∠AED(两直线平行同位角相等).
21.解:∵CD⊥AB,∴∠CDB=90°.
∵∠B=60°,
∴∠BCD=180°-∠CDB-∠B=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠BCE=∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=20°.
22.解:(1)∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|(b+c)-a|+|b-(c+a)|-|c-(a+b)|-|(a+c)-b|
=b+c-a+a+c-b-a-b+c+b-a-c=2c-2a.
(2)∵a+b=11①,b+c=9②,a+c=10③,
∴由①-②,得a-c=2④,由③+④,得2a=12,
∴a=6,∴b=11-6=5,c=10-6=4.
当a=6,b=5,c=4时,原式=2×4-2×6=-4.
23.(1)∵∠=3∠,∠+∠=90°,
∴3∠+∠=90°,∴∠=22.5°.
又∠CAE+∠=90°,∴∠CAE=∠=22.5°.
(2)能,理由如下:
24.解:(1)2∠A=∠1-∠2.
观察图②得:∠1+2∠ADE=180°,2∠AED-∠2=180°,
所以∠1+2∠ADE+2∠AED-∠2=360°.
由三角形内角和是180°得:∠A+∠ADE+∠AED=180°,
所以2∠A+2∠ADE+2∠AED=360°,
所以∠1+2∠ADE+2∠AED-∠2=2∠A+2∠ADE+2∠AED,
所以2∠A=∠1-∠2.
(2)2∠A+2∠D-∠1-∠2=360°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
