人教版数学七年级下册8.3实际问题与二元一次方程组(几何问题)课后练习(含解析)
文档属性
| 名称 | 人教版数学七年级下册8.3实际问题与二元一次方程组(几何问题)课后练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 905.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 20:50:34 | ||
图片预览

文档简介
实际问题与二元一次方程组
几何问题
一、单选题
1.如图,七个相同的小长方形组成一个大长方形,若,则小长方形的面积为( )
A.80 B.90 C.610 D.630
2.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒、现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则的值可能是( )
A.2025 B.2024 C.2023 D.2022
3.小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为的小正方形,则每个小长方形的长和宽分别为( )
A. B. C. D.
4.用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图①所示的正方形,其阴影部分的面积为81,8个长方形纸片围成如图②所示的正方形,其阴影部分的面积为64,12个长方无纸片围成如图③所示的正方形,其阴影部分的面积为( )
A.48 B.36 C.50 D.49
5.如图,将7张相同的长方形纸片不重叠的放在长方形内,已知小长方形纸片的长为a,宽为b,且,若未被覆盖的两个长方形周长相等,则( )
A. B. C. D.
6.在长方形中,放入6个形状大小完全相同的小长方形,所标尺寸如图所示,则小长方形的宽的长度为( ).
A.0 B. C.2 D.
7.足球一般是用黑白两种颜色的皮块缝制而成的,如图所示.黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,设黑色皮块和白色皮块的块数依次为x和y,可列方程是( )
A. B. C. D.
8.一个大正方形和四个相同的小正方形按图1,图2所示两种方式摆放,则大正方形的边长是 ( )
A. B.
C. D.
9.如图,利用两个外形一致的长方形木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.81cm B.83cm C.85cm D.87cm
10.剪纸艺术是中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点E的坐标为,其关于y轴对称的点F的坐标为,则的值为( )
A. B. C.1 D.0
11.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为55cm,此时木桶中水的深度是( )
A.16 B.18 C.20 D.24
12.如图,在长为30米,宽为20米的长方形花园里,原有两条面积相等的小路,其余部分绿化.现在为了增加绿地面积,把公园里的一条小路改为绿地,只保留另一条小路,并且使得绿地面积是小路面积的4倍,则x与y的值分别为( )
A.3,2 B.5,4 C.6,5 D.6,4
二、填空题
13.一个长方形的长减少7cm,宽增加3cm,就成为一个正方形,并且这两个图形的面积相等.则这个长方形的宽为______cm.
14.如图,把两个形状和大小都一样的小长方形边框(厚度忽略不计)摆成形,已知,,则一个小长方形面积为______.
15.如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30cm,两块竖放的墙砖比两块横放的墙砖高50cm,则每块墙砖的截面面积是_______________cm2.
16.利用两块完全相同的直角三角板测量升旗台的高度.首先将两块完全相同的三角板按图1放置,然后交换两块三角板的位置,按图2放置,测量数据如图所示,则升旗台的高度是___________cm.
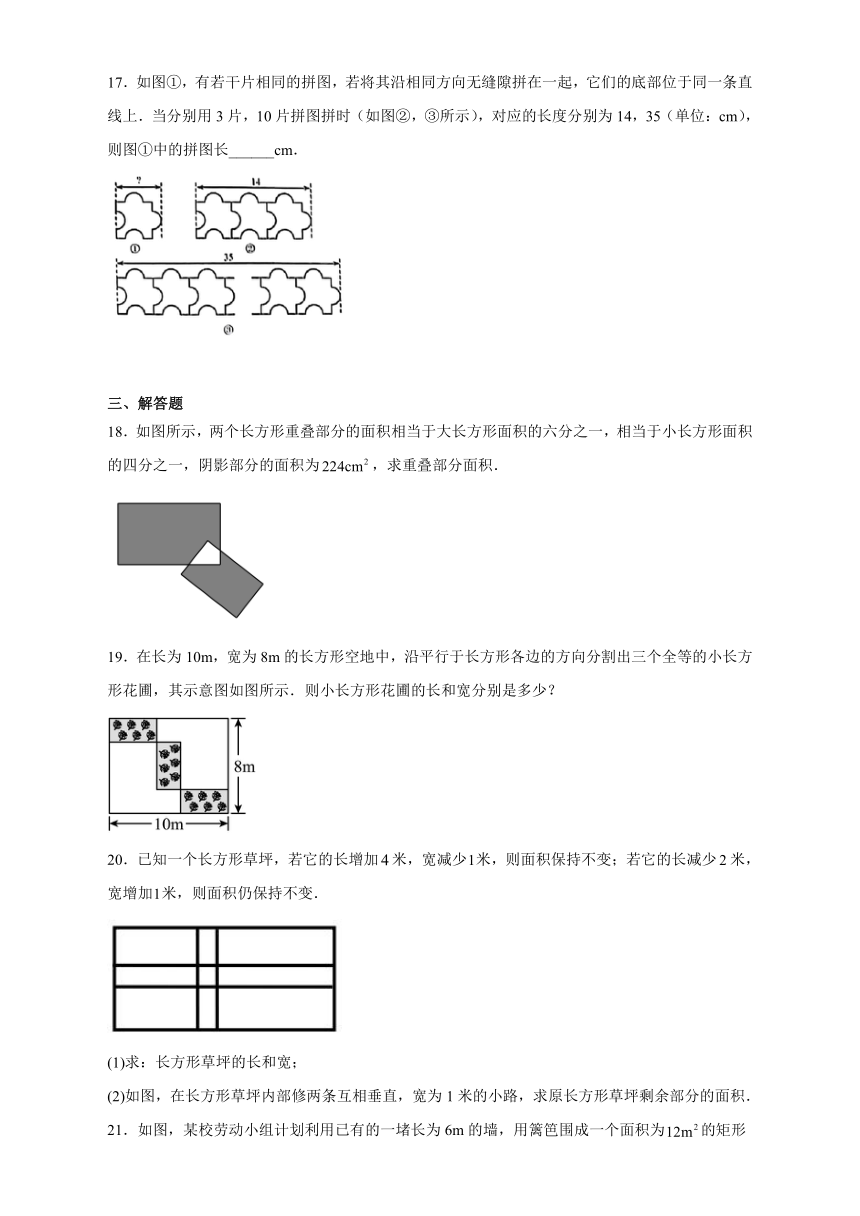
17.如图①,有若干片相同的拼图,若将其沿相同方向无缝隙拼在一起,它们的底部位于同一条直线上.当分别用3片,10片拼图拼时(如图②,③所示),对应的长度分别为14,35(单位:cm),则图①中的拼图长______cm.
三、解答题
18.如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为,求重叠部分面积.
19.在长为10m,宽为8m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别是多少?
20.已知一个长方形草坪,若它的长增加米,宽减少米,则面积保持不变;若它的长减少米,宽增加米,则面积仍保持不变.
(1)求:长方形草坪的长和宽;
(2)如图,在长方形草坪内部修两条互相垂直,宽为1米的小路,求原长方形草坪剩余部分的面积.
21.如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地ABCD,边AD的长不超过墙的长度,在BC边上开设宽为1m的门EF(门不需要消耗篱笆).设AB的长为x(m),BC的长为y(m).
(1)若围成矩形劳动基地ABCD三边的篱笆总长为10m,求AB和BC的长度.
(2)若AB和BC的长都是整数(单位:m),且围成矩形劳动基地ABCD三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.
22.(1)如图1,宽为48cm的长方形由8个形状、大小相同的小长方形拼成,其中一个小长方形的面积为______;
(2)如图1,图2,都是由8个形状、大小相同的小长方形拼(围)成的大矩形,且图2中的阴影部分(小矩形)的面积为,则小长方形的长为______cm;
(3)如图3,在长方形中放置9个形状、大小相同的小长方形,求所有阴影部分面积的和.(说明:图中的单位为cm)
23.某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图所示,(单位:cm)
(1)列出方程(组),求出图甲中a与b的值______.
(2)在试生产阶段,若将m张标准板材用裁法一裁剪,n张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式无盖礼品盒.
①两种裁法共产生A型板材______张,B型板材______张(用m、n的代数式表示);
②当时,所裁得的A型板材和B型板材恰好用完,做成的横式无盖礼品盒可能是______个.(在横线上直接写出所有可能答案,无需书写过程)
参考答案
1.B
解:设小长方形的长为x,宽为y,
根据题意得:,
解得:,
∴,
∴小长方形的面积为90.
故选:B.
2.A
解:设可以做竖式纸盒x个,横式纸盒y个,
由题意可得:
∴,
由于x,y均为整数,故为5的倍数,
选项中只有2025是5的倍数.
故选A.
3.C
解:设每个长方形的长为,宽为,
由题意,得,
解得:,
∴每个小长方形的长为,宽为.
故选:C.
4.D
解:图①中阴影面积是81,边长为9,图②阴影面积是64,边长为8,设矩形长为a,宽为b,根据题意得:
解得:,
所以图③阴影面积为:,
故选:D.
5.C
解:依题意,小长方形纸片的长为a,宽为b,
如图所示,
的周长为:,
的周长为:,
的周长与的周长相等,
,
,
,
故选:C.
6.C
解:设小长方形的长为,宽为,则,,
即,
根据题意,得
,解得,
即,
故选:C.
7.D
解:设黑色皮块和白色皮块的块数依次为x和y,由题意得
.
故选D.
8.A
解:设大正方形的边长为,小正方形的边长为,由图①和②列出方程组得:
,
解得,
∴大正方形的边长为,故A正确.
故选:A.
9.C
解:设桌子的高度为xcm,长方体木块的长比宽长ycm,
根据题意得:,
解得:.
故选:C
10.C
解:∵,关于y轴对称,
∴,
解得,,
∴
故选:C.
11.C
解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm,根据题意得,
解得:
因此木桶中水的深度为(cm).
故选:C.
12.D
解:根据题意可知,,
解得:,故D正确.
故选:D.
13.
解:设这个长方形的长为x cm,宽为y cm,
由题意可得:,即
解得:,
这个长方形的长为cm,宽为cm,
故答案为:.
14.
解:设小长方形的长和宽分别为x,y,
由题意得,,
解得,
∴长方形的面积为,
故答案为:.
15.900
解:设每块墙砖的长为,宽为,
依题意得:,
解得:,
.
故答案为:900.
16.69
解:设升旗台的高度是,三角板的较长直角边长为,较小直角边长为,
则,
解得:
故答案为:.
17.8
解:
如图,设每个拼图的长由x和y两部分组成,则根据图二和图三可列出两个方程:
解得:
所以拼图长为:
故答案为:8
18.
解:设大长方形的面积为,小长方形的面积为,根据题意得,
解得:
∴重叠面积为
19.小长方形花圃的长为4m,宽为2m
解:设小长方形花圃的长为,宽为,
由题意得,
解得.
答:小长方形花圃的长为,宽为.
20.(1)长方形草坪的长为米,宽为米
(2)原长方形草坪剩余部分的面积为14平方米
(1)解:设长方形草坪的长和宽分别为米,根据题意,得
即
解得:
答:长方形草坪的长为米,宽为米
(2)解:依题意,平方米,
答:原长方形草坪剩余部分的面积为14平方米.
21.(1)AB=4,BC=3
(2)AB=2,BC=6或AB=3,BC=4
解:(1)根据题意得:,即.
代入得:,整理得:.
解得:或.
当时,,不符合题意;当时,,符合题意.
则AB=4,BC=3.
(2)根据题意得:,即.
∵AB,BC为整数,即x,y为整数,且.
∴当y=6时,x=2;当y=4时,x=3.
则满足条件的围建方案为:AB=2,BC=6或AB=3,BC=4.
22.(1)540;(2)5;(3)738
解:(1)设这8个大小一样的小长方形的长为,宽为.
,
解得,
∴一个小长方形的面积为,
故答案为:540;
(2)设这8个大小一样的小长方形的长为,宽为,由图可知,中间小正方形是边长为的小正方形,
,
解得,
∴小长方形的长为5cm;
故答案为:5;
(3)设小长方形宽为,长为,
由图可知大长方形长为,宽为,
则,
解得,
∴大长方形的宽为48cm,
所有阴影部分面积的和.
23.(1)
(2)①;;②24,27,30
解:(1)由题意得:,
解得;
故答案为:60,40;
(2)①由图示裁法一产生A型板材为:2×m=2m,裁法二产生A型板材为:1×n=n,
所以两种裁法共产生A型板材为2m+n(张),
由图示裁法一产生B型板材为:1×m=m,裁法二产生A型板材为,2×n=2n,
所以两种裁法共产生B型板材为(m+2n)张;
故答案为:2m+n;m+2n;
②当30≤m≤40时,所裁得的A型板材和B型板材恰好用完,做成的横式无盖礼品盒可能是24或27或30个.
由图可知,做一个横式无盖礼品盒需A型板材3张,B型板材2张.
∵所裁得的板材恰好用完,
∴,化简得m=4n.
∵n,m皆为整数,
∴m为4的整数倍,
又∵30≤m≤40,
∴m可取32,36,40,
此时,n分别为8,9,10,可做成的礼品盒个数分别为24,27,30.
故答案为: 24或27或30.
几何问题
一、单选题
1.如图,七个相同的小长方形组成一个大长方形,若,则小长方形的面积为( )
A.80 B.90 C.610 D.630
2.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒、现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则的值可能是( )
A.2025 B.2024 C.2023 D.2022
3.小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为的小正方形,则每个小长方形的长和宽分别为( )
A. B. C. D.
4.用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图①所示的正方形,其阴影部分的面积为81,8个长方形纸片围成如图②所示的正方形,其阴影部分的面积为64,12个长方无纸片围成如图③所示的正方形,其阴影部分的面积为( )
A.48 B.36 C.50 D.49
5.如图,将7张相同的长方形纸片不重叠的放在长方形内,已知小长方形纸片的长为a,宽为b,且,若未被覆盖的两个长方形周长相等,则( )
A. B. C. D.
6.在长方形中,放入6个形状大小完全相同的小长方形,所标尺寸如图所示,则小长方形的宽的长度为( ).
A.0 B. C.2 D.
7.足球一般是用黑白两种颜色的皮块缝制而成的,如图所示.黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,设黑色皮块和白色皮块的块数依次为x和y,可列方程是( )
A. B. C. D.
8.一个大正方形和四个相同的小正方形按图1,图2所示两种方式摆放,则大正方形的边长是 ( )
A. B.
C. D.
9.如图,利用两个外形一致的长方形木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.81cm B.83cm C.85cm D.87cm
10.剪纸艺术是中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点E的坐标为,其关于y轴对称的点F的坐标为,则的值为( )
A. B. C.1 D.0
11.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为55cm,此时木桶中水的深度是( )
A.16 B.18 C.20 D.24
12.如图,在长为30米,宽为20米的长方形花园里,原有两条面积相等的小路,其余部分绿化.现在为了增加绿地面积,把公园里的一条小路改为绿地,只保留另一条小路,并且使得绿地面积是小路面积的4倍,则x与y的值分别为( )
A.3,2 B.5,4 C.6,5 D.6,4
二、填空题
13.一个长方形的长减少7cm,宽增加3cm,就成为一个正方形,并且这两个图形的面积相等.则这个长方形的宽为______cm.
14.如图,把两个形状和大小都一样的小长方形边框(厚度忽略不计)摆成形,已知,,则一个小长方形面积为______.
15.如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30cm,两块竖放的墙砖比两块横放的墙砖高50cm,则每块墙砖的截面面积是_______________cm2.
16.利用两块完全相同的直角三角板测量升旗台的高度.首先将两块完全相同的三角板按图1放置,然后交换两块三角板的位置,按图2放置,测量数据如图所示,则升旗台的高度是___________cm.
17.如图①,有若干片相同的拼图,若将其沿相同方向无缝隙拼在一起,它们的底部位于同一条直线上.当分别用3片,10片拼图拼时(如图②,③所示),对应的长度分别为14,35(单位:cm),则图①中的拼图长______cm.
三、解答题
18.如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为,求重叠部分面积.
19.在长为10m,宽为8m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别是多少?
20.已知一个长方形草坪,若它的长增加米,宽减少米,则面积保持不变;若它的长减少米,宽增加米,则面积仍保持不变.
(1)求:长方形草坪的长和宽;
(2)如图,在长方形草坪内部修两条互相垂直,宽为1米的小路,求原长方形草坪剩余部分的面积.
21.如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地ABCD,边AD的长不超过墙的长度,在BC边上开设宽为1m的门EF(门不需要消耗篱笆).设AB的长为x(m),BC的长为y(m).
(1)若围成矩形劳动基地ABCD三边的篱笆总长为10m,求AB和BC的长度.
(2)若AB和BC的长都是整数(单位:m),且围成矩形劳动基地ABCD三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.
22.(1)如图1,宽为48cm的长方形由8个形状、大小相同的小长方形拼成,其中一个小长方形的面积为______;
(2)如图1,图2,都是由8个形状、大小相同的小长方形拼(围)成的大矩形,且图2中的阴影部分(小矩形)的面积为,则小长方形的长为______cm;
(3)如图3,在长方形中放置9个形状、大小相同的小长方形,求所有阴影部分面积的和.(说明:图中的单位为cm)
23.某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图所示,(单位:cm)
(1)列出方程(组),求出图甲中a与b的值______.
(2)在试生产阶段,若将m张标准板材用裁法一裁剪,n张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式无盖礼品盒.
①两种裁法共产生A型板材______张,B型板材______张(用m、n的代数式表示);
②当时,所裁得的A型板材和B型板材恰好用完,做成的横式无盖礼品盒可能是______个.(在横线上直接写出所有可能答案,无需书写过程)
参考答案
1.B
解:设小长方形的长为x,宽为y,
根据题意得:,
解得:,
∴,
∴小长方形的面积为90.
故选:B.
2.A
解:设可以做竖式纸盒x个,横式纸盒y个,
由题意可得:
∴,
由于x,y均为整数,故为5的倍数,
选项中只有2025是5的倍数.
故选A.
3.C
解:设每个长方形的长为,宽为,
由题意,得,
解得:,
∴每个小长方形的长为,宽为.
故选:C.
4.D
解:图①中阴影面积是81,边长为9,图②阴影面积是64,边长为8,设矩形长为a,宽为b,根据题意得:
解得:,
所以图③阴影面积为:,
故选:D.
5.C
解:依题意,小长方形纸片的长为a,宽为b,
如图所示,
的周长为:,
的周长为:,
的周长与的周长相等,
,
,
,
故选:C.
6.C
解:设小长方形的长为,宽为,则,,
即,
根据题意,得
,解得,
即,
故选:C.
7.D
解:设黑色皮块和白色皮块的块数依次为x和y,由题意得
.
故选D.
8.A
解:设大正方形的边长为,小正方形的边长为,由图①和②列出方程组得:
,
解得,
∴大正方形的边长为,故A正确.
故选:A.
9.C
解:设桌子的高度为xcm,长方体木块的长比宽长ycm,
根据题意得:,
解得:.
故选:C
10.C
解:∵,关于y轴对称,
∴,
解得,,
∴
故选:C.
11.C
解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm,根据题意得,
解得:
因此木桶中水的深度为(cm).
故选:C.
12.D
解:根据题意可知,,
解得:,故D正确.
故选:D.
13.
解:设这个长方形的长为x cm,宽为y cm,
由题意可得:,即
解得:,
这个长方形的长为cm,宽为cm,
故答案为:.
14.
解:设小长方形的长和宽分别为x,y,
由题意得,,
解得,
∴长方形的面积为,
故答案为:.
15.900
解:设每块墙砖的长为,宽为,
依题意得:,
解得:,
.
故答案为:900.
16.69
解:设升旗台的高度是,三角板的较长直角边长为,较小直角边长为,
则,
解得:
故答案为:.
17.8
解:
如图,设每个拼图的长由x和y两部分组成,则根据图二和图三可列出两个方程:
解得:
所以拼图长为:
故答案为:8
18.
解:设大长方形的面积为,小长方形的面积为,根据题意得,
解得:
∴重叠面积为
19.小长方形花圃的长为4m,宽为2m
解:设小长方形花圃的长为,宽为,
由题意得,
解得.
答:小长方形花圃的长为,宽为.
20.(1)长方形草坪的长为米,宽为米
(2)原长方形草坪剩余部分的面积为14平方米
(1)解:设长方形草坪的长和宽分别为米,根据题意,得
即
解得:
答:长方形草坪的长为米,宽为米
(2)解:依题意,平方米,
答:原长方形草坪剩余部分的面积为14平方米.
21.(1)AB=4,BC=3
(2)AB=2,BC=6或AB=3,BC=4
解:(1)根据题意得:,即.
代入得:,整理得:.
解得:或.
当时,,不符合题意;当时,,符合题意.
则AB=4,BC=3.
(2)根据题意得:,即.
∵AB,BC为整数,即x,y为整数,且.
∴当y=6时,x=2;当y=4时,x=3.
则满足条件的围建方案为:AB=2,BC=6或AB=3,BC=4.
22.(1)540;(2)5;(3)738
解:(1)设这8个大小一样的小长方形的长为,宽为.
,
解得,
∴一个小长方形的面积为,
故答案为:540;
(2)设这8个大小一样的小长方形的长为,宽为,由图可知,中间小正方形是边长为的小正方形,
,
解得,
∴小长方形的长为5cm;
故答案为:5;
(3)设小长方形宽为,长为,
由图可知大长方形长为,宽为,
则,
解得,
∴大长方形的宽为48cm,
所有阴影部分面积的和.
23.(1)
(2)①;;②24,27,30
解:(1)由题意得:,
解得;
故答案为:60,40;
(2)①由图示裁法一产生A型板材为:2×m=2m,裁法二产生A型板材为:1×n=n,
所以两种裁法共产生A型板材为2m+n(张),
由图示裁法一产生B型板材为:1×m=m,裁法二产生A型板材为,2×n=2n,
所以两种裁法共产生B型板材为(m+2n)张;
故答案为:2m+n;m+2n;
②当30≤m≤40时,所裁得的A型板材和B型板材恰好用完,做成的横式无盖礼品盒可能是24或27或30个.
由图可知,做一个横式无盖礼品盒需A型板材3张,B型板材2张.
∵所裁得的板材恰好用完,
∴,化简得m=4n.
∵n,m皆为整数,
∴m为4的整数倍,
又∵30≤m≤40,
∴m可取32,36,40,
此时,n分别为8,9,10,可做成的礼品盒个数分别为24,27,30.
故答案为: 24或27或30.
