球[上学期]

课件24张PPT。高中立体几何多媒体课件球西伯利亚 2.5 球 ----主页例题讲解地球经纬本课小结巩固练习直观画球教学目标球的概念球面距离球的性质课堂练习单击按钮进入各个教学环节教学目标A(识记) 1.球的概念和性质。
2.球的截面图形是圆及其性质。
3.大圆、小圆的定义 。
4.球面上两点距离的定义。
5.会画球的直观图。
B(领会) 1.球的截面图形是圆.
2.能将球的有关问题转化为圆的有
关问题来考虑。
3.能说明地球经、纬度的含义。
C(应用) 1.能用球的概念、性质解答问题。
2.能解决球面的两点距离和球心到
截面距离问题。
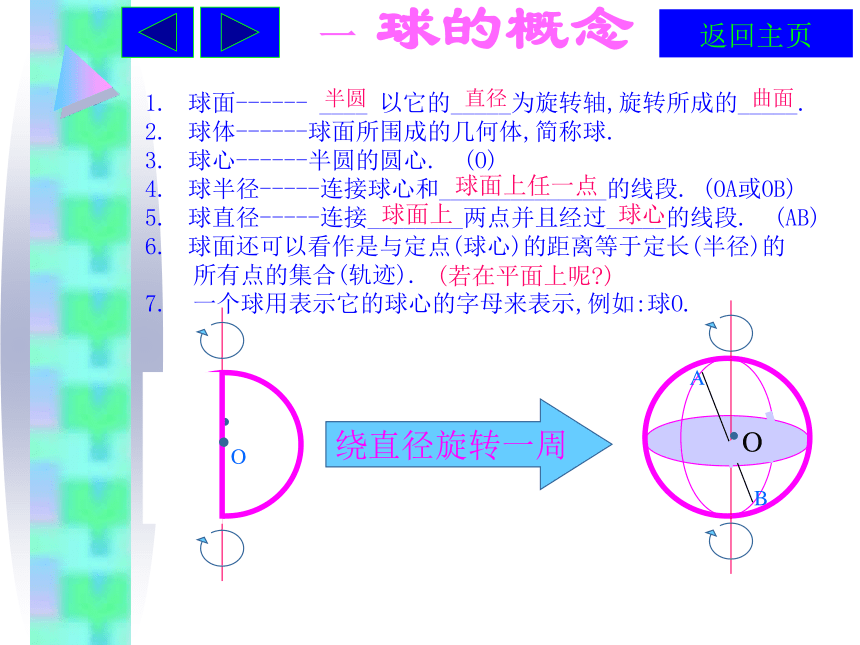
返回主页球面------ ____ 以它的_____为旋转轴,旋转所成的_____.
球体------球面所围成的几何体,简称球.
球心------半圆的圆心. (O)
球半径-----连接球心和______________的线段. (OA或OB)
球直径-----连接________两点并且经过_____的线段. (AB)
球面还可以看作是与定点(球心)的距离等于定长(半径)的
所有点的集合(轨迹).
7. 一个球用表示它的球心的字母来表示,例如:球O.一 球的概念绕直径旋转一周 O ...O半圆直径曲面 球面上任一点球面上球心(若在平面上呢?)AB返回主页二 球的截面及其性质现在，我们用一个平面去截一个球, 是
球的截面的性质:
1.球心和截面圆心的连线 于截面.
2.球心到截面的距离 与球的半径 ,
下面的关系:
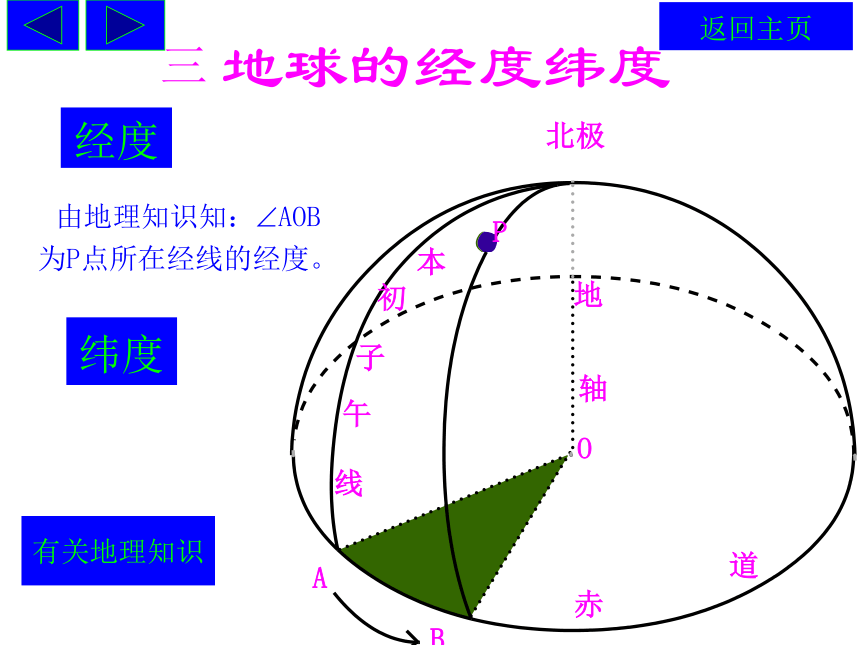
O?圆面.什么图形呢？截面 垂直返回主页三 地球的经度纬度经度有关地理知识由地理知识知：?AOB
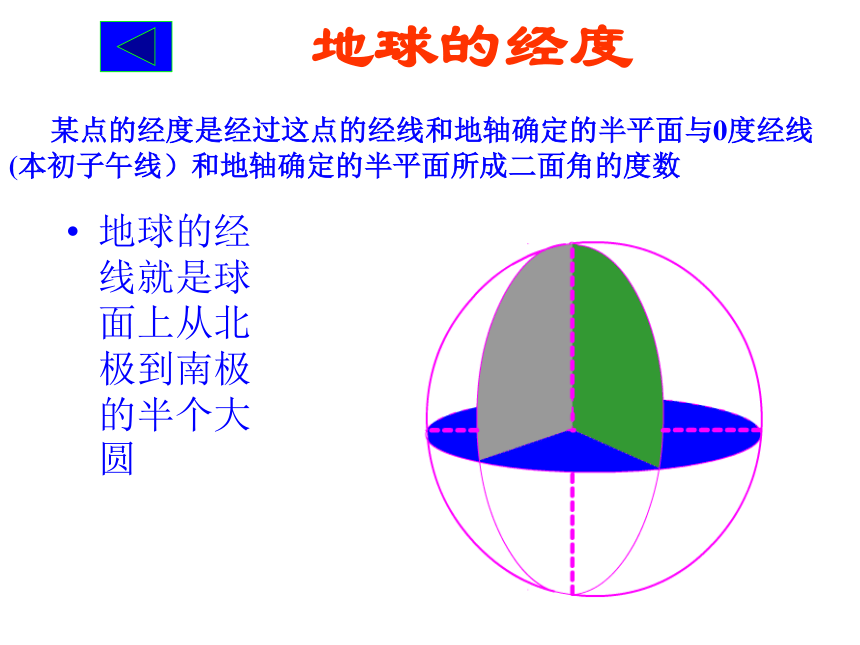
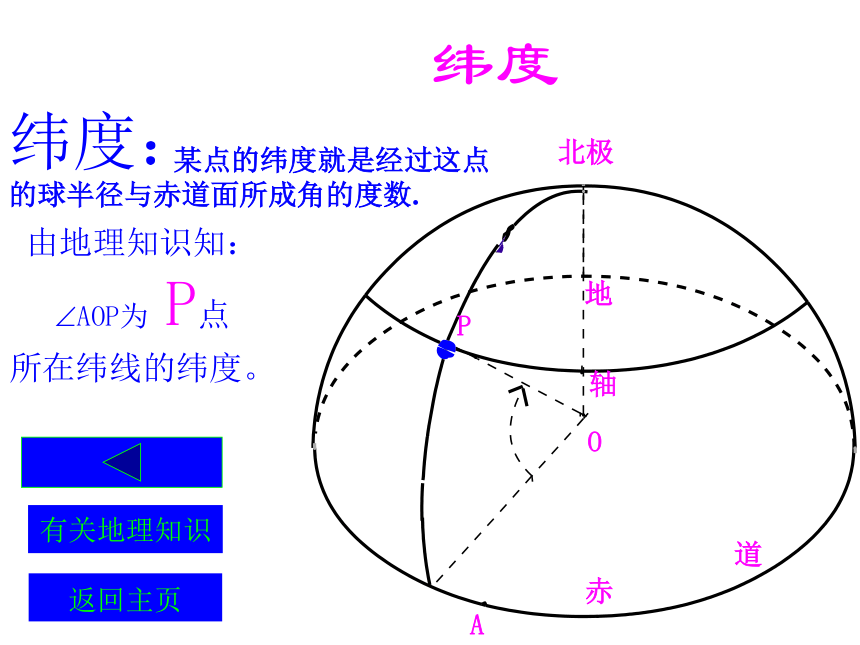
为P点所在经线的经度。纬度返回主页地球的经度地球的经线就是球面上从北极到南极的半个大圆 某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线）和地轴确定的半平面所成二面角的度数纬度纬度：由地理知识知： ?AOP为 P点
所在纬线的纬度。有关地理知识返回主页 某点的纬度就是经过这点
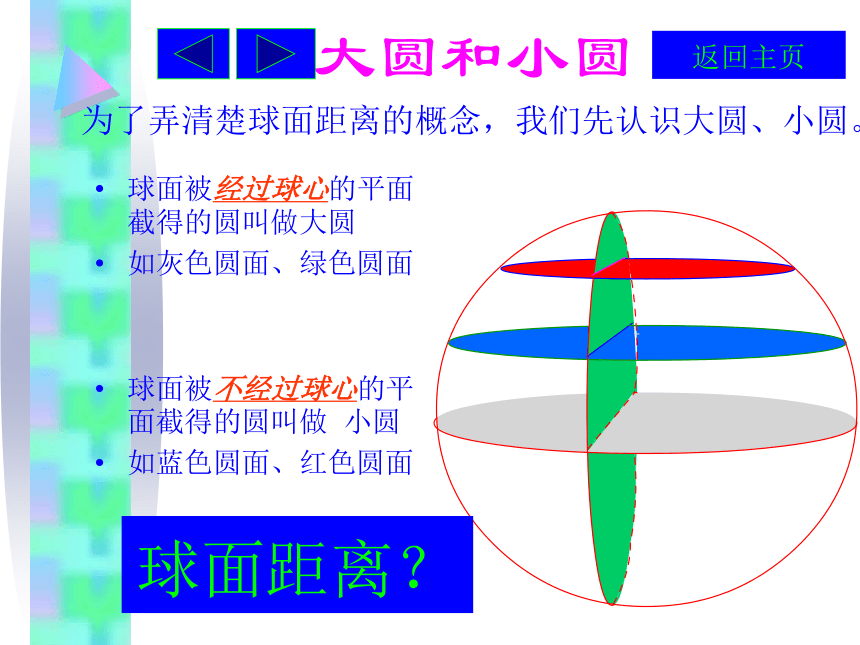
的球半径与赤道面所成角的度数.大圆和小圆球面被经过球心的平面截得的圆叫做大圆
如灰色圆面、绿色圆面
球面被不经过球心的平面截得的圆叫做 小圆
如蓝色圆面、红色圆面球面距离？为了弄清楚球面距离的概念，我们先认识大圆、小圆。返回主页球面距离返回主页在球面上两点
之间的最段距离
就是经过这两点
的大圆在这两点
间的劣弧的长度
——这个弧长叫
两点的球面距离。球的截面形状如右图：
用红、蓝、灰、绿
四个不同颜色
的平面去截球
得到红、蓝、
灰、绿四个
圆形截面。返回球的直观图作法画轴：经过点O画x轴y轴z轴,轴间角为120 画大圆：以O为中心分别按x轴、y轴,y轴、
z轴,z轴、x轴画半径为R的圆
的直观图（三个椭圆）
成图：以点O为圆心画一个圆与三个椭圆都相切
返回主页我国首都北京靠近北纬40度，球北纬40度纬线的长度（地球半径约是6370km)解答例题1返回主页解答如图：
设纬线的圆心为D点，DP为纬线半径
∴ OD⊥DP
∵?DPO= ? POB=40°，
∴DP=OP×cos ? OPD
∴纬线长=2? × DP
= 2 ? × OP × cos40 °
≈2 × 3.14 × 6370 × 0.766 ≈30660(km)
返回练习1 1.设地球的半径为R，在北纬30 °圈上有甲乙两地，它们的经度相差120 ° ，那么这两地的纬线的长为___________参考答案2.设地球的半径为R，在北纬30 °圈上有A、B
两点，它们的经度相差180 ° ，则A、B两点的
球面距离是___________
3.过球面上两点可作一个且只能作一个大圆 ( )4.垂直于球的半径的平面是这个球的切面 ( )5.过球面上任意两点都有无数个小圆 ( )练习2做《掌握学习指导》p58 ：T 1、2
返回主页p62 : T1 参考答案：1（1）半经为r的圆。（2）半径为r的球面。
（3）半径为r的球体。
2
o1oA答案是：由 R2-R2/4=(9??10)2 可得 R=34.6cm返回主页提示1 由纬线圈上的弧长求得AB的弦长,再求AB所对的大圆中心角,最后再求球面距离.
2 (略)返回主页参考答案1. ∵ AK=OK ×cos30 °
=
∴甲乙长=1/3×2 AK
= R/3
2. ∵∴又AB的球面距即大圆ABP上的劣弧ACB的长
即1/3大圆周长
即为2 R/3返回主页 本课小结本节课主要学习了:返回主页1.球的概念和性质
2.大圆、小圆、球面上两点的距离的定义
3.球的截面为圆面及这个截面的两个性质
4.地球经纬度的含义
5.球的直观图作法
结束今天的作业:教材P96 T2,3That’s all !证明∵OD=OA，DK=KA
∴OK⊥DA
同理OK ⊥BC
∴OK⊥面ABCD返回地理知识返回经度返回纬度结束