福建省厦门市五显中学2022-2023学年高二下学期期中考试数学试题(含答案)
文档属性
| 名称 | 福建省厦门市五显中学2022-2023学年高二下学期期中考试数学试题(含答案) | 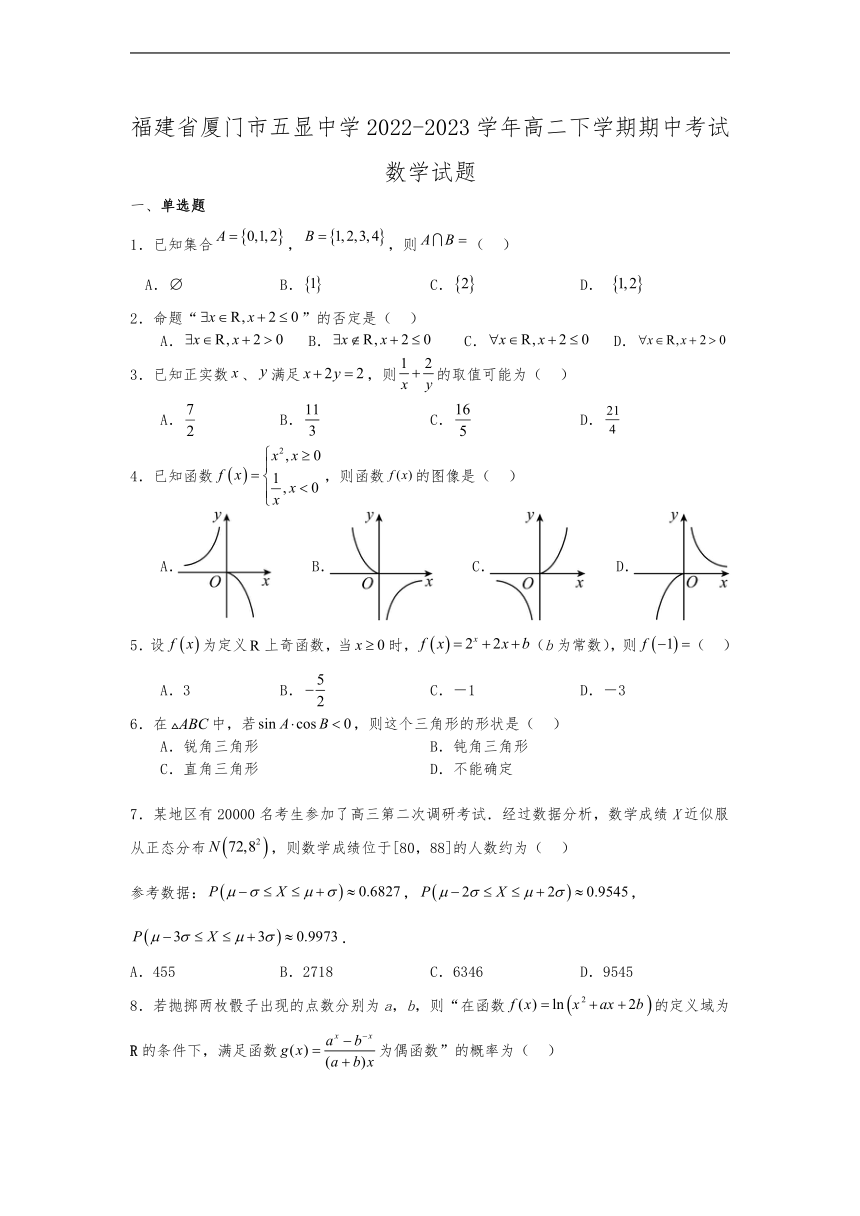 | |
| 格式 | docx | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 10:21:39 | ||
图片预览




文档简介
福建省厦门市五显中学2022-2023学年高二下学期期中考试数学试题
单选题
1.已知集合,,则( )
A. B. C. D.
2.命题“”的否定是( )
A. B. C. D.
3.已知正实数、满足,则的取值可能为( )
A. B. C. D.
4.已知函数,则函数的图像是( )
A. B. C. D.
5.设为定义上奇函数,当时,(b为常数),则( )
A.3 B. C.-1 D.-3
6.在中,若,则这个三角形的形状是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
7.某地区有20000名考生参加了高三第二次调研考试.经过数据分析,数学成绩X近似服从正态分布,则数学成绩位于[80,88]的人数约为( )
参考数据:,,.
A.455 B.2718 C.6346 D.9545
8.若抛掷两枚骰子出现的点数分别为a,b,则“在函数的定义域为R的条件下,满足函数为偶函数”的概率为( )
A. B. C. D.
二、多选题
9.下列叙述中不正确的是( )
A.若,则“不等式恒成立”的充要条件是“”;
B.若,则“”的充要条件是“”;
C.“”是“方程有一个正根和一个负根”的必要不充分条件;
D.“”是“”的充分不必要条件.
10.给出下列四个命题,其中是真命题的为( )
A.如果θ是第一或第四象限角,那么
B.如果,那么θ是第一或第四象限角
C.终边在x轴上的角的集合为
D.已知扇形OAB的面积为1,周长为4,则扇形的圆心角(正角)的弧度数为2
11.下列说法正确的有( )
A.若事件与事件互斥,则事件与事件对立
B.若随机变量,则方差
C.若随机变量,,则
D.以模型去拟合一组数据时,为了求出回归方程,设,求得线性回归方程为,则的值分别是和
12.乒乓球,被称为中国的“国球”.某次比赛采用五局三胜制,当参赛甲 乙两位中有一位赢得三局比赛时,就由该选手晋级而比赛结束.每局比赛皆须分出胜负,且每局比赛的胜负不受之前比赛结果影响.假设甲在任一局赢球的概率为,实际比赛局数的期望值记为,则下列说法中正确的是( )
A.三局就结束比赛的概率为 B.的常数项为3
C.函数在上单调递减 D.
三、填空题
13.已知函数,则方程的解为________.
14.已知,则__________.
15.已知函数的极小值为2,则______
16.2021年11月27日奥密克戎毒株输入我国香港,某医院委派甲、乙、丙、丁四名医生前往三个小区做好防疫工作,每个小区至少委派一名医生,在甲派往小区的条件下,乙派往小区的概率为____.
四、解答题
17.已知函数.
(1)当时,求值; (2)若是偶函数,求的最大值.
18.设集合,.
(1)若,求;
(2)当时,求实数的取值范围.
19.已知-<x<0,sin x+cos x=.
(1)求sinxcosx; (2)求sinx-cosx的值
20.某校为了丰富学生课余生活,组建了足球社团.为了解学生喜欢足球是否与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
喜欢足球 不喜欢足球 合计
男生 40
女生 30
合计
(1)根据所给数据完成上表,依据的独立性检验,能否认为该校学生喜欢足球与性别有关?
(2)社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知这两名男生进球的概率均为,这名女生进球的概率为,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.
附:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
21.某企业有甲、乙两个研发小组,甲组研究新产品成功的概率为,乙组研究新产品成功的概率为,现安排甲组研发新产品,乙组研发新产品,设甲、乙两组的研发相互独立.
(1)求恰好有一种新产品研发成功的概率;
(2)若新产品研发成功,预计企业可获得利润120万元,不成功则会亏损50万元;若新产品研发成功,企业可获得利润100万元,不成功则会亏损40万元,求该企业获利万元的分布列.
22.已知函数.
(1)若的图象在处的切线与直线垂直,求实数的值;
(2)讨论在上的单调性.
22-23学年下高二期中数学试题(第 4页,共 4 页)
2022-2023学年(下)厦门市五显中学高二年期中试卷数学学科参考答案:
1.D 2.D 3.D 4.C 5.D 6.B
7.B【详解】由题意可知,,
则数学成绩位于[80,88]的人数约为.故选:B
8.B【详解】抛掷两枚骰子出现的点数分别为a,b,共36种情况,如下
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
记函数的定义域为R为事件A,
即恒成立,需满足,即,
满足的有26种情况,故.
记函数为偶函数为事件B,
函数的定义域为,由偶函数的定义知,即或.
满足或的有6种情况,故,
故,故选:B
9.AB 10.AD
11.BCD【详解】由对立事件和互斥事件定义可得,对立事件是互斥的,互斥事件不一定对立,所以A选项错误;
由二项分布可得,又由公式可得
,所以B选项正确;
正态分布,对称轴, ,
得,又因为与关于对称,所以,所以C选项正确;
将两边同时取得,,与对应,
则,即,,所以D选项正确.故选:BCD
12.ABD【详解】设实际比赛局数为,则的可能取值为,
所以,,
,因此三局就结束比赛的概率为,则A正确;
故
, 由知常数项为3,故B正确;
由,故D正确;
由,
,所以,
令,则;令,则,
则函数在上单调递增,则C不正确.故选:ABD.
13.1 14. 15.
16.【详解】记事件为“甲派往小区”,事件为“乙派往小区”,则
若A小区分配甲一个人,则有,若A小区分配甲以及另一个人一起,则有,故事件包含的基本事件个数为,
在甲派往小区的条件下,乙派往小区的情况为:①只有甲派往小区,只有乙派往小区,另外两个人去C小区,则有1种情况,②从丙丁中选一个人连同甲一起派往小区,只有乙派往小区,剩下一个人去C小区,则有种情况,③从丙丁中选一个人连同乙一起派往小区,只有甲派往小区,剩下一个人去C小区,则有种情况,
,故答案为:
17.解:当时,,所以;
(2)因为是偶函数,所以成立,
即成立,
所以,则,所以的最大值为2.
18.【详解】(1)因为,所以集合
集合,所以,
所以
(2)因为,所以,所以,解得.
19.(1)由sin x+cos x=两边平方得,
所以.
(2)因为-<x<0,所以,,
所以
20.【详解】(1)列联表如下:
喜欢足球 不喜欢足球 合计
男生 60 40 100
女生 30 70 100
合计 90 110 200
则,
所以依据的独立性检验,能认为该校学生喜欢足球与性别有关.
(2)依题意得3人进球总次数的所有可能取值为,
,,
,,
所以的分布列如下:
0 1 2 3
所以的数学期望为.
21.(1)因为甲、乙两个研发小组研究新产品成功的概率分别为为和,且相互独立,
所以,恰好有一种新产品研发成功的概率;
(2)根据题意,的可能取值有.
,
所以分布列为:
22.(1)由题知,,,解得.
(2)
(i)当时,若,则,
若,此时开口向下,对称轴为,
所以当时,,
在单调递减;
(ii)当时,开口向上,,
则(根据二次函数大致图象知舍去)
且当时,单调递减;
当时,单调递增.
(iii)当时,开口向上,对称轴在单调递增,
当时,在单调递增.
综上:当时,在单调递减;
当时,在单调递减,在单调递增,
当时,在单调递增.
单选题
1.已知集合,,则( )
A. B. C. D.
2.命题“”的否定是( )
A. B. C. D.
3.已知正实数、满足,则的取值可能为( )
A. B. C. D.
4.已知函数,则函数的图像是( )
A. B. C. D.
5.设为定义上奇函数,当时,(b为常数),则( )
A.3 B. C.-1 D.-3
6.在中,若,则这个三角形的形状是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
7.某地区有20000名考生参加了高三第二次调研考试.经过数据分析,数学成绩X近似服从正态分布,则数学成绩位于[80,88]的人数约为( )
参考数据:,,.
A.455 B.2718 C.6346 D.9545
8.若抛掷两枚骰子出现的点数分别为a,b,则“在函数的定义域为R的条件下,满足函数为偶函数”的概率为( )
A. B. C. D.
二、多选题
9.下列叙述中不正确的是( )
A.若,则“不等式恒成立”的充要条件是“”;
B.若,则“”的充要条件是“”;
C.“”是“方程有一个正根和一个负根”的必要不充分条件;
D.“”是“”的充分不必要条件.
10.给出下列四个命题,其中是真命题的为( )
A.如果θ是第一或第四象限角,那么
B.如果,那么θ是第一或第四象限角
C.终边在x轴上的角的集合为
D.已知扇形OAB的面积为1,周长为4,则扇形的圆心角(正角)的弧度数为2
11.下列说法正确的有( )
A.若事件与事件互斥,则事件与事件对立
B.若随机变量,则方差
C.若随机变量,,则
D.以模型去拟合一组数据时,为了求出回归方程,设,求得线性回归方程为,则的值分别是和
12.乒乓球,被称为中国的“国球”.某次比赛采用五局三胜制,当参赛甲 乙两位中有一位赢得三局比赛时,就由该选手晋级而比赛结束.每局比赛皆须分出胜负,且每局比赛的胜负不受之前比赛结果影响.假设甲在任一局赢球的概率为,实际比赛局数的期望值记为,则下列说法中正确的是( )
A.三局就结束比赛的概率为 B.的常数项为3
C.函数在上单调递减 D.
三、填空题
13.已知函数,则方程的解为________.
14.已知,则__________.
15.已知函数的极小值为2,则______
16.2021年11月27日奥密克戎毒株输入我国香港,某医院委派甲、乙、丙、丁四名医生前往三个小区做好防疫工作,每个小区至少委派一名医生,在甲派往小区的条件下,乙派往小区的概率为____.
四、解答题
17.已知函数.
(1)当时,求值; (2)若是偶函数,求的最大值.
18.设集合,.
(1)若,求;
(2)当时,求实数的取值范围.
19.已知-<x<0,sin x+cos x=.
(1)求sinxcosx; (2)求sinx-cosx的值
20.某校为了丰富学生课余生活,组建了足球社团.为了解学生喜欢足球是否与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
喜欢足球 不喜欢足球 合计
男生 40
女生 30
合计
(1)根据所给数据完成上表,依据的独立性检验,能否认为该校学生喜欢足球与性别有关?
(2)社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知这两名男生进球的概率均为,这名女生进球的概率为,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.
附:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
21.某企业有甲、乙两个研发小组,甲组研究新产品成功的概率为,乙组研究新产品成功的概率为,现安排甲组研发新产品,乙组研发新产品,设甲、乙两组的研发相互独立.
(1)求恰好有一种新产品研发成功的概率;
(2)若新产品研发成功,预计企业可获得利润120万元,不成功则会亏损50万元;若新产品研发成功,企业可获得利润100万元,不成功则会亏损40万元,求该企业获利万元的分布列.
22.已知函数.
(1)若的图象在处的切线与直线垂直,求实数的值;
(2)讨论在上的单调性.
22-23学年下高二期中数学试题(第 4页,共 4 页)
2022-2023学年(下)厦门市五显中学高二年期中试卷数学学科参考答案:
1.D 2.D 3.D 4.C 5.D 6.B
7.B【详解】由题意可知,,
则数学成绩位于[80,88]的人数约为.故选:B
8.B【详解】抛掷两枚骰子出现的点数分别为a,b,共36种情况,如下
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
记函数的定义域为R为事件A,
即恒成立,需满足,即,
满足的有26种情况,故.
记函数为偶函数为事件B,
函数的定义域为,由偶函数的定义知,即或.
满足或的有6种情况,故,
故,故选:B
9.AB 10.AD
11.BCD【详解】由对立事件和互斥事件定义可得,对立事件是互斥的,互斥事件不一定对立,所以A选项错误;
由二项分布可得,又由公式可得
,所以B选项正确;
正态分布,对称轴, ,
得,又因为与关于对称,所以,所以C选项正确;
将两边同时取得,,与对应,
则,即,,所以D选项正确.故选:BCD
12.ABD【详解】设实际比赛局数为,则的可能取值为,
所以,,
,因此三局就结束比赛的概率为,则A正确;
故
, 由知常数项为3,故B正确;
由,故D正确;
由,
,所以,
令,则;令,则,
则函数在上单调递增,则C不正确.故选:ABD.
13.1 14. 15.
16.【详解】记事件为“甲派往小区”,事件为“乙派往小区”,则
若A小区分配甲一个人,则有,若A小区分配甲以及另一个人一起,则有,故事件包含的基本事件个数为,
在甲派往小区的条件下,乙派往小区的情况为:①只有甲派往小区,只有乙派往小区,另外两个人去C小区,则有1种情况,②从丙丁中选一个人连同甲一起派往小区,只有乙派往小区,剩下一个人去C小区,则有种情况,③从丙丁中选一个人连同乙一起派往小区,只有甲派往小区,剩下一个人去C小区,则有种情况,
,故答案为:
17.解:当时,,所以;
(2)因为是偶函数,所以成立,
即成立,
所以,则,所以的最大值为2.
18.【详解】(1)因为,所以集合
集合,所以,
所以
(2)因为,所以,所以,解得.
19.(1)由sin x+cos x=两边平方得,
所以.
(2)因为-<x<0,所以,,
所以
20.【详解】(1)列联表如下:
喜欢足球 不喜欢足球 合计
男生 60 40 100
女生 30 70 100
合计 90 110 200
则,
所以依据的独立性检验,能认为该校学生喜欢足球与性别有关.
(2)依题意得3人进球总次数的所有可能取值为,
,,
,,
所以的分布列如下:
0 1 2 3
所以的数学期望为.
21.(1)因为甲、乙两个研发小组研究新产品成功的概率分别为为和,且相互独立,
所以,恰好有一种新产品研发成功的概率;
(2)根据题意,的可能取值有.
,
所以分布列为:
22.(1)由题知,,,解得.
(2)
(i)当时,若,则,
若,此时开口向下,对称轴为,
所以当时,,
在单调递减;
(ii)当时,开口向上,,
则(根据二次函数大致图象知舍去)
且当时,单调递减;
当时,单调递增.
(iii)当时,开口向上,对称轴在单调递增,
当时,在单调递增.
综上:当时,在单调递减;
当时,在单调递减,在单调递增,
当时,在单调递增.
同课章节目录
