第6单元正比例和反比例必考题检测卷(单元卷) 小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元正比例和反比例必考题检测卷(单元卷) 小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 14:25:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例必考题检测卷(单元卷)-小学数学六年级下册苏教版
一、选择题
1.下面题中的两个相关联的量( )
电脑的单价一定,购置电脑的数量和总价
A.成正比例 B.成反比例 C.不成比例
2.下题中的两种量成什么比例.()
班级人数一定,每行站的人数和站的行数.
A.成正比例 B.成反比例 C.不成比例
3.甲、乙、丙三人赛跑,甲比乙快 ,乙比丙慢 ,甲和丙两人比较( )
A.甲、丙一样快 B.甲快一些 C.丙快一些
4.把36升水倒入一个长方体容器中,水的高度和容器内部的底面积( ).
A.成正比例 B.成反比例 C.不成比例
5.a÷b=c,当c一定时a和b( );当a一定时b和c( );当b一定时a和c( )。
①成正比例 ②成反比例 ③不成比例
A.①②① B.①③① C.①②③
6.用面积是9dm2的方砖,需要96块。如果改用面积是4dm2的方砖,需要( )块。
A.4x=9×96 B.4×4×x=9×9×96 C.96÷9=x÷4
二、填空题
7.长方体的高一定,体积与底面积成( )比例。
8.如果5x=7y(x0),那么x:y=( ):( ),由此可知x和y成( )比例。
9.已知x、y是两种相关联的量,k是个固定的不为0的数。
(1)当=y时,x,y成( )比例。
(2)当=y时,x,y成( )比例。
10.下表中,如果x和y成正比例,那么空格里应填( );如果x和y成反比例,那么空格里应填( )
x 8 12
y 3
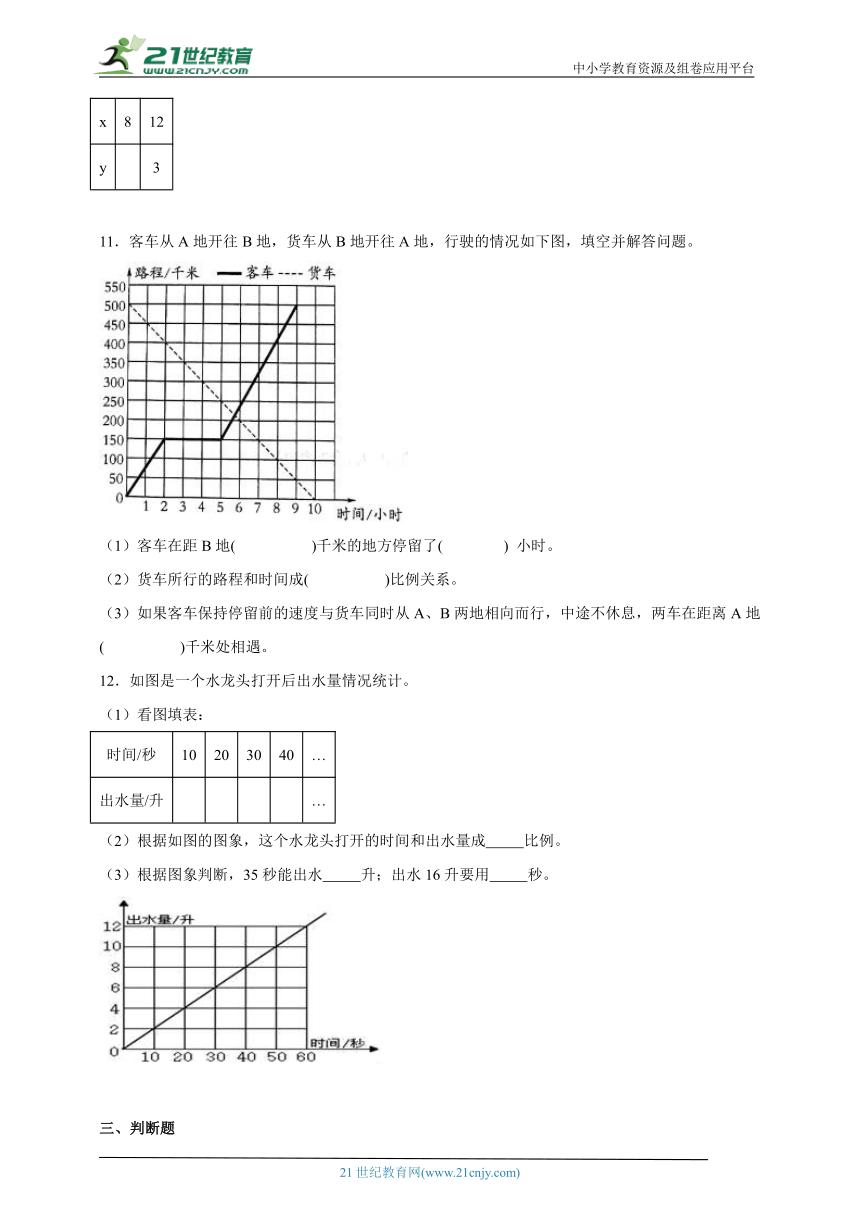
11.客车从A地开往B地,货车从B地开往A地,行驶的情况如下图,填空并解答问题。
(1)客车在距B地( )千米的地方停留了( ) 小时。
(2)货车所行的路程和时间成( )比例关系。
(3)如果客车保持停留前的速度与货车同时从A、B两地相向而行,中途不休息,两车在距离A地( )千米处相遇。
12.如图是一个水龙头打开后出水量情况统计。
(1)看图填表:
时间/秒 10 20 30 40 …
出水量/升 …
(2)根据如图的图象,这个水龙头打开的时间和出水量成 比例。
(3)根据图象判断,35秒能出水 升;出水16升要用 秒。
三、判断题
13.如果x=(y≠0),那么x和y成反比例。( )
14.圆的直径和它的半径成正比例。( )
15.大圆半径是小圆半径的4倍,则小圆面积与大圆面积的比是1∶4。( )
16.如果x和y成正比例,那么当x扩大时,y也随着扩大。( )
17.修建城铁13号线,已经修的长度与没有修的长度成反比例关系。( )
四、计算题
18.解方程。
五、解答题
19.哥哥买一本书花去自己钱数的,妹妹买的两本书花去自己钱数的,他们剩下的钱数同样多,哥哥和妹妹原来钱数的比是多少?
20.一辆汽车从甲城开往乙城,前3小时行驶180km,用同样的速度再行驶2.4小时就到达乙城。甲、乙两城间的路程是多少千米?(用比例知识解答)
21.装订一批图书,如果每天装订1500册,12天可以装订完;如果需要8天装订完,每天应装订多少册?(用比例解,并写出判断过程)
22.在相同时刻的物高与影长成正比例,如果在某时,旗杆在地面上的影长为10米,身高是1.8米的小明的影长是1.5米,旗杆的高度是多少米?
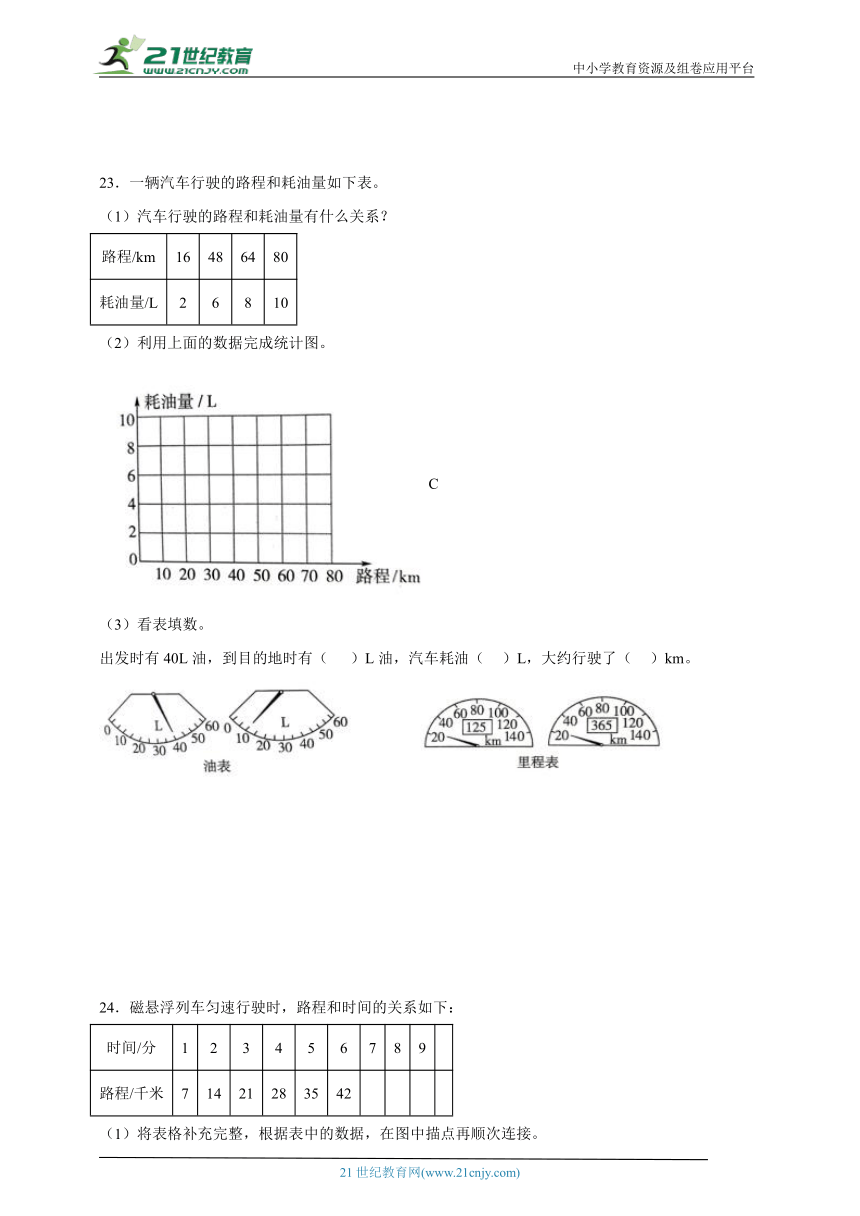
23.一辆汽车行驶的路程和耗油量如下表。
(1)汽车行驶的路程和耗油量有什么关系?
路程/km 16 48 64 80
耗油量/L 2 6 8 10
(2)利用上面的数据完成统计图。
C
(3)看表填数。
出发时有40L油,到目的地时有( )L油,汽车耗油( )L,大约行驶了( )km。
24.磁悬浮列车匀速行驶时,路程和时间的关系如下:
时间/分 1 2 3 4 5 6 7 8 9
路程/千米 7 14 21 28 35 42
(1)将表格补充完整,根据表中的数据,在图中描点再顺次连接。
(2)哪个量没变?路程和时间之间成什么比例?
(3)列车行驶2分半时,所行路程是多少?
参考答案:
1.A
【分析】两种相关联的量,一种量随着另一种量的变化而变化,它们的商一定,它们的关系就是正比例关系.
【详解】单价=总价÷数量,所以电脑的单价一定,购置电脑的数量和总价成正比例.
故选A
2.B
【分析】两种相关联的量,一种量随着另一种量的变化而变化,一种量变大,另一种量变小,它们的积一定,它们的关系就是反比例关系.
【详解】每行站的人数×站的行数=班级人数一定,所以每行站的人数和站的行数成反比例.
故选B
3.C
【分析】根据乙比丙慢, 则把丙的速度看作单位“1”的量,乙的速度用1-表示,再根据甲比乙快, 则把乙的速度看作单位“1”的量,进而求出甲的速度,最后再用丙的速度与甲的速度相比即可.
【详解】丙:“1”,乙:1-=, 甲:×(1+)=
1>, 所以,丙比甲快.
故答案为C.
4.B
【详解】略
5.A
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系。
【详解】a÷b=c:
当c一定时,a和b的比值一定,a和b比值一定成正比例;
当a一定时,因为a÷b=c,所以b×c=a(一定),b和c乘积一定成反比例;
当b一定时,因为a÷b=c,所以a÷c=b(一定),a和c比值一定成正比例。
【点睛】此题重点考查用正比例和反比例的意义来辨识成正比例的量和成反比例的量。
6.A
【详解】因为房间的总面积一定,所需方砖的块数和每块方砖的面积成反比例。显然C不正确,而题目中已知条件是方砖的面积而不是方砖的边长,所以B不正确。
7.正
【详解】略
8. 7 5 正
【分析】看两个相关联的量成什么比例,就看是比值一定还是乘积一定,比值一定成正比例,乘积一定成反比例。
【详解】因为5x=7y,所以x:y=7:5=(一定),所以x和y成正比例。
【点睛】考查了正比例和反比例知识。属于基础题。
9. 正 反
【详解】(1)=k,x,y成正比例。
(2)xy=k,x,y成反比例。
10. 2 4.5
【详解】8∶y=12∶3
解:y=2
8y=12×3
解:y=4.5
11. 350 3 正 300
【分析】(1)根据图示可知,AB两地相距500千米,客车行至距离A地150千米的地方,从出发2小时,休息至出发5小时,所以,客车距离B地距离为:500-150=350(千米),休息时间为:5-2=3(小时);
(2)因为500÷10=50(千米/小时),即路程÷时间=速度(一定),所以所行路程与时间成 正比例关系;
(3)分别求出客货两车的速度,然后利用相遇问题公式:相遇时间=路程和÷速度和,求二人相遇时间,然后求客车所走路程,即距离A点的距离。
【详解】(1)500-150=350(千米)
5-2=3(小时)
(2)500÷10=50(千米/小时)
货车所行路程与时间成正比例关系。
(3)500÷10=50(千米/小时)
150÷2=75(千米/小时)
500÷(75+50)
=500÷125
=4(小时)
4×75=300(千米)
【点睛】本题主要考查复式折线统计图的应用,关键根据统计图找对相关信息,解决问题。
12.(1)
时间/秒 10 20 30 40 …
出水量/升 2 4 6 8 …
(2)正
(3)7;80
【分析】(2)根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量。由此可知,这个水龙头打开的时间和出水量成正比例。
(3)过30秒与40秒中间的点作时间轴的垂线与表示水量的线相交,过这个交点作出水量轴的垂线,垂足处的数值就是35秒的出水量;同样,过出水量轴上表示16升的点作出水量轴的垂线与表示出水量的线相交,过这个交点作时间轴的垂线,垂足处的值就是出水16升的时间。
【详解】(1)由图可以看出,时间为10秒时,出水量为2升、时间为20秒时,出水量为4升、时间为30秒时,出水量为6升、时间为40秒时,出水量为8升……
(2)由统计图(表)可以看出,10:2=5、(20﹣10):(4﹣2)=5、(30﹣20):(6﹣4)=5……时间与出水量的比值是一定的。
(3)如图:
根据图象判断,35秒能出水7升;出水16升要用80秒。
13.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果比值和乘积都不一定,则不成比例。
【详解】因为x=(y≠0),xy=6所以,x和y成反比例。
故此题说法正确。
【点睛】明确x和y之间的乘积是否一定是判断x和y是否成反比例的关键。
14.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果比值和乘积都不一定,则不成比例。
【详解】因为圆的直径等于半径的2倍,圆的直径:圆的半径=2:1,比值一定,所以,此题说法正确。
故答案为:正确
【点睛】通过计算两个量之间的比值和乘积的关系来判断两个量是否成比例、成什么比例是解题的关键。
15.×
【分析】根据圆的面积公式,,可知,当半径扩大4倍,面积将扩大=16倍,据此得解。
【详解】设小圆的半径为,则大圆的半径为,则
小圆面积:
大圆面积:
小圆面积∶大圆面积=1∶16
所以原题判断错误。
【点睛】本题考查了比的知识的灵活运用,掌握圆的面积公式是解题关键。
16.√
【解析】略
17.×
【解析】略
18.x=;x=8;x=4
【分析】利用比例基本性质,比例的外项积等于内项积,先把比例转化成方程,再根据等式的性质解方程,据此解答。
【详解】
解:
x=
x=
解:0.25x=1.6×1.25
x=2÷0.25
x=8
∶x=∶5
解:x=×5
x=
x=4
19.18∶25
【分析】把哥哥和妹妹原来的钱数看作单位“1”,找出两人花去的钱数和剩下钱数的关系,突破口在哥哥和妹妹剩下的钱数一样多,最后用比例解答即可。
【详解】解:设哥哥原来的钱数为x,则剩下的钱数为(1-)x,妹妹的原来钱数为y,则剩下的钱数为(1-)y。
(1-)x=(1-)y
x∶y=(1-)∶(1-)
x∶y=∶
x∶y=(×30)∶(×30)
x∶y=18∶25
答:哥哥和妹妹原来钱数的比是18∶25。
【点睛】解答此题的关键是明确单位“1”的变化和熟练掌握比例的基本性质。
20.324千米
【分析】设甲、乙两城间的路程是x千米,根据路程∶时间=速度(一定),列出正比例算式解答即可。
【详解】解:设甲、乙两城间的路程是x千米。
(x-180)∶2.4=180∶3
3x-540=432
3x=972
3x÷3=972÷3
x=324
答:甲、乙两城间的路程是324千米。
【点睛】本题考查了正比例应用题,关键是找到2.4小时对应的路程。
21.2250册
【分析】根据每天装订册数×天数=总图书列出反比例算式,解答即可。
【详解】因为每天装订册数×天数=总图书(一定)所以每天装订册数与天数成反比例关系。
解:设每天应装订x册。
8x=1500×12
8x÷8=18000÷8
x=2250
答:每天应装订2250册。
【点睛】本题考查了反比例应用题,关键是判断出成什么比例关系。
22.12米
【分析】在同一时刻物高和影长成正比,据此解答。
【详解】解:设旗杆的高度是x米
1.8∶1.5=x∶10
解得x=12
答:旗杆的高度是12米。
【点睛】本题主要考查正比例应用题,计算时要细心。
23.(1)正比例关系;
(2)
(3)10;30;240
【分析】(1)算出前几组数据的商,商一定就是正比例;
(2)根据数据先描点,再连线,画出统计图即可;
(3)看表填空即可。
【详解】(1)16÷2=8(千米),48÷6=8(千米),64÷8=8(千米),路程÷耗油量=一升油行驶路程(一定)
答:汽车行驶的路程和耗油量成正比例关系。
(2)
(3)40-10=30(升)365-125=240(千米)
出发时有40L油,到目的地时有( 10 )L油,汽车耗油( 30 )L,大约行驶了( 240 )km。
【点睛】本题考查了正比例,商一定是正比例,正比例图像是一条经过原点的直线。
24.(1)49;56;63;
(2)由路程÷时间=速度(一定),可知速度没有变,路程与时间成正比例。
(3)17.5千米
【分析】(1)根据统计表,速度是每分钟7千米,根据关系式:速度×时间=路程,由此完成上表,再从而完成统计图即可;
(2)根据路程和时间之间的变化关系得出路程与时间成正比例关系;
(3)根据关系式:速度×时间=路程,代入数据即可;
【详解】(1)49 56 63
(2)由路程÷时间=速度(一定),可知速度没有变,路程与时间成正比例。
(3)2分半=2.5分
7×2.5=17.5(千米)
答:列车行驶2分半时,所行路程是17.5千米。
【点睛】本题主要考查正比例的意义,牢记路程、时间、速度三者的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例必考题检测卷(单元卷)-小学数学六年级下册苏教版
一、选择题
1.下面题中的两个相关联的量( )
电脑的单价一定,购置电脑的数量和总价
A.成正比例 B.成反比例 C.不成比例
2.下题中的两种量成什么比例.()
班级人数一定,每行站的人数和站的行数.
A.成正比例 B.成反比例 C.不成比例
3.甲、乙、丙三人赛跑,甲比乙快 ,乙比丙慢 ,甲和丙两人比较( )
A.甲、丙一样快 B.甲快一些 C.丙快一些
4.把36升水倒入一个长方体容器中,水的高度和容器内部的底面积( ).
A.成正比例 B.成反比例 C.不成比例
5.a÷b=c,当c一定时a和b( );当a一定时b和c( );当b一定时a和c( )。
①成正比例 ②成反比例 ③不成比例
A.①②① B.①③① C.①②③
6.用面积是9dm2的方砖,需要96块。如果改用面积是4dm2的方砖,需要( )块。
A.4x=9×96 B.4×4×x=9×9×96 C.96÷9=x÷4
二、填空题
7.长方体的高一定,体积与底面积成( )比例。
8.如果5x=7y(x0),那么x:y=( ):( ),由此可知x和y成( )比例。
9.已知x、y是两种相关联的量,k是个固定的不为0的数。
(1)当=y时,x,y成( )比例。
(2)当=y时,x,y成( )比例。
10.下表中,如果x和y成正比例,那么空格里应填( );如果x和y成反比例,那么空格里应填( )
x 8 12
y 3
11.客车从A地开往B地,货车从B地开往A地,行驶的情况如下图,填空并解答问题。
(1)客车在距B地( )千米的地方停留了( ) 小时。
(2)货车所行的路程和时间成( )比例关系。
(3)如果客车保持停留前的速度与货车同时从A、B两地相向而行,中途不休息,两车在距离A地( )千米处相遇。
12.如图是一个水龙头打开后出水量情况统计。
(1)看图填表:
时间/秒 10 20 30 40 …
出水量/升 …
(2)根据如图的图象,这个水龙头打开的时间和出水量成 比例。
(3)根据图象判断,35秒能出水 升;出水16升要用 秒。
三、判断题
13.如果x=(y≠0),那么x和y成反比例。( )
14.圆的直径和它的半径成正比例。( )
15.大圆半径是小圆半径的4倍,则小圆面积与大圆面积的比是1∶4。( )
16.如果x和y成正比例,那么当x扩大时,y也随着扩大。( )
17.修建城铁13号线,已经修的长度与没有修的长度成反比例关系。( )
四、计算题
18.解方程。
五、解答题
19.哥哥买一本书花去自己钱数的,妹妹买的两本书花去自己钱数的,他们剩下的钱数同样多,哥哥和妹妹原来钱数的比是多少?
20.一辆汽车从甲城开往乙城,前3小时行驶180km,用同样的速度再行驶2.4小时就到达乙城。甲、乙两城间的路程是多少千米?(用比例知识解答)
21.装订一批图书,如果每天装订1500册,12天可以装订完;如果需要8天装订完,每天应装订多少册?(用比例解,并写出判断过程)
22.在相同时刻的物高与影长成正比例,如果在某时,旗杆在地面上的影长为10米,身高是1.8米的小明的影长是1.5米,旗杆的高度是多少米?
23.一辆汽车行驶的路程和耗油量如下表。
(1)汽车行驶的路程和耗油量有什么关系?
路程/km 16 48 64 80
耗油量/L 2 6 8 10
(2)利用上面的数据完成统计图。
C
(3)看表填数。
出发时有40L油,到目的地时有( )L油,汽车耗油( )L,大约行驶了( )km。
24.磁悬浮列车匀速行驶时,路程和时间的关系如下:
时间/分 1 2 3 4 5 6 7 8 9
路程/千米 7 14 21 28 35 42
(1)将表格补充完整,根据表中的数据,在图中描点再顺次连接。
(2)哪个量没变?路程和时间之间成什么比例?
(3)列车行驶2分半时,所行路程是多少?
参考答案:
1.A
【分析】两种相关联的量,一种量随着另一种量的变化而变化,它们的商一定,它们的关系就是正比例关系.
【详解】单价=总价÷数量,所以电脑的单价一定,购置电脑的数量和总价成正比例.
故选A
2.B
【分析】两种相关联的量,一种量随着另一种量的变化而变化,一种量变大,另一种量变小,它们的积一定,它们的关系就是反比例关系.
【详解】每行站的人数×站的行数=班级人数一定,所以每行站的人数和站的行数成反比例.
故选B
3.C
【分析】根据乙比丙慢, 则把丙的速度看作单位“1”的量,乙的速度用1-表示,再根据甲比乙快, 则把乙的速度看作单位“1”的量,进而求出甲的速度,最后再用丙的速度与甲的速度相比即可.
【详解】丙:“1”,乙:1-=, 甲:×(1+)=
1>, 所以,丙比甲快.
故答案为C.
4.B
【详解】略
5.A
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系。
【详解】a÷b=c:
当c一定时,a和b的比值一定,a和b比值一定成正比例;
当a一定时,因为a÷b=c,所以b×c=a(一定),b和c乘积一定成反比例;
当b一定时,因为a÷b=c,所以a÷c=b(一定),a和c比值一定成正比例。
【点睛】此题重点考查用正比例和反比例的意义来辨识成正比例的量和成反比例的量。
6.A
【详解】因为房间的总面积一定,所需方砖的块数和每块方砖的面积成反比例。显然C不正确,而题目中已知条件是方砖的面积而不是方砖的边长,所以B不正确。
7.正
【详解】略
8. 7 5 正
【分析】看两个相关联的量成什么比例,就看是比值一定还是乘积一定,比值一定成正比例,乘积一定成反比例。
【详解】因为5x=7y,所以x:y=7:5=(一定),所以x和y成正比例。
【点睛】考查了正比例和反比例知识。属于基础题。
9. 正 反
【详解】(1)=k,x,y成正比例。
(2)xy=k,x,y成反比例。
10. 2 4.5
【详解】8∶y=12∶3
解:y=2
8y=12×3
解:y=4.5
11. 350 3 正 300
【分析】(1)根据图示可知,AB两地相距500千米,客车行至距离A地150千米的地方,从出发2小时,休息至出发5小时,所以,客车距离B地距离为:500-150=350(千米),休息时间为:5-2=3(小时);
(2)因为500÷10=50(千米/小时),即路程÷时间=速度(一定),所以所行路程与时间成 正比例关系;
(3)分别求出客货两车的速度,然后利用相遇问题公式:相遇时间=路程和÷速度和,求二人相遇时间,然后求客车所走路程,即距离A点的距离。
【详解】(1)500-150=350(千米)
5-2=3(小时)
(2)500÷10=50(千米/小时)
货车所行路程与时间成正比例关系。
(3)500÷10=50(千米/小时)
150÷2=75(千米/小时)
500÷(75+50)
=500÷125
=4(小时)
4×75=300(千米)
【点睛】本题主要考查复式折线统计图的应用,关键根据统计图找对相关信息,解决问题。
12.(1)
时间/秒 10 20 30 40 …
出水量/升 2 4 6 8 …
(2)正
(3)7;80
【分析】(2)根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量。由此可知,这个水龙头打开的时间和出水量成正比例。
(3)过30秒与40秒中间的点作时间轴的垂线与表示水量的线相交,过这个交点作出水量轴的垂线,垂足处的数值就是35秒的出水量;同样,过出水量轴上表示16升的点作出水量轴的垂线与表示出水量的线相交,过这个交点作时间轴的垂线,垂足处的值就是出水16升的时间。
【详解】(1)由图可以看出,时间为10秒时,出水量为2升、时间为20秒时,出水量为4升、时间为30秒时,出水量为6升、时间为40秒时,出水量为8升……
(2)由统计图(表)可以看出,10:2=5、(20﹣10):(4﹣2)=5、(30﹣20):(6﹣4)=5……时间与出水量的比值是一定的。
(3)如图:
根据图象判断,35秒能出水7升;出水16升要用80秒。
13.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果比值和乘积都不一定,则不成比例。
【详解】因为x=(y≠0),xy=6所以,x和y成反比例。
故此题说法正确。
【点睛】明确x和y之间的乘积是否一定是判断x和y是否成反比例的关键。
14.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果比值和乘积都不一定,则不成比例。
【详解】因为圆的直径等于半径的2倍,圆的直径:圆的半径=2:1,比值一定,所以,此题说法正确。
故答案为:正确
【点睛】通过计算两个量之间的比值和乘积的关系来判断两个量是否成比例、成什么比例是解题的关键。
15.×
【分析】根据圆的面积公式,,可知,当半径扩大4倍,面积将扩大=16倍,据此得解。
【详解】设小圆的半径为,则大圆的半径为,则
小圆面积:
大圆面积:
小圆面积∶大圆面积=1∶16
所以原题判断错误。
【点睛】本题考查了比的知识的灵活运用,掌握圆的面积公式是解题关键。
16.√
【解析】略
17.×
【解析】略
18.x=;x=8;x=4
【分析】利用比例基本性质,比例的外项积等于内项积,先把比例转化成方程,再根据等式的性质解方程,据此解答。
【详解】
解:
x=
x=
解:0.25x=1.6×1.25
x=2÷0.25
x=8
∶x=∶5
解:x=×5
x=
x=4
19.18∶25
【分析】把哥哥和妹妹原来的钱数看作单位“1”,找出两人花去的钱数和剩下钱数的关系,突破口在哥哥和妹妹剩下的钱数一样多,最后用比例解答即可。
【详解】解:设哥哥原来的钱数为x,则剩下的钱数为(1-)x,妹妹的原来钱数为y,则剩下的钱数为(1-)y。
(1-)x=(1-)y
x∶y=(1-)∶(1-)
x∶y=∶
x∶y=(×30)∶(×30)
x∶y=18∶25
答:哥哥和妹妹原来钱数的比是18∶25。
【点睛】解答此题的关键是明确单位“1”的变化和熟练掌握比例的基本性质。
20.324千米
【分析】设甲、乙两城间的路程是x千米,根据路程∶时间=速度(一定),列出正比例算式解答即可。
【详解】解:设甲、乙两城间的路程是x千米。
(x-180)∶2.4=180∶3
3x-540=432
3x=972
3x÷3=972÷3
x=324
答:甲、乙两城间的路程是324千米。
【点睛】本题考查了正比例应用题,关键是找到2.4小时对应的路程。
21.2250册
【分析】根据每天装订册数×天数=总图书列出反比例算式,解答即可。
【详解】因为每天装订册数×天数=总图书(一定)所以每天装订册数与天数成反比例关系。
解:设每天应装订x册。
8x=1500×12
8x÷8=18000÷8
x=2250
答:每天应装订2250册。
【点睛】本题考查了反比例应用题,关键是判断出成什么比例关系。
22.12米
【分析】在同一时刻物高和影长成正比,据此解答。
【详解】解:设旗杆的高度是x米
1.8∶1.5=x∶10
解得x=12
答:旗杆的高度是12米。
【点睛】本题主要考查正比例应用题,计算时要细心。
23.(1)正比例关系;
(2)
(3)10;30;240
【分析】(1)算出前几组数据的商,商一定就是正比例;
(2)根据数据先描点,再连线,画出统计图即可;
(3)看表填空即可。
【详解】(1)16÷2=8(千米),48÷6=8(千米),64÷8=8(千米),路程÷耗油量=一升油行驶路程(一定)
答:汽车行驶的路程和耗油量成正比例关系。
(2)
(3)40-10=30(升)365-125=240(千米)
出发时有40L油,到目的地时有( 10 )L油,汽车耗油( 30 )L,大约行驶了( 240 )km。
【点睛】本题考查了正比例,商一定是正比例,正比例图像是一条经过原点的直线。
24.(1)49;56;63;
(2)由路程÷时间=速度(一定),可知速度没有变,路程与时间成正比例。
(3)17.5千米
【分析】(1)根据统计表,速度是每分钟7千米,根据关系式:速度×时间=路程,由此完成上表,再从而完成统计图即可;
(2)根据路程和时间之间的变化关系得出路程与时间成正比例关系;
(3)根据关系式:速度×时间=路程,代入数据即可;
【详解】(1)49 56 63
(2)由路程÷时间=速度(一定),可知速度没有变,路程与时间成正比例。
(3)2分半=2.5分
7×2.5=17.5(千米)
答:列车行驶2分半时,所行路程是17.5千米。
【点睛】本题主要考查正比例的意义,牢记路程、时间、速度三者的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
