湖南省郴州市永兴县童星学校2022-2023学年高二下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 湖南省郴州市永兴县童星学校2022-2023学年高二下学期期中考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 651.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 10:24:14 | ||
图片预览




文档简介
童星学校2022-2023学年高二下学期期中考试数学试卷
总分:150分 考试时间:120分钟;
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(共40分)
1.、、、四人并排站成一排,如果与相邻,那么不同的排法种数是( )
A.24种 B.12种 C.48种 D.23种
2.设随机变量,,则( )
A. B. C. D.
3.某次考试共有4道单选题,某学生对其中3道题有思路,1道题完全没有思路.有思路的题目每道做对的概率为0.8,没有思路的题目,只好任意猜一个答案,猜对的概率为0.25.若从这4道题中任选2道,则这个学生2道题全做对的概率为( )
A.0.34 B.0.37 C.0.42 D.0.43
4.某地摊集中点在销售旺季的某天接纳顾客量超过1万人次的概率是,连续两天顾客量超过1万人次的概率是,在该地摊集中点在销售旺季的某天接纳顾客量超过1万人次的条件下,随后一天的接纳顾客量超过1万人次概率是( ).
A. B. C. D.
5.下面给出四个随机变量:
①一高速公路上某收费站在半小时内经过的车辆数ξ;
②一个沿直线y=2x进行随机运动的质点,它在该直线上的位置η;
③某指挥台5分钟内接到的雷达电话次数X;
④某同学离开哈尔滨市第三中学的距离Y;
其中是离散型随机变量的为( )
A.①② B.③④ C.①③ D.②④
6.在n次独立重复试验(伯努利试验)中,若每次试验中事件A发生的概率为p,则事件A发生的次数X服从二项分布,事实上,在伯努利试验中,另一个随机变量的实际应用也很广泛,即事件A首次发生时试验进行的次数Y,显然,,2,3,…,我们称Y服从“几何分布”,经计算得.据此,若随机变量X服从二项分布时,且相应的“几何分布”的数学期望,则n的最小值为( )
A.6 B.18 C.36 D.37
7.在如图所示的正方形中随机投掷20000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
附:若X~N(μ,σ2),P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544.
A.4772 B.6826 C.3413 D.9544
8.以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到经验回归方程,则的值分别是( )
A. B. C. D.
二、多选题(共20分)
9.下列命题正确的是( )
附:
0.050 0.01 0.005
3.841 6.635 7.879
A.若甲、乙两组数据的相关系数分别为0.66和,则乙组数据的线性相关性更强
B.已知样本数据的方差为4,则的标准差是4
C.在检验A与B是否有关的过程中,根据所得数据算得,则有99%的把握认为A和B有关
D.对具有线性相关关系的变量x、y,有一组观测数据,其线性回归方程是,且,则实数的值是
10.下列结论中,正确的有( )
A.数据1,2,4,5,6,8,9的第百分之60分位数为5.
B.已知随机变量X服从二项分布,若,则.
C.已知回归直线方程为,且,,则.
D.对变量x与y的统计量来说,值越小,判断“x与y有关系”的把握性越大.
11.下列说法正确的是( )
A.可表示为
B.6个朋友聚会,见面后每两人握手一次,一共握手15次
C.若把英文“”的字母顺序写错,则可能出现的错误共有59种
D.将4名医护人员安排到呼吸、感染两个科室,要求每个科室至少有1人,则共有18种不同的安排方法
12.下列说法错误的是( )
A.若线性相关系数越接近1,则两个变量的线性相关性越弱
B.已知随机变量服从正态分布,则其期望
C.已知随机变量服从正态分布,且,则
D.已知一组数据的方差是3,则数据的标准差是12
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题(共20分)
13.的展开式中含项的系数为30,则实数a的值为___________.
14.已知随机变量服从两点分布,且,设,那么________.
15.已知的对应值如下表所示:
0 2 4 6 8
1 11
若与线性相关,且回归直线方程为,则__________.
16.学校给每位教师随机发了一箱苹果,李老师将其分为两份,第1份占总数的40%,次品率为5%,第2份占总数的60%,次品率为4%.若李老师分份之前随机拿了一个发现是次品后放回,则该苹果被分到第1份中的概率为______.
四、解答题(共70分)
17.随着社会的进步,科技的发展,越来越多的大学本科生希望通过保研或者考研进入更理想的大学进行研究生阶段的学习.某大学为了解准备保研或者考研的本科生每天课余学习时间,随机抽取了400名大学生进行调查,将收集到的学习时间(单位:小时)数据分成5组:,,,,(学习时间均在内),得到如图所示的频率分布直方图.
(1)求m的值,并估计这400名大学生每天课余学习时间的平均值(同一组中的数据用该组区间的中点值为代表);
(2)按分层抽样的方法从学习时间在和组中抽出8人,再从这8人中随机抽取3人,记X表示抽到的3人中学习时间在组中的人数,求X的分布列和数学期望.
18.作为一种益智游戏,中国象棋具有悠久的历史,中国象棋的背后,体现的是博大精深的中华文化.为了推广中国象棋,某地举办了一次地区性的中国象棋比赛,小明作为选手参加.除小明以外的其他参赛选手中,50%是一类棋手,25%是二类棋手,其余的是三类棋手.小明与一、二、三类棋手比赛获胜的概率分别是0.3、0.4和0.5.
(1)从参赛选手中随机选取一位棋手与小明比赛,求小明获胜的概率;
(2)如果小明获胜,求与小明比赛的棋手为一类棋手的概率.
19.(1)星期一上午某教师要上3个班级的课,每班1节.若上午规定限排4节课,且要求3节课不能连排,则这天上午该教师的课程表有几种不同的排法?
(2)某天的课程表要排入政治、语文、数学、外语、劳技、体育6门课,每门课排1节.若第1节不能排体育课,第6节不能排数学课,则共有几种不同排法?
20.2023年春节过后,随着疫情的有效控制,高三学年开始返校复课学习,为了减少学生买餐时聚集排队,学校食堂从复课之日起,每天中午都会提供拉面和盖饭共两种套餐(每人每次只能选择其中一种),经过一段时间的统计分析发现:学生第一天选择套餐的概率为,选择套餐的概率为.如果第一天选择套餐,那么第二天选择套餐的概率为;如果第一天选择套餐,第二天选择套餐的概率为.
(1)求高三一位同学第二天选择套餐的概率;
(2)记高三某班三位同学复课第二天选择套餐的人数为,求的分布列和数学期望.
21.为提高学生的数学应用能力和创造力,学校打算开设“数学建模”选修课,为了解学生对“数学建模”的兴趣度是否与性别有关,学校随机抽取该校30名高中学生进行问卷调查,其中认为感兴趣的人数占70%.
(1)根据所给数据,完成下面的列联表,并根据列联表判断是否有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关?
感兴趣 不感兴趣 合计
男生 12
女生 5
合计 30
(2)若感兴趣的女生中恰有4名是高三学生,现从感兴趣的女生中随机选出3名进行二次访谈,记选出高三女生的人数为X,求X的分布列与数学期望.
附:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
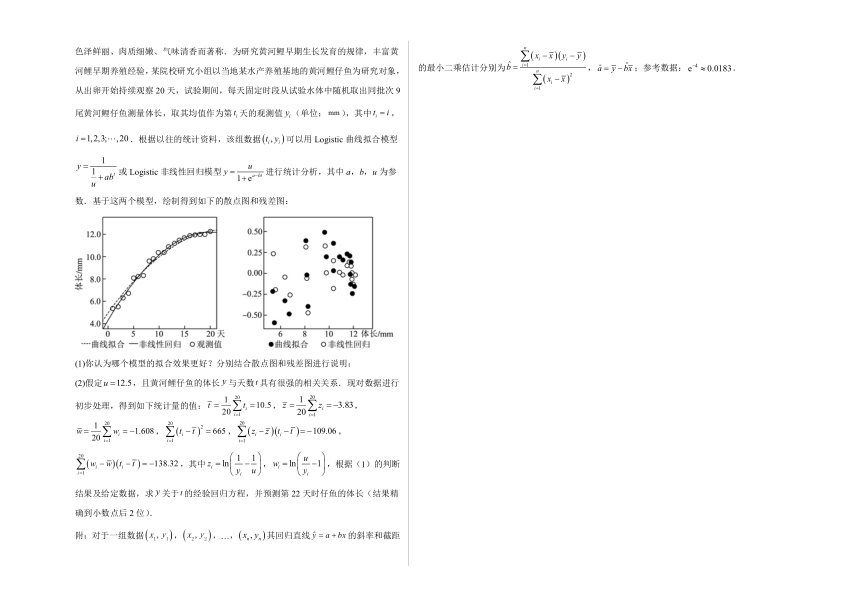
22.黄河鲤是我国华北地区的主要淡水养殖品种之一,其鳞片金黄、体形梭长,尤以色泽鲜丽、肉质细嫩、气味清香而著称.为研究黄河鲤早期生长发育的规律,丰富黄河鲤早期养殖经验,某院校研究小组以当地某水产养殖基地的黄河鲤仔鱼为研究对象,从出卵开始持续观察20天,试验期间,每天固定时段从试验水体中随机取出同批次9尾黄河鲤仔鱼测量体长,取其均值作为第天的观测值(单位:),其中,.根据以往的统计资料,该组数据可以用Logistic曲线拟合模型或Logistic非线性回归模型进行统计分析,其中a,b,u为参数.基于这两个模型,绘制得到如下的散点图和残差图:
(1)你认为哪个模型的拟合效果更好?分别结合散点图和残差图进行说明:
(2)假定,且黄河鲤仔鱼的体长与天数具有很强的相关关系.现对数据进行初步处理,得到如下统计量的值:,,,,,,其中,,根据(1)的判断结果及给定数据,求关于的经验回归方程,并预测第22天时仔鱼的体长(结果精确到小数点后2位).
附:对于一组数据,,…,其回归直线的斜率和截距的最小二乘估计分别为,;参考数据:.
参考答案:
1.B
【分析】利用捆绑法求解相邻问题.
【详解】由题意,因为与相邻,将与放在一起,共有种排法,将与看成一个整体,与、进行全排列,共有种排法,综上共有种排法,
故选:B.
2.C
【分析】利用正态密度曲线的对称性可求得的值,进而可得出的值.
【详解】,,
.
故选:C.
3.C
【分析】根据排列组合以及概率的乘法公式即可求解.
【详解】设事件表示“两道题全做对”,
若两个题目都有思路,则,
若两个题目中一个有思路一个没有思路,则,
故,
故选:C
4.D
【分析】利用条件概率的定义及其概率计算公式求解即可.
【详解】设“某天接纳顾客量超过1万人次”为事件A,“随后一天的接纳顾客量超过1万人次” 为事件B,
则,,
所以,
故选:D.
5.C
【分析】根据给定条件,利用离散型随机变量的定义分析各命题,再判断作答.
【详解】对于①,半小时内经过的车辆数可以一一列举出来,①是离散型随机变量;
对于②,沿直线y=2x进行随机运动的质点,质点在直线上的位置不能一一列举出来,②不是离散型随机变量;
对于③,5分钟内接到的雷达电话次数可以一一列举出来,③是离散型随机变量;
对于④,某同学离开哈尔滨市第三中学的距离可为某一区间内的任意值,不能一一列举出来,④不是离散型随机变量,
所以给定的随机变量是离散型随机变量的有①③.
故选:C
6.D
【分析】根据二项分布和“几何分布”的定义,列不等式求解.
【详解】由题可知,,,,
因为,所以,解得,
所以n的最小值为37.
故选:D.
7.B
【分析】先根据正态分布N(0,1),求出阴影部分面积,再用频率估计概率,即可求出估计值.
【详解】解:由题知曲线C为正态分布N(0,1),
所以,
所以,
所以阴影部分的概率,
设落入阴影部分的点的个数为,
根据频率估计概率,有,
解得:.
故选:B
8.B
【分析】模型两边取对数,又,可得,又已知回归方程,可求的值.
【详解】由题意得,设,可得.
又经验回归方程为,
所以,故.
故选:B
9.ABD
【分析】比较相关系数的绝对值大小即可判断A;根据方差和标准差的关系即可判断B;根据即可判断C;先算出,,再根据其线性回归方程即可求得实数的值,进而即可判断D.
【详解】对于A,由,则乙组数据的线性相关性更强,故A正确;
对于B,由样本数据的方差为4,则的方差是,所以其标准差为4,故B正确;
对于C,由,则没有99%的把握认为A和B有关,故C错误;
对于D,依题意可得,,则,得,故D正确.
故选:ABD.
10.BC
【分析】运用百分位数、二项分布期望及期望运算性质、回归直线必过样本中心、独立性检验的意义依次分析每个选项即可.
【详解】对于A项,,所以第百分之60分位数为6,故A项错误;
对于B项,因为,所以,
所以,解得:,故B项正确;
对于C项,回归直线必过样本中心可得:,解得:,故C项正确;
对于D项,由独立性检验可知,值越大,判断“x与y有关系”的把握性越大,故D项错误.
故选:BC.
11.BC
【分析】根据排列数的计算公式可判断A;两两握手,即随便选出两人握手的所有可能结果数,通过计算即可判断B;先对进行排列,再将放入位置中即可,列出式子计算即可判断C;分3人,1人一组,和2人,2人一组两种情况,分别求出对应的安排方法,相加即可.
【详解】因为,故A错误;
因为6人两两握手,共握(次),故B正确;
先在5个位置中选出3个位置,对进行全排列,剩下两个位置将放入即可,
故有:(种),而正确的共有1种,
所以可能出现的错误共有(种),故C正确;
因为,
当按3,1分组时,先选1人单独一组,剩下3人为一组,
再将两组分配到两个不同科室中:共(种)分法,
当按2,2分组,在4人中选出2人到呼吸科,剩下2人自动去感染科,
故有:(种)分法,故共有(种)安排方法,故D错误.
故选:BC
12.ABD
【分析】根据线性相关系数的概念可判断A,根据正态分布的概念及性质可判断BC,根据方差的性质可判断D.
【详解】对于A,线性相关系数越接近1,则两个变量的线性相关性越强,故A错误;
对于B,因为X服从正态分布,所以,故B错误
对于C,因为服从正态分布,则其正态分布曲线的对称轴为,
所以,
所以,故C正确;
对于D,根据方差的性质可知的方差为,
故所求标准差为,故D错误.
故选:ABD.
13.
【分析】写出的展开式的通项,再令的指数等于和,结合题意即可得解.
【详解】的展开式的通项为,
令,则,令,则(舍去),
所以的展开式中含项的系数为,
所以.
故答案为:.
14.
【解析】先求出,再由随机变量的线性关系的期望性质,即可求解.
【详解】,
故答案为:
【点睛】本题考查两点分布的期望和期望的性质,属于基础题.
15.
【分析】利用回归直线方程经过样本中心点,即可求出结果.
【详解】由表可知,,
因为回归直线方程经过样本中心点,
所以,
解得.
故答案为:2.
16.
【分析】利用贝叶斯公式即可.
【详解】设事件B为“拿的苹果是次品”,为“拿的苹果来自第i份”,
则,,,,
所以,
所求概率为.
故答案为:
17.(1);8.12小时;
(2)分布列见解析,.
【分析】(1)根据各组数据频率之和为1即可求出图中的值,利用平均数计算公式即可求出结果;
(2)根据题意分析的可能取值为0,1,2,3,进而列出分布列求出结果.
【详解】(1)由于各组数据频率之和为1,即,则,
这400名大学生每天课余学习时间的平均值为:
(小时);
(2)由题可知学习时间在和组的频率分别为0.3,0.18,
按分层抽样的方法从学习时间在和组中抽出8人,有5名在内,3名在内,
则的可能取值为0,1,2,3,
则,,
,,
即的分布列为
0 1 2 3
所以.
18.(1)0.375
(2)0.4
【分析】(1)利用条件概率公式求解;
(2)利用条件概率公式求解即可.
【详解】(1)设“小明与第i(,2,3)类棋手相遇”,
根据题意,,
记“小明获胜”,则有,,,
由全概率公式,
小明在比赛中获胜的概率为
,
所以小明获胜的概率为0.375.
(2)小明获胜时,则与小明比赛的棋手为一类棋手的概率为
,
即小明获胜,对手为一类棋手的概率为0.4.
19.(1);(2)504
【分析】(1)直接排列解决减去联排情况.
(2)6节随机排列减去第1节不能排体育课的方法数为和第1节不能排体育课的方法数为再加上体育在第1节,数学在第6节的方法数.
【详解】根据题意为排列所以,三节课联排的方法数为:
所以该教师的课程表有
(2)把政治、语文、数学、外语、劳技、体育6门课随意排到节课的方法数为
第1节排体育课的方法数为,其中包括体育在第1节,数学在第6节的情况
第6节排数学课的方法数为,其中包括体育在第1节,数学在第6节的情况
又因为体育在第1节,数学在第6节的方法数为,所以第1节不能排体育课,第6节不能排数学课的方法数为
20.(1)
(2)分布列见解析,
【分析】(1)利用相互独立与互斥事件的概率计算公式即可得出高三一位同学第二天选择套餐的概率;
(2)由题意可得,进而得出分布列与数学期望.
【详解】(1)由题意可得高三一位同学第二天选择套餐的概率(A);
(2)由题意可得,,1,2,3,
,
可得,,,,
的分布列为:
0 1 2 3
.
21.(1)表格见解析,没有85%的把握;
(2)分布列见解析,.
【分析】(1)由题可得列联表,根据列联表可得进而即得;
(2)由题可得X的取值,然后利用古典概型概率公式求概率,进而可得分布列,再利用期望公式即得.
【详解】(1)列联表如下:
感兴趣 不感兴趣 合计
男生 12 4 16
女生 9 5 14
合计 21 9 30
,
所以没有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关;
(2)由题意可知X的取值可能为0,1,2,3,
则,
,
,
,
故X的分布列为
X 0 1 2 3
P
.
22.(1)拟合效果更好,答案见解析
(2),
【分析】(1)根据散点图,结合两个模型的特征进行判断即可;
(2)根据对数的运算性质,结合题中所给的公式和数据进行求解即可.
【详解】(1)Logistic非线性回归模型拟合效果更好.
从散点图看,散点更均匀地分布在该模型拟合曲线附近;
从残差图看,该模型下的残差更均匀地集中在以残差为0的直线为对称轴的水平带状区域内.
(2)将转化为,
则,所以,
所以.
所以关于的经验回归方程为.
当时,体长.
总分:150分 考试时间:120分钟;
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(共40分)
1.、、、四人并排站成一排,如果与相邻,那么不同的排法种数是( )
A.24种 B.12种 C.48种 D.23种
2.设随机变量,,则( )
A. B. C. D.
3.某次考试共有4道单选题,某学生对其中3道题有思路,1道题完全没有思路.有思路的题目每道做对的概率为0.8,没有思路的题目,只好任意猜一个答案,猜对的概率为0.25.若从这4道题中任选2道,则这个学生2道题全做对的概率为( )
A.0.34 B.0.37 C.0.42 D.0.43
4.某地摊集中点在销售旺季的某天接纳顾客量超过1万人次的概率是,连续两天顾客量超过1万人次的概率是,在该地摊集中点在销售旺季的某天接纳顾客量超过1万人次的条件下,随后一天的接纳顾客量超过1万人次概率是( ).
A. B. C. D.
5.下面给出四个随机变量:
①一高速公路上某收费站在半小时内经过的车辆数ξ;
②一个沿直线y=2x进行随机运动的质点,它在该直线上的位置η;
③某指挥台5分钟内接到的雷达电话次数X;
④某同学离开哈尔滨市第三中学的距离Y;
其中是离散型随机变量的为( )
A.①② B.③④ C.①③ D.②④
6.在n次独立重复试验(伯努利试验)中,若每次试验中事件A发生的概率为p,则事件A发生的次数X服从二项分布,事实上,在伯努利试验中,另一个随机变量的实际应用也很广泛,即事件A首次发生时试验进行的次数Y,显然,,2,3,…,我们称Y服从“几何分布”,经计算得.据此,若随机变量X服从二项分布时,且相应的“几何分布”的数学期望,则n的最小值为( )
A.6 B.18 C.36 D.37
7.在如图所示的正方形中随机投掷20000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
附:若X~N(μ,σ2),P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544.
A.4772 B.6826 C.3413 D.9544
8.以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到经验回归方程,则的值分别是( )
A. B. C. D.
二、多选题(共20分)
9.下列命题正确的是( )
附:
0.050 0.01 0.005
3.841 6.635 7.879
A.若甲、乙两组数据的相关系数分别为0.66和,则乙组数据的线性相关性更强
B.已知样本数据的方差为4,则的标准差是4
C.在检验A与B是否有关的过程中,根据所得数据算得,则有99%的把握认为A和B有关
D.对具有线性相关关系的变量x、y,有一组观测数据,其线性回归方程是,且,则实数的值是
10.下列结论中,正确的有( )
A.数据1,2,4,5,6,8,9的第百分之60分位数为5.
B.已知随机变量X服从二项分布,若,则.
C.已知回归直线方程为,且,,则.
D.对变量x与y的统计量来说,值越小,判断“x与y有关系”的把握性越大.
11.下列说法正确的是( )
A.可表示为
B.6个朋友聚会,见面后每两人握手一次,一共握手15次
C.若把英文“”的字母顺序写错,则可能出现的错误共有59种
D.将4名医护人员安排到呼吸、感染两个科室,要求每个科室至少有1人,则共有18种不同的安排方法
12.下列说法错误的是( )
A.若线性相关系数越接近1,则两个变量的线性相关性越弱
B.已知随机变量服从正态分布,则其期望
C.已知随机变量服从正态分布,且,则
D.已知一组数据的方差是3,则数据的标准差是12
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题(共20分)
13.的展开式中含项的系数为30,则实数a的值为___________.
14.已知随机变量服从两点分布,且,设,那么________.
15.已知的对应值如下表所示:
0 2 4 6 8
1 11
若与线性相关,且回归直线方程为,则__________.
16.学校给每位教师随机发了一箱苹果,李老师将其分为两份,第1份占总数的40%,次品率为5%,第2份占总数的60%,次品率为4%.若李老师分份之前随机拿了一个发现是次品后放回,则该苹果被分到第1份中的概率为______.
四、解答题(共70分)
17.随着社会的进步,科技的发展,越来越多的大学本科生希望通过保研或者考研进入更理想的大学进行研究生阶段的学习.某大学为了解准备保研或者考研的本科生每天课余学习时间,随机抽取了400名大学生进行调查,将收集到的学习时间(单位:小时)数据分成5组:,,,,(学习时间均在内),得到如图所示的频率分布直方图.
(1)求m的值,并估计这400名大学生每天课余学习时间的平均值(同一组中的数据用该组区间的中点值为代表);
(2)按分层抽样的方法从学习时间在和组中抽出8人,再从这8人中随机抽取3人,记X表示抽到的3人中学习时间在组中的人数,求X的分布列和数学期望.
18.作为一种益智游戏,中国象棋具有悠久的历史,中国象棋的背后,体现的是博大精深的中华文化.为了推广中国象棋,某地举办了一次地区性的中国象棋比赛,小明作为选手参加.除小明以外的其他参赛选手中,50%是一类棋手,25%是二类棋手,其余的是三类棋手.小明与一、二、三类棋手比赛获胜的概率分别是0.3、0.4和0.5.
(1)从参赛选手中随机选取一位棋手与小明比赛,求小明获胜的概率;
(2)如果小明获胜,求与小明比赛的棋手为一类棋手的概率.
19.(1)星期一上午某教师要上3个班级的课,每班1节.若上午规定限排4节课,且要求3节课不能连排,则这天上午该教师的课程表有几种不同的排法?
(2)某天的课程表要排入政治、语文、数学、外语、劳技、体育6门课,每门课排1节.若第1节不能排体育课,第6节不能排数学课,则共有几种不同排法?
20.2023年春节过后,随着疫情的有效控制,高三学年开始返校复课学习,为了减少学生买餐时聚集排队,学校食堂从复课之日起,每天中午都会提供拉面和盖饭共两种套餐(每人每次只能选择其中一种),经过一段时间的统计分析发现:学生第一天选择套餐的概率为,选择套餐的概率为.如果第一天选择套餐,那么第二天选择套餐的概率为;如果第一天选择套餐,第二天选择套餐的概率为.
(1)求高三一位同学第二天选择套餐的概率;
(2)记高三某班三位同学复课第二天选择套餐的人数为,求的分布列和数学期望.
21.为提高学生的数学应用能力和创造力,学校打算开设“数学建模”选修课,为了解学生对“数学建模”的兴趣度是否与性别有关,学校随机抽取该校30名高中学生进行问卷调查,其中认为感兴趣的人数占70%.
(1)根据所给数据,完成下面的列联表,并根据列联表判断是否有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关?
感兴趣 不感兴趣 合计
男生 12
女生 5
合计 30
(2)若感兴趣的女生中恰有4名是高三学生,现从感兴趣的女生中随机选出3名进行二次访谈,记选出高三女生的人数为X,求X的分布列与数学期望.
附:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
22.黄河鲤是我国华北地区的主要淡水养殖品种之一,其鳞片金黄、体形梭长,尤以色泽鲜丽、肉质细嫩、气味清香而著称.为研究黄河鲤早期生长发育的规律,丰富黄河鲤早期养殖经验,某院校研究小组以当地某水产养殖基地的黄河鲤仔鱼为研究对象,从出卵开始持续观察20天,试验期间,每天固定时段从试验水体中随机取出同批次9尾黄河鲤仔鱼测量体长,取其均值作为第天的观测值(单位:),其中,.根据以往的统计资料,该组数据可以用Logistic曲线拟合模型或Logistic非线性回归模型进行统计分析,其中a,b,u为参数.基于这两个模型,绘制得到如下的散点图和残差图:
(1)你认为哪个模型的拟合效果更好?分别结合散点图和残差图进行说明:
(2)假定,且黄河鲤仔鱼的体长与天数具有很强的相关关系.现对数据进行初步处理,得到如下统计量的值:,,,,,,其中,,根据(1)的判断结果及给定数据,求关于的经验回归方程,并预测第22天时仔鱼的体长(结果精确到小数点后2位).
附:对于一组数据,,…,其回归直线的斜率和截距的最小二乘估计分别为,;参考数据:.
参考答案:
1.B
【分析】利用捆绑法求解相邻问题.
【详解】由题意,因为与相邻,将与放在一起,共有种排法,将与看成一个整体,与、进行全排列,共有种排法,综上共有种排法,
故选:B.
2.C
【分析】利用正态密度曲线的对称性可求得的值,进而可得出的值.
【详解】,,
.
故选:C.
3.C
【分析】根据排列组合以及概率的乘法公式即可求解.
【详解】设事件表示“两道题全做对”,
若两个题目都有思路,则,
若两个题目中一个有思路一个没有思路,则,
故,
故选:C
4.D
【分析】利用条件概率的定义及其概率计算公式求解即可.
【详解】设“某天接纳顾客量超过1万人次”为事件A,“随后一天的接纳顾客量超过1万人次” 为事件B,
则,,
所以,
故选:D.
5.C
【分析】根据给定条件,利用离散型随机变量的定义分析各命题,再判断作答.
【详解】对于①,半小时内经过的车辆数可以一一列举出来,①是离散型随机变量;
对于②,沿直线y=2x进行随机运动的质点,质点在直线上的位置不能一一列举出来,②不是离散型随机变量;
对于③,5分钟内接到的雷达电话次数可以一一列举出来,③是离散型随机变量;
对于④,某同学离开哈尔滨市第三中学的距离可为某一区间内的任意值,不能一一列举出来,④不是离散型随机变量,
所以给定的随机变量是离散型随机变量的有①③.
故选:C
6.D
【分析】根据二项分布和“几何分布”的定义,列不等式求解.
【详解】由题可知,,,,
因为,所以,解得,
所以n的最小值为37.
故选:D.
7.B
【分析】先根据正态分布N(0,1),求出阴影部分面积,再用频率估计概率,即可求出估计值.
【详解】解:由题知曲线C为正态分布N(0,1),
所以,
所以,
所以阴影部分的概率,
设落入阴影部分的点的个数为,
根据频率估计概率,有,
解得:.
故选:B
8.B
【分析】模型两边取对数,又,可得,又已知回归方程,可求的值.
【详解】由题意得,设,可得.
又经验回归方程为,
所以,故.
故选:B
9.ABD
【分析】比较相关系数的绝对值大小即可判断A;根据方差和标准差的关系即可判断B;根据即可判断C;先算出,,再根据其线性回归方程即可求得实数的值,进而即可判断D.
【详解】对于A,由,则乙组数据的线性相关性更强,故A正确;
对于B,由样本数据的方差为4,则的方差是,所以其标准差为4,故B正确;
对于C,由,则没有99%的把握认为A和B有关,故C错误;
对于D,依题意可得,,则,得,故D正确.
故选:ABD.
10.BC
【分析】运用百分位数、二项分布期望及期望运算性质、回归直线必过样本中心、独立性检验的意义依次分析每个选项即可.
【详解】对于A项,,所以第百分之60分位数为6,故A项错误;
对于B项,因为,所以,
所以,解得:,故B项正确;
对于C项,回归直线必过样本中心可得:,解得:,故C项正确;
对于D项,由独立性检验可知,值越大,判断“x与y有关系”的把握性越大,故D项错误.
故选:BC.
11.BC
【分析】根据排列数的计算公式可判断A;两两握手,即随便选出两人握手的所有可能结果数,通过计算即可判断B;先对进行排列,再将放入位置中即可,列出式子计算即可判断C;分3人,1人一组,和2人,2人一组两种情况,分别求出对应的安排方法,相加即可.
【详解】因为,故A错误;
因为6人两两握手,共握(次),故B正确;
先在5个位置中选出3个位置,对进行全排列,剩下两个位置将放入即可,
故有:(种),而正确的共有1种,
所以可能出现的错误共有(种),故C正确;
因为,
当按3,1分组时,先选1人单独一组,剩下3人为一组,
再将两组分配到两个不同科室中:共(种)分法,
当按2,2分组,在4人中选出2人到呼吸科,剩下2人自动去感染科,
故有:(种)分法,故共有(种)安排方法,故D错误.
故选:BC
12.ABD
【分析】根据线性相关系数的概念可判断A,根据正态分布的概念及性质可判断BC,根据方差的性质可判断D.
【详解】对于A,线性相关系数越接近1,则两个变量的线性相关性越强,故A错误;
对于B,因为X服从正态分布,所以,故B错误
对于C,因为服从正态分布,则其正态分布曲线的对称轴为,
所以,
所以,故C正确;
对于D,根据方差的性质可知的方差为,
故所求标准差为,故D错误.
故选:ABD.
13.
【分析】写出的展开式的通项,再令的指数等于和,结合题意即可得解.
【详解】的展开式的通项为,
令,则,令,则(舍去),
所以的展开式中含项的系数为,
所以.
故答案为:.
14.
【解析】先求出,再由随机变量的线性关系的期望性质,即可求解.
【详解】,
故答案为:
【点睛】本题考查两点分布的期望和期望的性质,属于基础题.
15.
【分析】利用回归直线方程经过样本中心点,即可求出结果.
【详解】由表可知,,
因为回归直线方程经过样本中心点,
所以,
解得.
故答案为:2.
16.
【分析】利用贝叶斯公式即可.
【详解】设事件B为“拿的苹果是次品”,为“拿的苹果来自第i份”,
则,,,,
所以,
所求概率为.
故答案为:
17.(1);8.12小时;
(2)分布列见解析,.
【分析】(1)根据各组数据频率之和为1即可求出图中的值,利用平均数计算公式即可求出结果;
(2)根据题意分析的可能取值为0,1,2,3,进而列出分布列求出结果.
【详解】(1)由于各组数据频率之和为1,即,则,
这400名大学生每天课余学习时间的平均值为:
(小时);
(2)由题可知学习时间在和组的频率分别为0.3,0.18,
按分层抽样的方法从学习时间在和组中抽出8人,有5名在内,3名在内,
则的可能取值为0,1,2,3,
则,,
,,
即的分布列为
0 1 2 3
所以.
18.(1)0.375
(2)0.4
【分析】(1)利用条件概率公式求解;
(2)利用条件概率公式求解即可.
【详解】(1)设“小明与第i(,2,3)类棋手相遇”,
根据题意,,
记“小明获胜”,则有,,,
由全概率公式,
小明在比赛中获胜的概率为
,
所以小明获胜的概率为0.375.
(2)小明获胜时,则与小明比赛的棋手为一类棋手的概率为
,
即小明获胜,对手为一类棋手的概率为0.4.
19.(1);(2)504
【分析】(1)直接排列解决减去联排情况.
(2)6节随机排列减去第1节不能排体育课的方法数为和第1节不能排体育课的方法数为再加上体育在第1节,数学在第6节的方法数.
【详解】根据题意为排列所以,三节课联排的方法数为:
所以该教师的课程表有
(2)把政治、语文、数学、外语、劳技、体育6门课随意排到节课的方法数为
第1节排体育课的方法数为,其中包括体育在第1节,数学在第6节的情况
第6节排数学课的方法数为,其中包括体育在第1节,数学在第6节的情况
又因为体育在第1节,数学在第6节的方法数为,所以第1节不能排体育课,第6节不能排数学课的方法数为
20.(1)
(2)分布列见解析,
【分析】(1)利用相互独立与互斥事件的概率计算公式即可得出高三一位同学第二天选择套餐的概率;
(2)由题意可得,进而得出分布列与数学期望.
【详解】(1)由题意可得高三一位同学第二天选择套餐的概率(A);
(2)由题意可得,,1,2,3,
,
可得,,,,
的分布列为:
0 1 2 3
.
21.(1)表格见解析,没有85%的把握;
(2)分布列见解析,.
【分析】(1)由题可得列联表,根据列联表可得进而即得;
(2)由题可得X的取值,然后利用古典概型概率公式求概率,进而可得分布列,再利用期望公式即得.
【详解】(1)列联表如下:
感兴趣 不感兴趣 合计
男生 12 4 16
女生 9 5 14
合计 21 9 30
,
所以没有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关;
(2)由题意可知X的取值可能为0,1,2,3,
则,
,
,
,
故X的分布列为
X 0 1 2 3
P
.
22.(1)拟合效果更好,答案见解析
(2),
【分析】(1)根据散点图,结合两个模型的特征进行判断即可;
(2)根据对数的运算性质,结合题中所给的公式和数据进行求解即可.
【详解】(1)Logistic非线性回归模型拟合效果更好.
从散点图看,散点更均匀地分布在该模型拟合曲线附近;
从残差图看,该模型下的残差更均匀地集中在以残差为0的直线为对称轴的水平带状区域内.
(2)将转化为,
则,所以,
所以.
所以关于的经验回归方程为.
当时,体长.
同课章节目录
