第6单元正比例和反比例复习巩固卷(单元培优) 小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元正比例和反比例复习巩固卷(单元培优) 小学数学六年级下册苏教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 20:19:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例复习巩固卷(单元培优)-小学数学六年级下册苏教版
一、选择题
1.圆的半径和面积( )。
A.成正比例 B.成反比例 C.不成比例
2.下列式子中,x与y成正比例的是( )
A.y=x+8 B.=x C.x=y
3.如果两个数字比值( ),那么这两个数字成正比例关系。
A.相反 B.一定 C.不确定
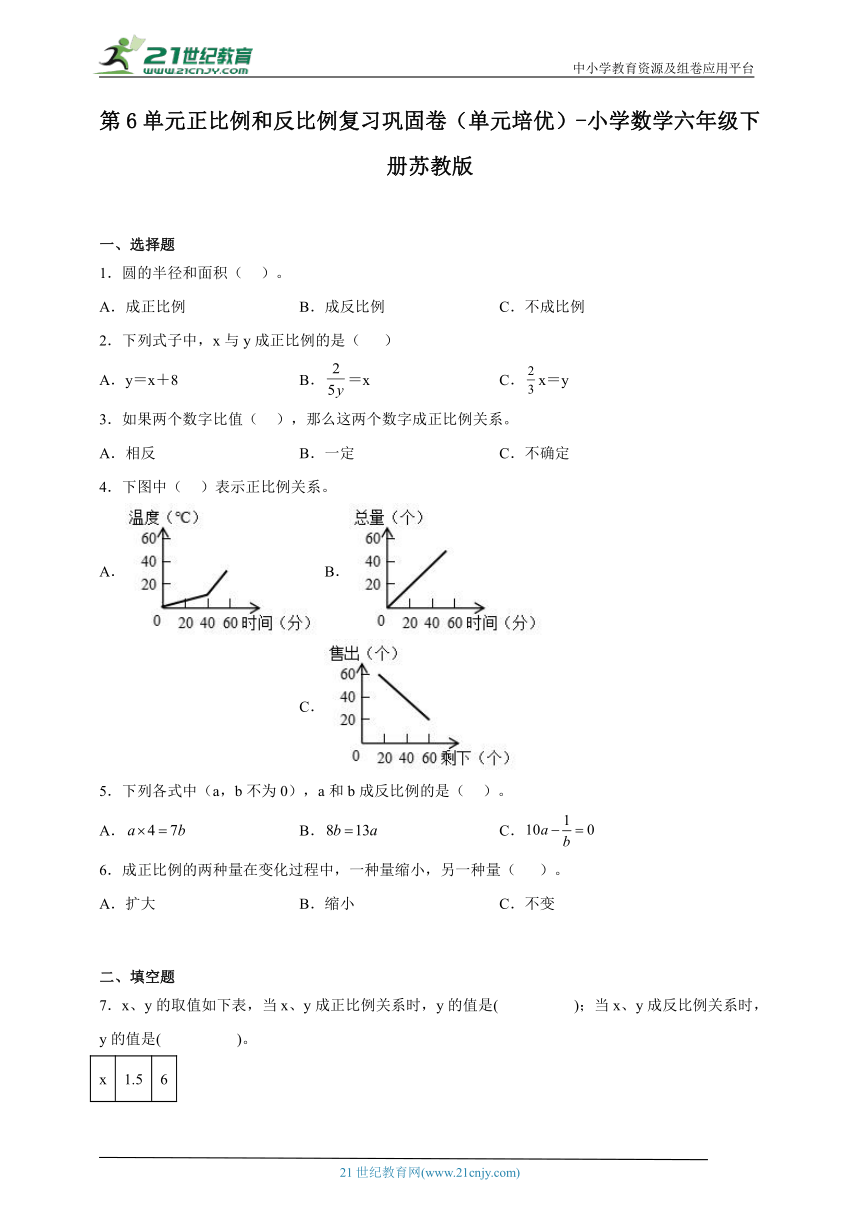
4.下图中( )表示正比例关系。
A.B. C.
5.下列各式中(a,b不为0),a和b成反比例的是( )。
A. B. C.
6.成正比例的两种量在变化过程中,一种量缩小,另一种量( )。
A.扩大 B.缩小 C.不变
二、填空题
7.x、y的取值如下表,当x、y成正比例关系时,y的值是( );当x、y成反比例关系时,y的值是( )。
x 1.5 6
y 2
8.若a∶2=∶b,则a和b成( )比例;若a∶2=b∶,则a和b成( )比例。(a,b均不为0)
9.若a与b成反比例,b与c成反比例,则a与c成( )。
10.运一批砖,每次运的块数与运砖的次数成( )比例;比的后项一定,比的前项与比值成( )比例。
11.下图中,A点表示3小时能做零件( )个,B点表示做360个零件用了( )小时。图中的工作总量和工作时间的( )是一定的,所以工作总量和工作时间成( )比例,这个比值表示( )。
12.一列动车在高速铁路上行驶的时间和路程如下图。看图填写:
(1)这列动车行800千米需要( )小时。
(2)这列动车行驶的时间和路程成( )比例。
(3)照这样计算,4.5小时行驶( )千米。
13.“一台拖拉机2.5小时耕地2.15公顷,照这样计算要耕地6.02公顷,需要多少小时?”此题中( )这个数量是一定的,( )和( )成( )比例。
14.在一幅地图上,1.5cm长的线段表示6km的实际距离,这幅地图的比例尺是( );如果比例尺一定,图上距离和实际距离成( )比例关系。
三、判断题
15.圆锥的体积一定,它的高与底面积成反比例。( )
16.圆周长一定,直径和π成反比例。( )
17.在一定的时间里,做一个零件所用的时间和零件个数成正比例。( )
18.两种相关联的量,不成正比例就成反比例。( )
19.如果3x=5y,那么x∶y=5∶3。( )
四、计算题
20.解比例。
五、解答题
21.一种农药,用药液和水按照2∶500配制而成,5千克药液能配制这种农药多少千克?
22.算一算,想一想。
圆的半径(cm) 1 2 3 4 5
圆的直径(cm)
圆的周长(cm)
圆的面积(cm2)
(1)请把上表补充完整。
(2)从上表中你得到了什么结论 并说明理由。(至少写出两条与正比例和反比例有关的结论)
23.一辆汽车所行的路程和用的时间如下表:
时间/时 1 2 3 4 …
路程/千米 30 60 90 120 …
(1)根据表中的数据,在下图中描出相应的点,并把它们用线连起来。
(2)路程和时间成比例吗?成什么比例?
(3)这辆汽车行驶150千米需要多少小时?
(4)这辆汽车6小时能行多少千米?
24.爸爸打算给亮亮的小书房铺上方砖,用边长2分米的方砖需要90块,如果改用边长3分米的方砖,需要方砖多少块?
25.张大伯想在一个空旷的草场上围出2400平方米的长方形羊圈。请你帮助张大伯在下面表格中列举出几种围法,并计算出每种围法需要栅栏的总长度(接头处不计)。
长/m 120 ……
宽/m 20 ……
栅栏总长度/m 280 ……
(1)根据自己的围法,将表格填写完整。
(2)表格中是否有成正比例或反比例的量?如果有,请完整地表述出来,并说明理由。
26.将一根木料锯成5段要用24分钟,照这样计算,如果要将这根木料锯成8段,要用多少分钟?
参考答案:
1.C
【分析】首先列出圆的面积公式,S圆=πr2,再观察其中半径与面积之间的关系,得出结论。
【详解】S圆=πr2,则(一定)。可知,圆的面积与半径的平方成正比例,与半径不成比例。
故答案为:C。
【点睛】判断两个量是否成正比例、反比例,就看他们的比值一定还是乘积一定,前者成正比例;后者成反比例。
2.C
【详解】x=y
=
故答案为:C
3.B
【详解】这是正比例的定义,也是辨别正比例的方法,同时考察了学生认识和辨别正比例和反比例的能力。
4.B
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。如果用字母和表示两种相关联的量,用表示它们的比值(一定),正比例关系可以用表示,正比例关系的图象是一条从(0,0)出发的直线,据此解答。
【详解】由分析可知,表示正比例关系。
故答案为:B
【点睛】掌握正比例图象的特征是解答题目的关键。
5.C
【分析】根据数量关系判断两个加数的商(比值)一定还是乘积一定,如果商(比值)一定就成正比例,如果乘积一定就成反比例。
【详解】A.因为,所以,a和b成正比例;
B.因为,所以,a和b成正比例;
C.
10ab=1
,成反比例。
故答案为:C
【点睛】此题关键在于懂得正比例和反比例的两个变量数量关系只存在于商和积之间。
6.B
【详解】略
7. 8 0.5
【分析】两个相关联的量,一个量变化,另-一个量也随之变化,它们的比值一定, 这两个量就成正比例,这里x、y成正比例,所以x∶y=1.5∶2,当x=6时,代入比例式即可求出y的值。
两个相关联的量,一个量变化,另一个量也随之变化,它们的积一定,这两个量就成
反比例,这里x、y成反比例,所以xy=1.5×2=3,当x=6时,代入上式即可求出y的值;
由上述计算即可解决问题。
【详解】当x、y成正比例关系时:
x: y=1.5: 2
当x=6时,6∶y=1.5∶2
1.5y=6×2
1.5y=12
y=12÷1.5
y=8
当x、y成反比例关系时:
xy=1.5×2
当x=6时,6y=1.5×2
6y=3
y=3÷6
y=0.5
【点睛】掌握正反比例的概念是解答本题的关键。
8. 反 正
【分析】根据比例的基本性质将比例转化为未知数相乘或相比的形式,再根据正、反比例的意义进行辨识即可。
【详解】若a∶2=∶b,则ab=2×=(乘积一定),所以若a∶2=∶b,则a和b成反比例;
若a∶2=b∶,则a∶b=2∶=10(比值一定),所以若a∶2=b∶,则a和b成正比例。
【点睛】本题主要考查正、反比例的辨识及比例的基本性质的灵活应用。
9.正比例
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为a与b成反比例,所以ab=k1(一定),则b=
因为b与c成反比例,所以bc=k2(一定)
把b=,代入式子bc=k2(一定)
得出:a∶c=(一定)
是a和c对应的比值一定,所以a和c成正比例
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
10. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)每次运的块数×运砖次数=这批砖的总块数(一定),乘积一定,成反比例;
(2)比的前项÷比值=比的后项(一定),比值一定,成正比例。
故答案:(1)反;(2)正。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
11. 180 6 比值 正 每小时做60个零件
【详解】由图可知,A点表示3小时能做零件( 180 )个,B点表示做360个零件用了( 6 )小时。图中的工作总量和工作时间的( 比值 )是一定的,所以工作总量和工作时间成( 正 )比例,这个比值表示( 每小时做60个零件 )。
12. 4 正 900
【详解】略
13. 拖拉机的工作效率 耕地的总量 拖拉机的工作时间 正
【分析】此题中“照这样计算要耕地6.02公顷,需要多少小时?”说明拖拉机工作效率始终不变,拖拉机工作时间会根据耕地总量的变化而变化,因为拖拉机工作效率=,所以根据正比例的含义,拖拉机工作时间和耕地总量相关联,且两者的比值一定,说明这两者成正比例关系
【详解】拖拉机的工作效率这个数量是一定的,耕地的总量和拖拉机的工作时间成正比。
【点睛】掌握判断两种数量是否成正比的方法:首先看这两个量是不是相关联的量,再看比值是否一定。如果相关联且比值一定,则这两种量就成正比例关系。
14. 1∶400000 正
【分析】根据图上距离∶实际距离=比例尺,解答此题即可。
【详解】6千米=600000厘米
1.5∶600000=
即这幅地图的比例尺是,如果比例尺一定,图上距离和实际距离成正比例关系。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
15.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】圆锥的高×底面积=3×圆锥的体积(一定),乘积一定,所以圆锥的高与底面积成反比例。
所以原题说法正确。
故答案为:√。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
16.×
【分析】圆周长=直径×π,两个相关联的量,一种量变化,另一种量也随着变化,这两个量才可能成比例,在圆周长一定的情况下,直径与π这两个量中的π本身就是定值,那么直径也就是定值,这两个量不可能一个变,另一个也变。所以这两个量根本不成反比例。
【详解】根据分析可知,圆周长一定,直径和π不成反比例。
故答案为:×
【点睛】此题主要考查学生对反比例判定的认识与理解。
17.×
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。据此判断。
【详解】在一定的时间里,零件个数×做一个零件所用的时间=工作时间(一定),即零件个数和做一个零件所用的时间,乘积一定,成反比例。
故答案:×
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
18.×
【分析】相关联的两个量,如果它们的比值一定,那么他们成正比例;如果它们的积一定,那么它们成反比例。如果两个量的和一定或者差一定等,它们是不成比例的。
【详解】两种相关联的量,要么成正比例或者成反比例,也可能不成比例。
故答案为:×
【点睛】本题考查相关联的两个量之间的比例关系,注意相关联的两个量,只有积一定或者比值一定时,才会成比例关系。
19.√
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】根据题意可知,x和3为外项,y和5为内项,那么x∶y=5∶3。
故答案为:√
【点睛】应用比例的基本性质是解答此题的关键。
20.x=0.4;x=;x=
x=4.2;x=2;x=36
【分析】根据比例的基本性质将比例转化为方程,再根据等式的性质解方程即可。
【详解】
解:75x=1.2×25
75x=30
x=30÷75
x=0.4
解:54x=3×36
54x=108
x=108÷54
x=2
解:
x=
解:0.4x=0.7×2.4
0.4x=1.68
x=1.68÷0.4
x=4.2
解:54x=36×3
54x=108
x=108÷54
x=2
解:
x=36
【点睛】本题考查了学生根据比例的基本性质和等式的性质解方程的能力,注意等号对齐。
21.1255千克
【分析】把这种比例的农药总量看作单位1,则其中药液的量占总量的,药液的量已知,从而可以用已知一个数的几分之几是多少,求这个数,用除法计算的方法即可求解。
【详解】5÷
=5÷
=1255(千克)
答:5千克药液能配制这种农药1255千克。
【点睛】解答此题的关键是先求出药液占农药总量的分率,进而用除法计算即可求出农药的总量。
22.(1)
圆的半径(cm) 1 2 3 4 5
圆的直径(cm) 2 4 6 8 10
圆的周长(cm) 6.28 12.56 18.84 25.12 31.4
圆的面积(cm2) 3.14 12.56 28.26 50.24 78.5
(2)圆的周长和直径成正比例,圆的面积和半径不成比例等(答案不唯一)
【解析】略
23.(1)如下图:
(2)成比例;成正比例;
(3)5小时
(4)180千米
【分析】(1)根据统计表中的数据描出各点,然后将各点进行连接即可;
(2)根据对应的相关联的量的比值一定就是正比例,故对应的相关联的量的乘积一定就成反比例进行解答;
(3)根据“时间=路程÷速度”代数进行解答;
(4)根据“路程=时间×速度”代数进行解答;
【详解】(1)如下图:
(2)30÷1=60÷2=90÷3=120÷4=30,因此,路程与时间的比值(速度)一定,所以路程和时间成正比例;
(3)150÷30=5(小时)
答:这辆汽车行驶150千米需要5小时。
(4)30×6=180(千米)
答:这辆汽车6小时能行180千米。
【点睛】此题是统计图与行程问题相结合,考查了学生综合运用知识解决问题的能力。
24.40块
【分析】解答此题时应先想书房的面积一定,也就是每块的面积和块数的乘积是一定的,即一块方砖的面积与方砖的块数成反比例,根据已知条件列方程解答即可。
【详解】解:设需要方砖x块。
3×3×x=2×2×90
9x=360
x=40
答:需要方砖40块。
【点睛】解决此题关键是判断出一块方砖的面积与方砖的块数成反比例,注意3分米和2分米都是方砖的边长,而不是方砖的面积。
25.(1)见详解
(2)长方形的长和宽成反比例。因为:120×20=2400(平方米),80×30=2400(平方米),60×40=2400(平方米)。长×宽=长方形的面积(一定),长方形的面积一定,即长和宽的积一定,则长和宽成反比例。
【分析】(1)长方形的面积=长×宽。2400=60×40=80×30。长方形的周长=(长+宽)×2,当长60米,宽40米时,栅栏总长度=(60+40)×2=200(米);当长80米,宽30米时,栅栏总长度=(80+30)×2=220(米)。据此填表。(答案不唯一)
(2)两种相关联的量,它们的商一定,则成正比例;它们的积一定,则成反比例。
【详解】(1)
长/m 120 80 60 ……
宽/m 20 30 40 ……
栅栏总长度/m 280 220 200 ……
(2)长方形的长和宽成反比例。因为:120×20=2400(平方米),80×30=2400(平方米),60×40=2400(平方米)。长×宽=长方形的面积(一定),长方形的面积一定,即长和宽的积一定,则长和宽成反比例。
【点睛】本题考查长方形的周长、面积和反比例的综合应用。根据长方形的面积公式确定长和宽,继而求出周长;根据反比例的意义确定长方形的长和宽成反比例。
26.42分
【分析】想一想,把一根木料锯成5段,要锯几次,锯成8段要锯几次,注意所锯木料的段数比锯的次数要多1,分析题意,根据每锯一次木料所用的时间一定可知,锯的次数与所用时间成正比,设要用x分钟,结合上述提示列出比例式进行求解,即可使问题得解。
【详解】解:设要用x分钟。
x=42
答:要用42分钟。
【点睛】本题考查了植树问题,牢记锯木料的段数比锯的次数要多1,然后找出等量关系,列出比例式,解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例复习巩固卷(单元培优)-小学数学六年级下册苏教版
一、选择题
1.圆的半径和面积( )。
A.成正比例 B.成反比例 C.不成比例
2.下列式子中,x与y成正比例的是( )
A.y=x+8 B.=x C.x=y
3.如果两个数字比值( ),那么这两个数字成正比例关系。
A.相反 B.一定 C.不确定
4.下图中( )表示正比例关系。
A.B. C.
5.下列各式中(a,b不为0),a和b成反比例的是( )。
A. B. C.
6.成正比例的两种量在变化过程中,一种量缩小,另一种量( )。
A.扩大 B.缩小 C.不变
二、填空题
7.x、y的取值如下表,当x、y成正比例关系时,y的值是( );当x、y成反比例关系时,y的值是( )。
x 1.5 6
y 2
8.若a∶2=∶b,则a和b成( )比例;若a∶2=b∶,则a和b成( )比例。(a,b均不为0)
9.若a与b成反比例,b与c成反比例,则a与c成( )。
10.运一批砖,每次运的块数与运砖的次数成( )比例;比的后项一定,比的前项与比值成( )比例。
11.下图中,A点表示3小时能做零件( )个,B点表示做360个零件用了( )小时。图中的工作总量和工作时间的( )是一定的,所以工作总量和工作时间成( )比例,这个比值表示( )。
12.一列动车在高速铁路上行驶的时间和路程如下图。看图填写:
(1)这列动车行800千米需要( )小时。
(2)这列动车行驶的时间和路程成( )比例。
(3)照这样计算,4.5小时行驶( )千米。
13.“一台拖拉机2.5小时耕地2.15公顷,照这样计算要耕地6.02公顷,需要多少小时?”此题中( )这个数量是一定的,( )和( )成( )比例。
14.在一幅地图上,1.5cm长的线段表示6km的实际距离,这幅地图的比例尺是( );如果比例尺一定,图上距离和实际距离成( )比例关系。
三、判断题
15.圆锥的体积一定,它的高与底面积成反比例。( )
16.圆周长一定,直径和π成反比例。( )
17.在一定的时间里,做一个零件所用的时间和零件个数成正比例。( )
18.两种相关联的量,不成正比例就成反比例。( )
19.如果3x=5y,那么x∶y=5∶3。( )
四、计算题
20.解比例。
五、解答题
21.一种农药,用药液和水按照2∶500配制而成,5千克药液能配制这种农药多少千克?
22.算一算,想一想。
圆的半径(cm) 1 2 3 4 5
圆的直径(cm)
圆的周长(cm)
圆的面积(cm2)
(1)请把上表补充完整。
(2)从上表中你得到了什么结论 并说明理由。(至少写出两条与正比例和反比例有关的结论)
23.一辆汽车所行的路程和用的时间如下表:
时间/时 1 2 3 4 …
路程/千米 30 60 90 120 …
(1)根据表中的数据,在下图中描出相应的点,并把它们用线连起来。
(2)路程和时间成比例吗?成什么比例?
(3)这辆汽车行驶150千米需要多少小时?
(4)这辆汽车6小时能行多少千米?
24.爸爸打算给亮亮的小书房铺上方砖,用边长2分米的方砖需要90块,如果改用边长3分米的方砖,需要方砖多少块?
25.张大伯想在一个空旷的草场上围出2400平方米的长方形羊圈。请你帮助张大伯在下面表格中列举出几种围法,并计算出每种围法需要栅栏的总长度(接头处不计)。
长/m 120 ……
宽/m 20 ……
栅栏总长度/m 280 ……
(1)根据自己的围法,将表格填写完整。
(2)表格中是否有成正比例或反比例的量?如果有,请完整地表述出来,并说明理由。
26.将一根木料锯成5段要用24分钟,照这样计算,如果要将这根木料锯成8段,要用多少分钟?
参考答案:
1.C
【分析】首先列出圆的面积公式,S圆=πr2,再观察其中半径与面积之间的关系,得出结论。
【详解】S圆=πr2,则(一定)。可知,圆的面积与半径的平方成正比例,与半径不成比例。
故答案为:C。
【点睛】判断两个量是否成正比例、反比例,就看他们的比值一定还是乘积一定,前者成正比例;后者成反比例。
2.C
【详解】x=y
=
故答案为:C
3.B
【详解】这是正比例的定义,也是辨别正比例的方法,同时考察了学生认识和辨别正比例和反比例的能力。
4.B
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。如果用字母和表示两种相关联的量,用表示它们的比值(一定),正比例关系可以用表示,正比例关系的图象是一条从(0,0)出发的直线,据此解答。
【详解】由分析可知,表示正比例关系。
故答案为:B
【点睛】掌握正比例图象的特征是解答题目的关键。
5.C
【分析】根据数量关系判断两个加数的商(比值)一定还是乘积一定,如果商(比值)一定就成正比例,如果乘积一定就成反比例。
【详解】A.因为,所以,a和b成正比例;
B.因为,所以,a和b成正比例;
C.
10ab=1
,成反比例。
故答案为:C
【点睛】此题关键在于懂得正比例和反比例的两个变量数量关系只存在于商和积之间。
6.B
【详解】略
7. 8 0.5
【分析】两个相关联的量,一个量变化,另-一个量也随之变化,它们的比值一定, 这两个量就成正比例,这里x、y成正比例,所以x∶y=1.5∶2,当x=6时,代入比例式即可求出y的值。
两个相关联的量,一个量变化,另一个量也随之变化,它们的积一定,这两个量就成
反比例,这里x、y成反比例,所以xy=1.5×2=3,当x=6时,代入上式即可求出y的值;
由上述计算即可解决问题。
【详解】当x、y成正比例关系时:
x: y=1.5: 2
当x=6时,6∶y=1.5∶2
1.5y=6×2
1.5y=12
y=12÷1.5
y=8
当x、y成反比例关系时:
xy=1.5×2
当x=6时,6y=1.5×2
6y=3
y=3÷6
y=0.5
【点睛】掌握正反比例的概念是解答本题的关键。
8. 反 正
【分析】根据比例的基本性质将比例转化为未知数相乘或相比的形式,再根据正、反比例的意义进行辨识即可。
【详解】若a∶2=∶b,则ab=2×=(乘积一定),所以若a∶2=∶b,则a和b成反比例;
若a∶2=b∶,则a∶b=2∶=10(比值一定),所以若a∶2=b∶,则a和b成正比例。
【点睛】本题主要考查正、反比例的辨识及比例的基本性质的灵活应用。
9.正比例
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为a与b成反比例,所以ab=k1(一定),则b=
因为b与c成反比例,所以bc=k2(一定)
把b=,代入式子bc=k2(一定)
得出:a∶c=(一定)
是a和c对应的比值一定,所以a和c成正比例
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
10. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)每次运的块数×运砖次数=这批砖的总块数(一定),乘积一定,成反比例;
(2)比的前项÷比值=比的后项(一定),比值一定,成正比例。
故答案:(1)反;(2)正。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
11. 180 6 比值 正 每小时做60个零件
【详解】由图可知,A点表示3小时能做零件( 180 )个,B点表示做360个零件用了( 6 )小时。图中的工作总量和工作时间的( 比值 )是一定的,所以工作总量和工作时间成( 正 )比例,这个比值表示( 每小时做60个零件 )。
12. 4 正 900
【详解】略
13. 拖拉机的工作效率 耕地的总量 拖拉机的工作时间 正
【分析】此题中“照这样计算要耕地6.02公顷,需要多少小时?”说明拖拉机工作效率始终不变,拖拉机工作时间会根据耕地总量的变化而变化,因为拖拉机工作效率=,所以根据正比例的含义,拖拉机工作时间和耕地总量相关联,且两者的比值一定,说明这两者成正比例关系
【详解】拖拉机的工作效率这个数量是一定的,耕地的总量和拖拉机的工作时间成正比。
【点睛】掌握判断两种数量是否成正比的方法:首先看这两个量是不是相关联的量,再看比值是否一定。如果相关联且比值一定,则这两种量就成正比例关系。
14. 1∶400000 正
【分析】根据图上距离∶实际距离=比例尺,解答此题即可。
【详解】6千米=600000厘米
1.5∶600000=
即这幅地图的比例尺是,如果比例尺一定,图上距离和实际距离成正比例关系。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
15.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】圆锥的高×底面积=3×圆锥的体积(一定),乘积一定,所以圆锥的高与底面积成反比例。
所以原题说法正确。
故答案为:√。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
16.×
【分析】圆周长=直径×π,两个相关联的量,一种量变化,另一种量也随着变化,这两个量才可能成比例,在圆周长一定的情况下,直径与π这两个量中的π本身就是定值,那么直径也就是定值,这两个量不可能一个变,另一个也变。所以这两个量根本不成反比例。
【详解】根据分析可知,圆周长一定,直径和π不成反比例。
故答案为:×
【点睛】此题主要考查学生对反比例判定的认识与理解。
17.×
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。据此判断。
【详解】在一定的时间里,零件个数×做一个零件所用的时间=工作时间(一定),即零件个数和做一个零件所用的时间,乘积一定,成反比例。
故答案:×
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
18.×
【分析】相关联的两个量,如果它们的比值一定,那么他们成正比例;如果它们的积一定,那么它们成反比例。如果两个量的和一定或者差一定等,它们是不成比例的。
【详解】两种相关联的量,要么成正比例或者成反比例,也可能不成比例。
故答案为:×
【点睛】本题考查相关联的两个量之间的比例关系,注意相关联的两个量,只有积一定或者比值一定时,才会成比例关系。
19.√
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】根据题意可知,x和3为外项,y和5为内项,那么x∶y=5∶3。
故答案为:√
【点睛】应用比例的基本性质是解答此题的关键。
20.x=0.4;x=;x=
x=4.2;x=2;x=36
【分析】根据比例的基本性质将比例转化为方程,再根据等式的性质解方程即可。
【详解】
解:75x=1.2×25
75x=30
x=30÷75
x=0.4
解:54x=3×36
54x=108
x=108÷54
x=2
解:
x=
解:0.4x=0.7×2.4
0.4x=1.68
x=1.68÷0.4
x=4.2
解:54x=36×3
54x=108
x=108÷54
x=2
解:
x=36
【点睛】本题考查了学生根据比例的基本性质和等式的性质解方程的能力,注意等号对齐。
21.1255千克
【分析】把这种比例的农药总量看作单位1,则其中药液的量占总量的,药液的量已知,从而可以用已知一个数的几分之几是多少,求这个数,用除法计算的方法即可求解。
【详解】5÷
=5÷
=1255(千克)
答:5千克药液能配制这种农药1255千克。
【点睛】解答此题的关键是先求出药液占农药总量的分率,进而用除法计算即可求出农药的总量。
22.(1)
圆的半径(cm) 1 2 3 4 5
圆的直径(cm) 2 4 6 8 10
圆的周长(cm) 6.28 12.56 18.84 25.12 31.4
圆的面积(cm2) 3.14 12.56 28.26 50.24 78.5
(2)圆的周长和直径成正比例,圆的面积和半径不成比例等(答案不唯一)
【解析】略
23.(1)如下图:
(2)成比例;成正比例;
(3)5小时
(4)180千米
【分析】(1)根据统计表中的数据描出各点,然后将各点进行连接即可;
(2)根据对应的相关联的量的比值一定就是正比例,故对应的相关联的量的乘积一定就成反比例进行解答;
(3)根据“时间=路程÷速度”代数进行解答;
(4)根据“路程=时间×速度”代数进行解答;
【详解】(1)如下图:
(2)30÷1=60÷2=90÷3=120÷4=30,因此,路程与时间的比值(速度)一定,所以路程和时间成正比例;
(3)150÷30=5(小时)
答:这辆汽车行驶150千米需要5小时。
(4)30×6=180(千米)
答:这辆汽车6小时能行180千米。
【点睛】此题是统计图与行程问题相结合,考查了学生综合运用知识解决问题的能力。
24.40块
【分析】解答此题时应先想书房的面积一定,也就是每块的面积和块数的乘积是一定的,即一块方砖的面积与方砖的块数成反比例,根据已知条件列方程解答即可。
【详解】解:设需要方砖x块。
3×3×x=2×2×90
9x=360
x=40
答:需要方砖40块。
【点睛】解决此题关键是判断出一块方砖的面积与方砖的块数成反比例,注意3分米和2分米都是方砖的边长,而不是方砖的面积。
25.(1)见详解
(2)长方形的长和宽成反比例。因为:120×20=2400(平方米),80×30=2400(平方米),60×40=2400(平方米)。长×宽=长方形的面积(一定),长方形的面积一定,即长和宽的积一定,则长和宽成反比例。
【分析】(1)长方形的面积=长×宽。2400=60×40=80×30。长方形的周长=(长+宽)×2,当长60米,宽40米时,栅栏总长度=(60+40)×2=200(米);当长80米,宽30米时,栅栏总长度=(80+30)×2=220(米)。据此填表。(答案不唯一)
(2)两种相关联的量,它们的商一定,则成正比例;它们的积一定,则成反比例。
【详解】(1)
长/m 120 80 60 ……
宽/m 20 30 40 ……
栅栏总长度/m 280 220 200 ……
(2)长方形的长和宽成反比例。因为:120×20=2400(平方米),80×30=2400(平方米),60×40=2400(平方米)。长×宽=长方形的面积(一定),长方形的面积一定,即长和宽的积一定,则长和宽成反比例。
【点睛】本题考查长方形的周长、面积和反比例的综合应用。根据长方形的面积公式确定长和宽,继而求出周长;根据反比例的意义确定长方形的长和宽成反比例。
26.42分
【分析】想一想,把一根木料锯成5段,要锯几次,锯成8段要锯几次,注意所锯木料的段数比锯的次数要多1,分析题意,根据每锯一次木料所用的时间一定可知,锯的次数与所用时间成正比,设要用x分钟,结合上述提示列出比例式进行求解,即可使问题得解。
【详解】解:设要用x分钟。
x=42
答:要用42分钟。
【点睛】本题考查了植树问题,牢记锯木料的段数比锯的次数要多1,然后找出等量关系,列出比例式,解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
