19.2.3 一次函数与方程、不等式(3) 课件(共33张PPT)
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式(3) 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 14:37:04 | ||
图片预览










文档简介
(共33张PPT)
19.2.3 一次函数与方程、不等式(3)
人教版八年级下册
知识回顾
1.根据函数 y=2x-1 的图象,利用图象求:
(1)方程 2x-1=0 的解;
(2)不等式 2x-1<0 的解集;
y
x
O
y=2x-1
A
B
1
1
-1
(1)由图象可知,直线y=2x-1与x轴的交点为A(,0),所以方程2x-1=0的解是图象与x轴的交点的横坐标,即x=.
知识回顾
1.根据函数 y=2x-1 的图象,利用图象求:
(1)方程 2x-1=0 的解;
(2)不等式 2x-1<0 的解集;
y
x
O
y=2x-1
A
B
1
1
-1
(2)不等式2x-1<0的解集是函数y=2x-1的图象在x轴下方区域对应的x的取值范围,即x<.
教学目标
1.理解一次函数与二元一次方程(组)的关系.
2.会根据一次函数图象求解二元一次方程(组).
新知导入
二元一次方程 x+y=3 的解有
x=1
y=2
x=-1
y=4
x=0
y=3
x=3
y=0
一次函数 y=-x+3 的图象为:
y
x
O
3
3
y=-x+3
思考:以方程组的解为坐标的点与一次函数的图象有什么关系?
新知小结
从以上例子可以看出:以二元一次方程的解作为点的坐标都在相应的函数图象上;反之,一次函数图象上的点的坐标是对应的二元一次方程的解.
新知探究
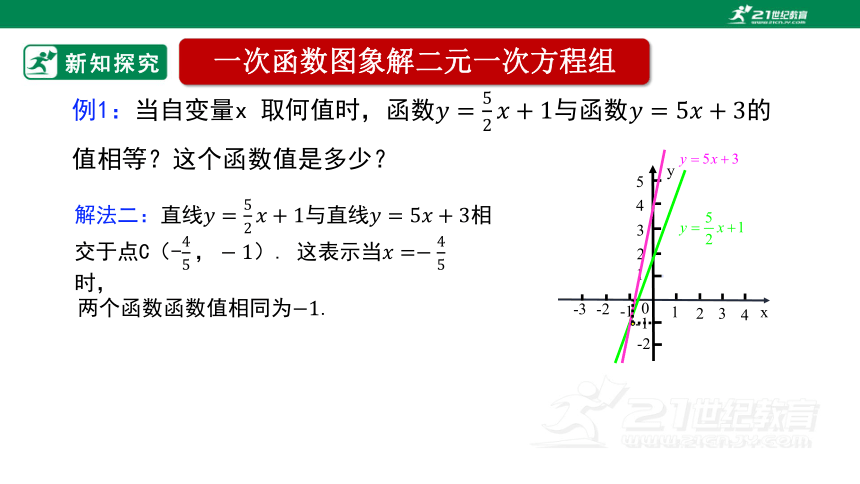
例1:当自变量x 取何值时,函数与函数的值相等?这个函数值是多少?
解法一:联立得到 ,利用代入消元,将方程2代入方程1中,
得,解得.
所以当 时,两个函数函数值相同为.
新知探究
例1:当自变量x 取何值时,函数与函数的值相等?这个函数值是多少?
解法二:直线与直线相交于点C(-). 这表示当 时,
两个函数函数值相同为.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
一次函数图象解二元一次方程组
新知探究
从以上例子可以看出:以二元一次方程组的解作为点的坐标是两个一次函数的交点;反之,两个一次函数的交点坐标是对应的二元一次方程组的解.
新知探究
例2 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系.
(1)气球上升时间满足 .
分析:
1号气球的函数解析式为 ;
2号气球的函数解析式为 .
0≤x ≤60
y=x+5
y=0.5x+15
新知探究
(2)在某个时刻两个气球能否位于同一高度 如果能,这时气球上升了多长时间?位于什么高度?
分析:
(2)在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值.
解二元一次方程组:
y=x+5,
y=0.5x+15,
即:
x-y=-5,
0.5x-y=-15,
解得:
x=20,
y=25,
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
新知探究
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
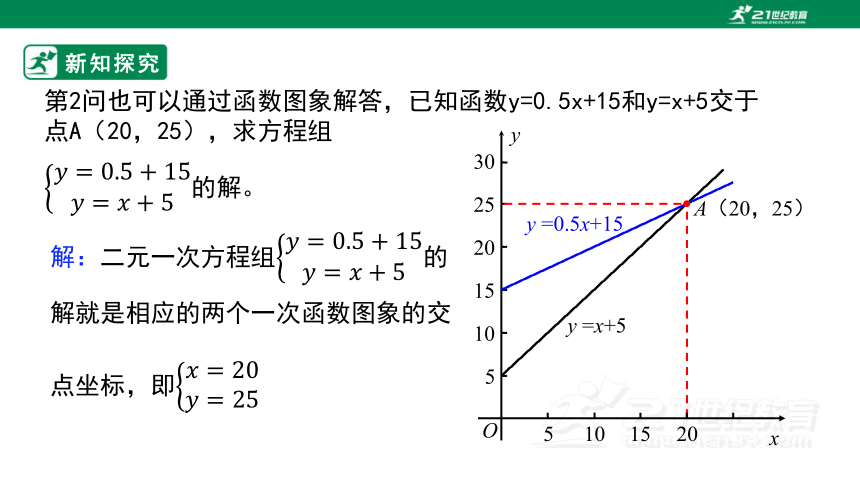
第2问也可以通过函数图象解答,已知函数y=0.5x+15和y=x+5交于点A(20,25),求方程组
的解。
解:二元一次方程组的解就是相应的两个一次函数图象的交点坐标,即
1、如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组 的解是多少?
新知练习
解:此方程组的解是
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
P
y=ax+b
y=cx+d
新知探究
例3 直角坐标系中有两条直线: , ,它们的交点为P,第一条直线交x轴于点A,第二条直线交x轴于点B.
(1)求A,B两点的坐标
(2)用图象法解方程组
(3)求△PAB的面积.
新知探究
解:(1)令y=0,则 ,解得x=-3,
∴点A的坐标为(-3,0),
令y=0,则 ,解得x=4,
∴点B的坐标为(4,0);
(2)结合图象,得方程组的解是
(3)AB=4-(-3)=7,
∴S△PAB= ×7×3= .
课堂总结
从“数”的角度来看
解二元一次方程组,相当于求自变量为何值时对应的两个一次函数相等以及这个函数值是多少的问题.
课堂总结
从“形”的角度来看
解二元一次方程组,相当于确定两条直线的交点坐标,所以可以在同一坐标系中画出两个对应一次函数的图象来求解.
新知练习
新知练习
3. l1和l2分别表示一种白炽灯和一种节能灯的费用 y (元)与照明时间 x (h)的函数图象,假设两种灯的使用寿命都是 2000h,照明效果一样.
(1)根据图象分别求出l1和l2 的
函数解析式;
(2)当照明时间为多少时,两
种灯的费用一样.
新知练习
解:(1)由图可知: l1 经过点(0,2)和(500,17);
l2 经过点(0,20)和(500,26).
设 l1 的函数解析式为 y1=k1x+b1(k10)
则有 解得
b1=2
17=500k1+b1
k1=
b1=2
l1 的函数解析式为y1=x+2.
新知练习
设 l2 的函数解析式为 y2=k2x+b2(k20)
则有 解得
b2=20
26=500k2+b2
k2=
b2=20
l2 的函数解析式为 y2=x+20.
新知练习
(2)由图可知:两种灯的费用一致时也即 l1 和 l2 的交
点坐标.
则有 解得
y1=x+2
y2=x+20
x=1000
y=32
当照明时间为1000h时,费用一样为32元.
课堂总结
一次函数与二元一次方程组
二元一次方程
二元一次方程组
二元一次方程的解对应一次函数图象上的点坐标.
二元一次方程组的解对应两个一次函数图象的交点坐标.
课堂练习
1.一次函数y=kx+3的图象如图所示,则方程kx+3=0的解为 .
3
y=kx+3
O
y
x
3
x=-3
2.若方程组 的解为 则一次函数y=2x+1与y=3x-1的图象交点坐标为______.
(2,5)
课堂练习
3.小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1、l2如图 ,他解的这个方程组是( )
D
点拨:由图象知l1、l2 的 x 的系数都应为负数,排除 A、
C.又 l1、l2的交点为(2,-2),代入验证可知只有 D 符合.
课堂练习
4.利用一次函数的图象解二元一次方程组 .
解析:将方程组中的两个二元一次方程转化为两个一次函数,在同一个坐标系中画出两个一次函数的图象,再利用图象进行求解.
y-2x-1=0
y-x+1=0
课堂练习
解:由方程组,得一次函数 y=2x+1与 y=x-1.
如图,在同一平面直角坐标系中分别画出一次函数 y=2x+1 与 y=x-1 的图象.
它们的交点坐标为(-2,-3),所以二元一次方程组的解为 .
x=-2
y=-3
课堂练习
2.在同一坐标系中分别画出 y1=-2x+1 和 y2=2x-3 的图象,并根据图象回答下列问题.
(1)直线 y1=-2x+1 和 y2=2x-3 分别与 y 轴交于 A、B 两点,请分别写出 A、B 两点的坐标;
(2)写出直线 y1=-2x+1 和 y2=2x-3 的交点 P 的坐标;
(3)求△PAB 的面积.
课堂练习
解:(1)如图,在同一平面直角坐标系中分别画出一次函数 y1=-2x+1 和 y2=2x-3的图象.
它们与 y 轴的交点坐标分别为
A(0,1),B(0,-3).
y
x
O
y1=-2x+1
y2=2x-3
3
3
-3
-3
1
A
B
课堂练习
(2)如图,根据同一平面直角坐标系中一次函数 y1=-2x+1 和 y2=2x-3的图象可知:它们的交点坐标为P(1,-1).
y
x
O
y1=-2x+1
y2=2x-3
3
3
-3
-3
1
A
B
P
课堂练习
(3)根据(1)、(2)可知:
A(0,1),B(0,-3)、P(1,-1),则△PAB 的底边为 AB=4,高为点 P 的
横坐标为1,所以△PAB的面积=
=2.
y
x
O
y1=-2x+1
y2=2x-3
3
3
-3
-3
1
A
B
P
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
19.2.3 一次函数与方程、不等式(3)
人教版八年级下册
知识回顾
1.根据函数 y=2x-1 的图象,利用图象求:
(1)方程 2x-1=0 的解;
(2)不等式 2x-1<0 的解集;
y
x
O
y=2x-1
A
B
1
1
-1
(1)由图象可知,直线y=2x-1与x轴的交点为A(,0),所以方程2x-1=0的解是图象与x轴的交点的横坐标,即x=.
知识回顾
1.根据函数 y=2x-1 的图象,利用图象求:
(1)方程 2x-1=0 的解;
(2)不等式 2x-1<0 的解集;
y
x
O
y=2x-1
A
B
1
1
-1
(2)不等式2x-1<0的解集是函数y=2x-1的图象在x轴下方区域对应的x的取值范围,即x<.
教学目标
1.理解一次函数与二元一次方程(组)的关系.
2.会根据一次函数图象求解二元一次方程(组).
新知导入
二元一次方程 x+y=3 的解有
x=1
y=2
x=-1
y=4
x=0
y=3
x=3
y=0
一次函数 y=-x+3 的图象为:
y
x
O
3
3
y=-x+3
思考:以方程组的解为坐标的点与一次函数的图象有什么关系?
新知小结
从以上例子可以看出:以二元一次方程的解作为点的坐标都在相应的函数图象上;反之,一次函数图象上的点的坐标是对应的二元一次方程的解.
新知探究
例1:当自变量x 取何值时,函数与函数的值相等?这个函数值是多少?
解法一:联立得到 ,利用代入消元,将方程2代入方程1中,
得,解得.
所以当 时,两个函数函数值相同为.
新知探究
例1:当自变量x 取何值时,函数与函数的值相等?这个函数值是多少?
解法二:直线与直线相交于点C(-). 这表示当 时,
两个函数函数值相同为.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
一次函数图象解二元一次方程组
新知探究
从以上例子可以看出:以二元一次方程组的解作为点的坐标是两个一次函数的交点;反之,两个一次函数的交点坐标是对应的二元一次方程组的解.
新知探究
例2 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系.
(1)气球上升时间满足 .
分析:
1号气球的函数解析式为 ;
2号气球的函数解析式为 .
0≤x ≤60
y=x+5
y=0.5x+15
新知探究
(2)在某个时刻两个气球能否位于同一高度 如果能,这时气球上升了多长时间?位于什么高度?
分析:
(2)在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值.
解二元一次方程组:
y=x+5,
y=0.5x+15,
即:
x-y=-5,
0.5x-y=-15,
解得:
x=20,
y=25,
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
新知探究
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
第2问也可以通过函数图象解答,已知函数y=0.5x+15和y=x+5交于点A(20,25),求方程组
的解。
解:二元一次方程组的解就是相应的两个一次函数图象的交点坐标,即
1、如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组 的解是多少?
新知练习
解:此方程组的解是
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
P
y=ax+b
y=cx+d
新知探究
例3 直角坐标系中有两条直线: , ,它们的交点为P,第一条直线交x轴于点A,第二条直线交x轴于点B.
(1)求A,B两点的坐标
(2)用图象法解方程组
(3)求△PAB的面积.
新知探究
解:(1)令y=0,则 ,解得x=-3,
∴点A的坐标为(-3,0),
令y=0,则 ,解得x=4,
∴点B的坐标为(4,0);
(2)结合图象,得方程组的解是
(3)AB=4-(-3)=7,
∴S△PAB= ×7×3= .
课堂总结
从“数”的角度来看
解二元一次方程组,相当于求自变量为何值时对应的两个一次函数相等以及这个函数值是多少的问题.
课堂总结
从“形”的角度来看
解二元一次方程组,相当于确定两条直线的交点坐标,所以可以在同一坐标系中画出两个对应一次函数的图象来求解.
新知练习
新知练习
3. l1和l2分别表示一种白炽灯和一种节能灯的费用 y (元)与照明时间 x (h)的函数图象,假设两种灯的使用寿命都是 2000h,照明效果一样.
(1)根据图象分别求出l1和l2 的
函数解析式;
(2)当照明时间为多少时,两
种灯的费用一样.
新知练习
解:(1)由图可知: l1 经过点(0,2)和(500,17);
l2 经过点(0,20)和(500,26).
设 l1 的函数解析式为 y1=k1x+b1(k10)
则有 解得
b1=2
17=500k1+b1
k1=
b1=2
l1 的函数解析式为y1=x+2.
新知练习
设 l2 的函数解析式为 y2=k2x+b2(k20)
则有 解得
b2=20
26=500k2+b2
k2=
b2=20
l2 的函数解析式为 y2=x+20.
新知练习
(2)由图可知:两种灯的费用一致时也即 l1 和 l2 的交
点坐标.
则有 解得
y1=x+2
y2=x+20
x=1000
y=32
当照明时间为1000h时,费用一样为32元.
课堂总结
一次函数与二元一次方程组
二元一次方程
二元一次方程组
二元一次方程的解对应一次函数图象上的点坐标.
二元一次方程组的解对应两个一次函数图象的交点坐标.
课堂练习
1.一次函数y=kx+3的图象如图所示,则方程kx+3=0的解为 .
3
y=kx+3
O
y
x
3
x=-3
2.若方程组 的解为 则一次函数y=2x+1与y=3x-1的图象交点坐标为______.
(2,5)
课堂练习
3.小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1、l2如图 ,他解的这个方程组是( )
D
点拨:由图象知l1、l2 的 x 的系数都应为负数,排除 A、
C.又 l1、l2的交点为(2,-2),代入验证可知只有 D 符合.
课堂练习
4.利用一次函数的图象解二元一次方程组 .
解析:将方程组中的两个二元一次方程转化为两个一次函数,在同一个坐标系中画出两个一次函数的图象,再利用图象进行求解.
y-2x-1=0
y-x+1=0
课堂练习
解:由方程组,得一次函数 y=2x+1与 y=x-1.
如图,在同一平面直角坐标系中分别画出一次函数 y=2x+1 与 y=x-1 的图象.
它们的交点坐标为(-2,-3),所以二元一次方程组的解为 .
x=-2
y=-3
课堂练习
2.在同一坐标系中分别画出 y1=-2x+1 和 y2=2x-3 的图象,并根据图象回答下列问题.
(1)直线 y1=-2x+1 和 y2=2x-3 分别与 y 轴交于 A、B 两点,请分别写出 A、B 两点的坐标;
(2)写出直线 y1=-2x+1 和 y2=2x-3 的交点 P 的坐标;
(3)求△PAB 的面积.
课堂练习
解:(1)如图,在同一平面直角坐标系中分别画出一次函数 y1=-2x+1 和 y2=2x-3的图象.
它们与 y 轴的交点坐标分别为
A(0,1),B(0,-3).
y
x
O
y1=-2x+1
y2=2x-3
3
3
-3
-3
1
A
B
课堂练习
(2)如图,根据同一平面直角坐标系中一次函数 y1=-2x+1 和 y2=2x-3的图象可知:它们的交点坐标为P(1,-1).
y
x
O
y1=-2x+1
y2=2x-3
3
3
-3
-3
1
A
B
P
课堂练习
(3)根据(1)、(2)可知:
A(0,1),B(0,-3)、P(1,-1),则△PAB 的底边为 AB=4,高为点 P 的
横坐标为1,所以△PAB的面积=
=2.
y
x
O
y1=-2x+1
y2=2x-3
3
3
-3
-3
1
A
B
P
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
