9.2.1 分式的乘除 沪科版七年级数学下册导学课件(共34张PPT)
文档属性
| 名称 | 9.2.1 分式的乘除 沪科版七年级数学下册导学课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 00:00:00 | ||
图片预览







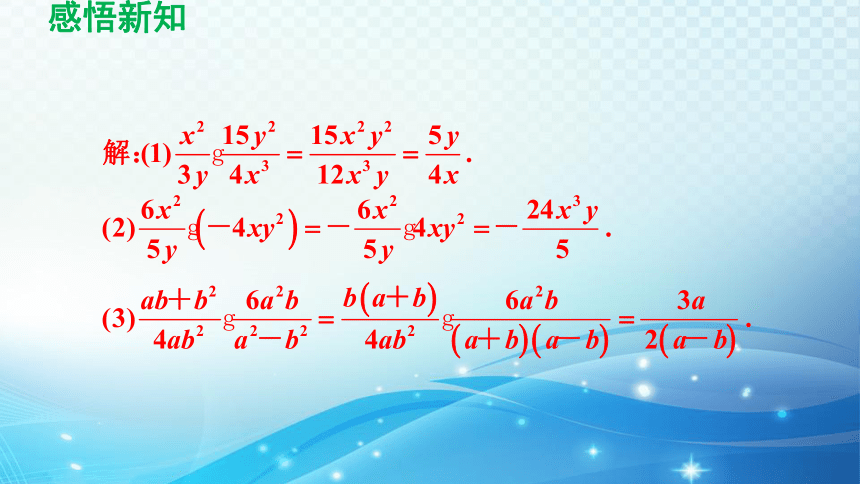




文档简介
(共34张PPT)
9.2 分式的运算
第九章 分式
第1课时
分式的乘除
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
分式的乘法
分式的除法
分式的乘方
分式的乘方、乘除混合运算
知识点
感悟新知
1
分式的乘法
1. 分式的乘法法则 两个分式相乘,用分子的积作为积的分子,分母的积作为积的分母.
用字母表示为
感悟新知
2. 法则的运用方法:
(1)若分子、分母都是单项式,可直接利用乘法法则计算后再约分;
(2)若分子、分母中有多项式,可先对多项式分解因式,看能否约分,再进行乘法运算;
(3)若分式乘整式,可把整式看成分母为1 的“分式”参与运算.
(4)运算的结果应为最简分式或整式 .
感悟新知
特别解读
分式乘法运算的基本步骤:
第 1 步:确定积的符号,写在积中分式的前面;
第2步:运用法则,将分子与分母分别相乘,是多项式的要带括号;
第 3 步:约分,将结果化成最简分式或整式.
感悟新知
计算:
例 1
解题秘方:利用分式的乘法法则进行计算.
感悟新知
感悟新知
知识点
分式的除法
感悟新知
2
1. 分式的除法法则 两个分式相除,将除式的分子、分母颠倒位置后,与被除式相乘.
用字母表示为
感悟新知
2. 法则的运用方法:
(1)分式的除法需转化成乘法,再利用分式乘法法则计算;
(2)当除式是整式时,可以将整式看成分母是1 的“分式”进行运算.
感悟新知
特别提醒
分式除法运算的基本步骤:
第 1 步:将分子、分母是多项式的进行因式分解,并约分;
第 2 步:将除法转化成乘法;
第 3 步:利用分式的乘法法则计算.
感悟新知
计算:
例2
解题秘方:利用分式的除法法则将分式的除法运算转化为分式的乘法运算.
感悟新知
特别提醒
1. 分式的除法与分数的除法类似,可类比分数的除法学习 .
2. 分式的除法法则是数学转化思想的具体体现,即把除法运算转化为乘法运算 .
3. 运算的结果应为最简分式或整式 .
感悟新知
知识点
分式的乘方
感悟新知
3
1. 分式的乘方法则: 分式乘方就是要把分子、分母分别乘方.
用字母表示为 (n 为正整数).
感悟新知
2. 分式乘方的方法:
(1)分式乘方时,确定乘方结果符号的方法与确定有理数乘方结果符号的方法相同;
(2)分式乘方时,一定要将分子、分母分别乘方,不能将
错写成 ;
感悟新知
(3)分式乘方时,若分子与分母是多项式,应把分子、分母分别看成一个整体乘方,避免出现 的错误.
感悟新知
特别解读
1.分式乘方是分式乘法中因式相同时的一种特殊情况,因此分式乘方都可转化为分式乘法进行计算.
2.学习了分式的乘方法则后,可直接用法则计算分式的乘方,在计算时先确定结果的符号,再把分子、分母分别乘方.
感悟新知
计算:
解题秘方:先运用分式的乘方法则将分子、分母分别乘方,再运用幂的乘方和积的乘方的性质计算.
例 3
感悟新知
感悟新知
误答 1:
忘记将分母乘方
误答 2:
负数的奇次方为负,结果应为负
感悟新知
特别警示
在进行乘方运算时,必须将分子、分母整体分别乘方,当分式中含有“-”号时,要特别注意符号问题 .
知识点
分式的乘方、乘除混合运算
感悟新知
4
1. 分式的乘除混合运算 在运算时,乘除是同一级运算,若没有其他附加条件(如括号等),则应按照从左到右的顺序进行计算,若有括号,则先算括号里面的. 一般地,乘除混合运算可以统一为乘法运算.
感悟新知
2. 分式的乘除、乘方混合运算 分式的乘除、乘方混合运算顺序与分数的乘除、乘方混合运算顺序相同,即先算乘方,再算乘除,有括号的先算括号里面的.
感悟新知
知识链接
1.分式的乘除、乘方混合运算关键有两点:一是正确选择运算顺序;二是正确运用运算法则.
2.运算的结果应化为最简分式或整式.
感悟新知
例4
解题秘方:将分式乘除混合运算统一为分式乘法运算 .
感悟新知
感悟新知
技巧提醒
分式的乘除混合运算的解题步骤:
在分式的乘除混合运算中,一定要先将乘除混合运算统一成乘法运算,再按分式乘法法则进行计算,能分解因式的,要分解因式,这样便于约分,计算结果应是最简分式或整式 .
感悟新知
计算:
解题秘方:先算乘方,再算乘除,有括号的先算括号里面的.
例 5
感悟新知
解法提醒
分式乘除、乘方混合运算的解题步骤:
1. 在分式乘除、乘方的混合运算中,先计算乘方,再计算乘除 .
2. 乘、除是同一级运算,要按照从左到右的运算顺序计算 .
3. 当分式中的分子、分母是多项式且能分解因式时,还要分解因式,以达到约分的目的.
感悟新知
感悟新知
本节小结
分式的乘除
分式的乘除
分式的乘方
转化
分式的乘法
混合运算
转化
分式的除法
请完成教材课后习题
作业提升
9.2 分式的运算
第九章 分式
第1课时
分式的乘除
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
分式的乘法
分式的除法
分式的乘方
分式的乘方、乘除混合运算
知识点
感悟新知
1
分式的乘法
1. 分式的乘法法则 两个分式相乘,用分子的积作为积的分子,分母的积作为积的分母.
用字母表示为
感悟新知
2. 法则的运用方法:
(1)若分子、分母都是单项式,可直接利用乘法法则计算后再约分;
(2)若分子、分母中有多项式,可先对多项式分解因式,看能否约分,再进行乘法运算;
(3)若分式乘整式,可把整式看成分母为1 的“分式”参与运算.
(4)运算的结果应为最简分式或整式 .
感悟新知
特别解读
分式乘法运算的基本步骤:
第 1 步:确定积的符号,写在积中分式的前面;
第2步:运用法则,将分子与分母分别相乘,是多项式的要带括号;
第 3 步:约分,将结果化成最简分式或整式.
感悟新知
计算:
例 1
解题秘方:利用分式的乘法法则进行计算.
感悟新知
感悟新知
知识点
分式的除法
感悟新知
2
1. 分式的除法法则 两个分式相除,将除式的分子、分母颠倒位置后,与被除式相乘.
用字母表示为
感悟新知
2. 法则的运用方法:
(1)分式的除法需转化成乘法,再利用分式乘法法则计算;
(2)当除式是整式时,可以将整式看成分母是1 的“分式”进行运算.
感悟新知
特别提醒
分式除法运算的基本步骤:
第 1 步:将分子、分母是多项式的进行因式分解,并约分;
第 2 步:将除法转化成乘法;
第 3 步:利用分式的乘法法则计算.
感悟新知
计算:
例2
解题秘方:利用分式的除法法则将分式的除法运算转化为分式的乘法运算.
感悟新知
特别提醒
1. 分式的除法与分数的除法类似,可类比分数的除法学习 .
2. 分式的除法法则是数学转化思想的具体体现,即把除法运算转化为乘法运算 .
3. 运算的结果应为最简分式或整式 .
感悟新知
知识点
分式的乘方
感悟新知
3
1. 分式的乘方法则: 分式乘方就是要把分子、分母分别乘方.
用字母表示为 (n 为正整数).
感悟新知
2. 分式乘方的方法:
(1)分式乘方时,确定乘方结果符号的方法与确定有理数乘方结果符号的方法相同;
(2)分式乘方时,一定要将分子、分母分别乘方,不能将
错写成 ;
感悟新知
(3)分式乘方时,若分子与分母是多项式,应把分子、分母分别看成一个整体乘方,避免出现 的错误.
感悟新知
特别解读
1.分式乘方是分式乘法中因式相同时的一种特殊情况,因此分式乘方都可转化为分式乘法进行计算.
2.学习了分式的乘方法则后,可直接用法则计算分式的乘方,在计算时先确定结果的符号,再把分子、分母分别乘方.
感悟新知
计算:
解题秘方:先运用分式的乘方法则将分子、分母分别乘方,再运用幂的乘方和积的乘方的性质计算.
例 3
感悟新知
感悟新知
误答 1:
忘记将分母乘方
误答 2:
负数的奇次方为负,结果应为负
感悟新知
特别警示
在进行乘方运算时,必须将分子、分母整体分别乘方,当分式中含有“-”号时,要特别注意符号问题 .
知识点
分式的乘方、乘除混合运算
感悟新知
4
1. 分式的乘除混合运算 在运算时,乘除是同一级运算,若没有其他附加条件(如括号等),则应按照从左到右的顺序进行计算,若有括号,则先算括号里面的. 一般地,乘除混合运算可以统一为乘法运算.
感悟新知
2. 分式的乘除、乘方混合运算 分式的乘除、乘方混合运算顺序与分数的乘除、乘方混合运算顺序相同,即先算乘方,再算乘除,有括号的先算括号里面的.
感悟新知
知识链接
1.分式的乘除、乘方混合运算关键有两点:一是正确选择运算顺序;二是正确运用运算法则.
2.运算的结果应化为最简分式或整式.
感悟新知
例4
解题秘方:将分式乘除混合运算统一为分式乘法运算 .
感悟新知
感悟新知
技巧提醒
分式的乘除混合运算的解题步骤:
在分式的乘除混合运算中,一定要先将乘除混合运算统一成乘法运算,再按分式乘法法则进行计算,能分解因式的,要分解因式,这样便于约分,计算结果应是最简分式或整式 .
感悟新知
计算:
解题秘方:先算乘方,再算乘除,有括号的先算括号里面的.
例 5
感悟新知
解法提醒
分式乘除、乘方混合运算的解题步骤:
1. 在分式乘除、乘方的混合运算中,先计算乘方,再计算乘除 .
2. 乘、除是同一级运算,要按照从左到右的运算顺序计算 .
3. 当分式中的分子、分母是多项式且能分解因式时,还要分解因式,以达到约分的目的.
感悟新知
感悟新知
本节小结
分式的乘除
分式的乘除
分式的乘方
转化
分式的乘法
混合运算
转化
分式的除法
请完成教材课后习题
作业提升
