9.1.2 不等式的性质 初中数学人教版七年级下册教案(表格式)
文档属性
| 名称 | 9.1.2 不等式的性质 初中数学人教版七年级下册教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-07 00:00:00 | ||
图片预览

文档简介
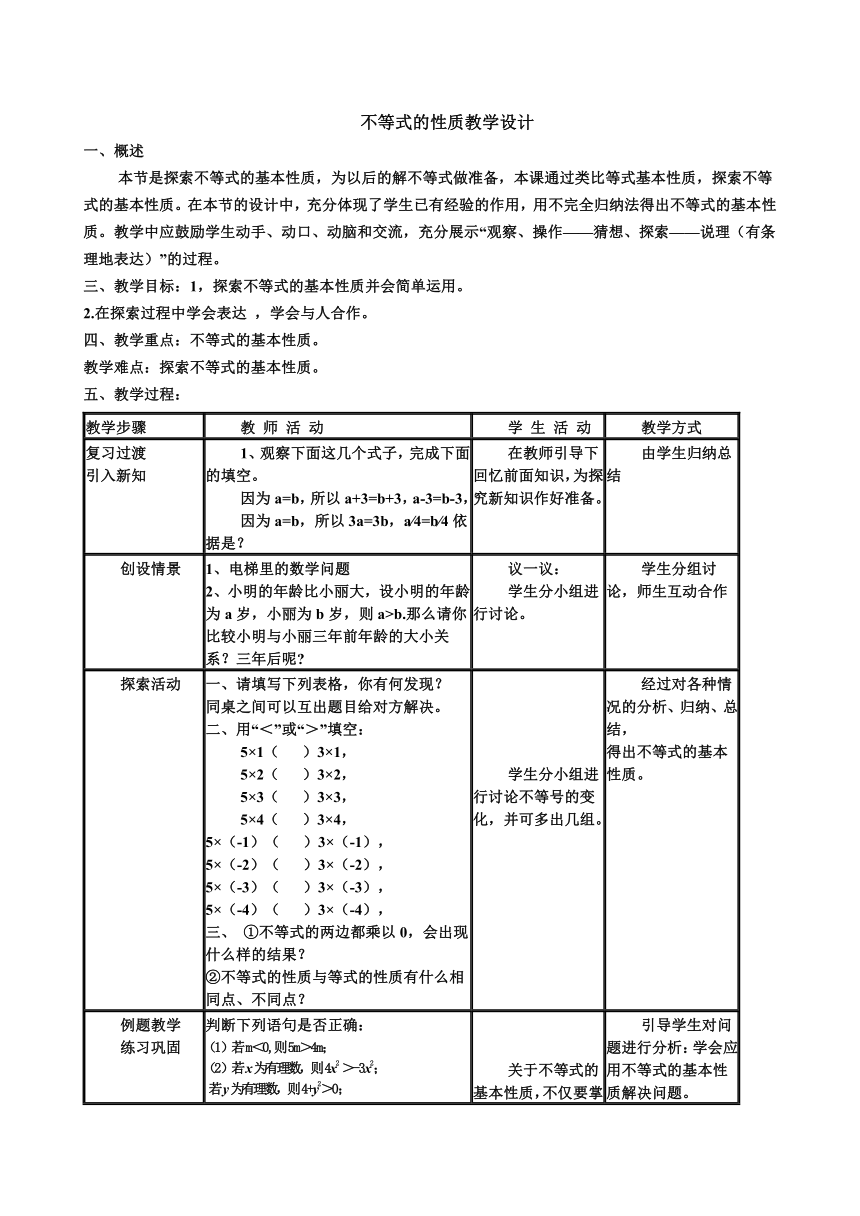
不等式的性质教学设计一、概述本节是探索不等式的基本性质,为以后的解不等式做准备,本课通过类比等式基本性质,探索不等式的基本性质。在本节的设计中,充分体现了学生已有经验的作用,用不完全归纳法得出不等式的基本性质。教学中应鼓励学生动手、动口、动脑和交流,充分展示“观察、操作——猜想、探索——说理(有条理地表达)”的过程。三、教学目标:1,探索不等式的基本性质并会简单运用。2.在探索过程中学会表达 ,学会与人合作。四、教学重点:不等式的基本性质。教学难点:探索不等式的基本性质。五、教学过程:教学步骤教 师 活 动学 生 活 动教学方式复习过渡引入新知1、观察下面这几个式子,完成下面的填空。因为a=b,所以a+3=b+3,a-3=b-3,因为a=b,所以3a=3b,a∕4=b∕4依据是?在教师引导下回忆前面知识,为探究新知识作好准备。由学生归纳总结创设情景1、电梯里的数学问题2、小明的年龄比小丽大,设小明的年龄为a岁,小丽为b岁,则a>b.那么请你比较小明与小丽三年前年龄的大小关系?三年后呢 议一议:学生分小组进行讨论。学生分组讨论,师生互动合作探索活动一、请填写下列表格,你有何发现?同桌之间可以互出题目给对方解决。二、用“<”或“>”填空: 5×1( )3×1,5×2( )3×2,5×3( )3×3,5×4( )3×4,5×(-1)( )3×(-1),5×(-2)( )3×(-2),5×(-3)( )3×(-3),5×(-4)( )3×(-4),三、 ①不等式的两边都乘以0,会出现什么样的结果?②不等式的性质与等式的性质有什么相同点、不同点?学生分小组进行讨论不等号的变化,并可多出几组。经过对各种情况的分析、归纳、总结,得出不等式的基本性质。例题教学练习巩固判断下列语句是否正确:将下列不等式化成“x>a”或“x<a”的形式:(1)x-5>-1; (2)-2x>3; (3)3x<-9. 2 用“>”或“<”填空:(1)a+3_____b+3(ab);(3) (a>b); (4)a-4_____b-4 (a-b>0) ; (5)若b<0,则a+b_____a; 练习:1、 2、将不等式 ax ≥ x +4化成“x≥m”或“x≤n”的形式. 下面是阿华学完本节后的解答,让我们一起来批改. 解:根据不等式的性质1,两边都减去x,得: ax - x≥ x – x+4 即:(a – 1)x ≥ +4根据不等式的性质2,两边都除以(a-1),得: 拓展延伸:1.已知a>b,能否推出ac2>bc2 2.已知ac2>bc2,能否推出a>b 3.已知x>5,能否推出2x-3>74.已知x<2,能否推出3-2x>-1 关于不等式的基本性质,不仅要掌握其内容,还要会应用。引导学生对问题进行分析:学会应用不等式的基本性质解决问题。反思小结提炼规律不等式的基本性质是什么 和等式的基本性质相比,有什么相同和不同之处 本节课你还有什么收获 教师带领,回顾反思本节课对知识的研究探索过程,小结方法及结论,提炼数学思想,掌握数学规律。作业布置教师带领,回顾反思本节课对知识的研究探索过程,小结方法及结论,提炼数学思想,掌握数学规律。学生在教师引导下回顾反思,归纳整理。教学反思类比教学是否能达到预期效果从数到字母看似容易,但是一旦变成字母,学生未必掌握很好学生对不等式的性质特别是第三条性质还有加以巩固学习不等式的性质有何作用?学生能否意会到其中的道理
