8.1.2样本相关系数 教学课件(共25张PPT)
文档属性
| 名称 | 8.1.2样本相关系数 教学课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 16:50:30 | ||
图片预览







文档简介
第八章成对数据的统计分析
8.1.2样本相关系数
李思
目录
CONTENT
03
04
01
02
典型例题
课堂总结
知识回顾
样本相关系数
知识回顾
PART.01
知识回顾
1.变量间的相关关系是什么?
2.散点图是什么?
3.变量相关关系的分类是什么?
正相关
线性相关
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
成对样本数据可用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图。
非线性相关
负相关
问题引入
散点图可以说明变量间有无线性相关关系,但无法量化两个变量之间的相关程度的大小,更不能精确地说明成对样本数据之间关系的密切程度,那么我们如何才能寻找到这样一个合适的量来对样本数据的相关程度进行定量分析呢?
问题引入
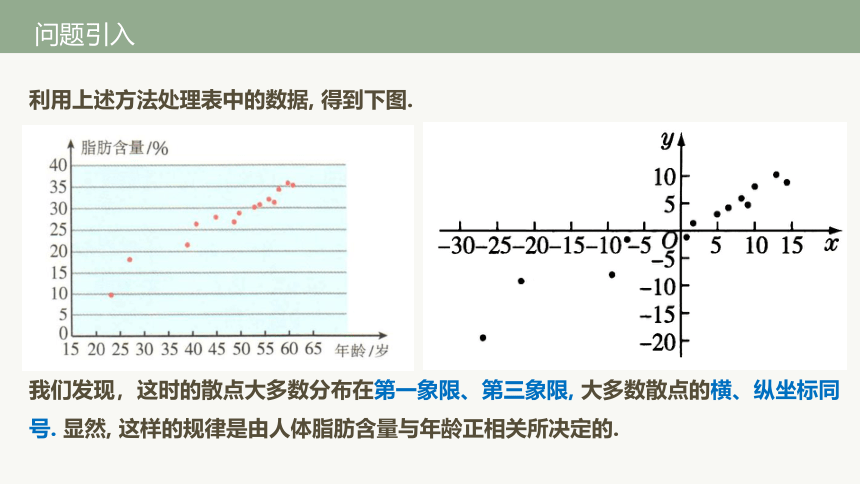
利用上述方法处理表中的数据, 得到下图.
我们发现,这时的散点大多数分布在第一象限、第三象限, 大多数散点的横、纵坐标同号. 显然, 这样的规律是由人体脂肪含量与年龄正相关所决定的.
问题引入
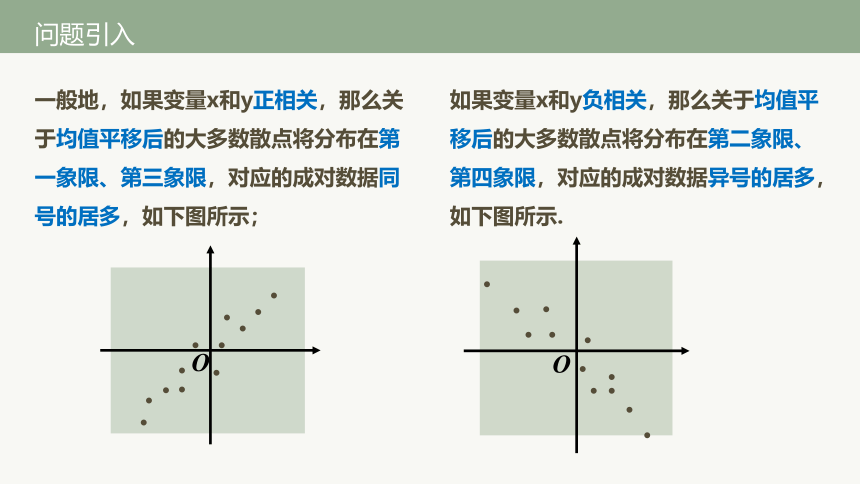
一般地,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第一象限、第三象限,对应的成对数据同号的居多,如下图所示;
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
如果变量x和y负相关,那么关于均值平移后的大多数散点将分布在第二象限、第四象限,对应的成对数据异号的居多,如下图所示.
问题引入
思考:根据上述分析,你能利用正相关变量和负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗?
思考:你认为Lxy的大小一定能度量出成对样本数据的相关程度吗?
Lxy的大小与数据的度量有关,故不宜直接用它度量成对样本数据相关程度的大小.
例如,在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,则相应的Lxy将变为原来的100倍,但单位的改变并不会导致体重与身高之间相关程度的改变.
问题引入
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
????????=????????????=????????(?????????????)????,????????=????????????=????????(?????????????)????分别除?????????????和?????????????(????=????,????,?,????),
得(?????????????????????,?????????????????????),(?????????????????????,?????????????????????),?,(?????????????????????,?????????????????????).
?
把上述“标准化”处理后的成对数据分别记为(????????’,????????’),(????????’,????????’),?,(????????’,????????’),仿照????????????的构造,可以得到
????=????????(????????’????????’+????????’????????’+?+????????’????????’)=????=????????(?????????????)(?????????????)????=????????(?????????????)????????=????????(?????????????)????.(1)
我们称????为变量x和变量y的样本相关系数.
?
样本相关系数
PART.02
样本相关系数
对于变量x,y,利用成对样本数据(x1,y1),(x2,y2),…,(xn,yn)构造
则称r为变量x和变量y的样本相关系数.
(1)当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
(2)取值范围为[-1,1]:
当|r|越接近1时,线性相关程度越强,当|r|越接近0时,线性相关程度越弱.当|r|=1时,表明成对样本数据都落在一条直线上;当r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
样本相关系数
典例1:两个变量之间的相关程度越低,则其线性相关系数的数值( )
A.越小 B.越接近1 C.越接近0 D.越接近-1
典例2:给定y与x的一组样本数据,求得相关系数r=-0.690,则( )
A.y与x线性不相关 B.y与x正线性相关
C.y与x负线性相关 D.以上都不对
C
C
典例3:(多选题)下列说法正确的是( )
A.变量间的关系是非确定性关系,因此因变量不能由自变量唯一确定
B.线性相关系数可以是正的或负的
C.如果r=±1,说明x与y之间完全线性相关
D.线性相关系数r∈(-1,1)
ABC
典型例题
PART.03
样本相关系数
例1:画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本相关系数在刻画成对样本数据相关关系上的特点.
(1) (-2, -3), (-1, -1), (0, 1), (1, 3), (2, 5), (3, 7);
2
4
8
x
-4
-3
2
0
-2
1
3
-1
6
y
-2
?
?
?
?
?
?
r=1
样本相关系数
例1:画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本相关系数在刻画成对样本数据相关关系上的特点.
(2) (0, 0), (1, 1), (2, 4), (3, 9), (4, 16);
r=0.96
5
15
x
2
0
4
1
3
10
y
?
?
?
?
?
样本相关系数
例1:画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本相关系数在刻画成对样本数据相关关系上的特点.
(3) (-2, -8), (-1, -1), (0, 0), (1, 1), (2, 8), (3, 27);
r=0.89
5
10
20
x
-10
-3
2
0
-2
1
3
-1
15
y
-5
?
?
?
?
?
?
25
样本相关系数
例2:关于两个变量x和y的7组数据如下表所示:
计算两个变量的样本相关关系,并据此判断????与????之间是否具有线性相关关系.
?
解:∵????=????????×(????????+????????+????????+????????+????????+????????+????????)≈????????.????,
????=????????×(????+????????+????????+????????+????????+????????????+????????????)≈????????.????,
????=????????????????????=????????????+????????????+????????????+????????????+????????????+????????????+????????????=????????????????,
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
21
23
25
27
29
32
35
????
7
11
21
24
66
115
325
样本相关系数
解:∵????=????????????????????????=????????×????+????????×????????+????????×????????+????????×????????+????????×????????+????????×????????????+????????×????????????=????????????????????,
????=????????????????????=????????+????????????+????????????+????????????+????????????+????????????????+????????????????=????????????????????????,
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
21
23
25
27
29
32
35
????
7
11
21
24
66
115
325
∴????=????=?????????????????????????????????????????=?????????????????????????????????????=?????????????????????????????????=?????????????????????????×????????.????×????????.?????????????????????????×????????.?????????????????????????????????????×????????.????????≈????.????????????????.
由于????≈????.????????????????与????比较接近,∴????与????具有线性相关关系.
?
样本相关系数
例3:某校高三(1)班的学生每周用于数学学习的时间????(单位:????)与数学平均成绩????(单位:分)之间如表格所示的数据.
(1)画出散点图;(2)请判断数学学习的时间与数学平均成绩之间的相关关系的类型、相关程度和变化趋势的特征.
?
解:(1):根据表中的数据画出散点图,如图.
从散点图看,数学成绩与学习时间线性相关.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
24
15
23
19
16
11
20
16
17
13
????
92
79
97
89
64
47
83
68
71
59
样本相关系数
(2):由已知数据求得????=????????.????,????=????????.????,????=????????????????????????=????????????????,????=????????????????????????=????????????????????,
????=????????????????????????????=????????????????????,所以相关系数????=????=?????????????????????????????????????????????(????=?????????????????????????????????????????)(????=?????????????????????????????????????????)≈????.????????????.
由相关系数知,数学学习时间与数学平均成绩呈正线性相关,因为????≈????.????????????与1接近,所以数学学习时间与数学成绩相关程度很高,且随着学习时间的增加,相应的学习成绩升高.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
24
15
23
19
16
11
20
16
17
13
????
92
79
97
89
64
47
83
68
71
59
样本相关系数
例4:有一个同学家开了一个小卖部,他为了研究气温对热饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的数据如表所示.
(1)画出散点图;
(2)用相关系数????判断热饮杯数与当天气温的关系的强弱.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}摄氏温度????
-5
4
7
10
15
23
30
36
热饮杯数????
162
128
115
135
89
71
63
37
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}摄氏温度????
-5
4
7
10
15
23
30
36
162
128
115
135
89
71
63
37
样本相关系数
(2):由数据得????=????????×(?????+????+????+????????+????????+????????+????????+????????)=????????,
????=????????×(????????????+????????????+????????????+????????????+????????+????????+????????+????????)=????????????,
代入????的计算公式得????=????=????????(?????????????)(?????????????)????=????????(?????????????)????????=????????(?????????????)????≈?????????????????????????????????×????????????≈?????.????????,
所以气温与当天热饮销售杯数得负相关很强.
?
解:(1)散点图如图所示.
课堂总结
PART.04
课堂总结
1.样本相关系数;
2.样本相关系数的应用。
统计学是对令人困惑费解的问题做出数字设想的艺术。
李思
THANK
8.1.2样本相关系数
李思
目录
CONTENT
03
04
01
02
典型例题
课堂总结
知识回顾
样本相关系数
知识回顾
PART.01
知识回顾
1.变量间的相关关系是什么?
2.散点图是什么?
3.变量相关关系的分类是什么?
正相关
线性相关
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
成对样本数据可用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图。
非线性相关
负相关
问题引入
散点图可以说明变量间有无线性相关关系,但无法量化两个变量之间的相关程度的大小,更不能精确地说明成对样本数据之间关系的密切程度,那么我们如何才能寻找到这样一个合适的量来对样本数据的相关程度进行定量分析呢?
问题引入
利用上述方法处理表中的数据, 得到下图.
我们发现,这时的散点大多数分布在第一象限、第三象限, 大多数散点的横、纵坐标同号. 显然, 这样的规律是由人体脂肪含量与年龄正相关所决定的.
问题引入
一般地,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第一象限、第三象限,对应的成对数据同号的居多,如下图所示;
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
如果变量x和y负相关,那么关于均值平移后的大多数散点将分布在第二象限、第四象限,对应的成对数据异号的居多,如下图所示.
问题引入
思考:根据上述分析,你能利用正相关变量和负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗?
思考:你认为Lxy的大小一定能度量出成对样本数据的相关程度吗?
Lxy的大小与数据的度量有关,故不宜直接用它度量成对样本数据相关程度的大小.
例如,在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,则相应的Lxy将变为原来的100倍,但单位的改变并不会导致体重与身高之间相关程度的改变.
问题引入
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
????????=????????????=????????(?????????????)????,????????=????????????=????????(?????????????)????分别除?????????????和?????????????(????=????,????,?,????),
得(?????????????????????,?????????????????????),(?????????????????????,?????????????????????),?,(?????????????????????,?????????????????????).
?
把上述“标准化”处理后的成对数据分别记为(????????’,????????’),(????????’,????????’),?,(????????’,????????’),仿照????????????的构造,可以得到
????=????????(????????’????????’+????????’????????’+?+????????’????????’)=????=????????(?????????????)(?????????????)????=????????(?????????????)????????=????????(?????????????)????.(1)
我们称????为变量x和变量y的样本相关系数.
?
样本相关系数
PART.02
样本相关系数
对于变量x,y,利用成对样本数据(x1,y1),(x2,y2),…,(xn,yn)构造
则称r为变量x和变量y的样本相关系数.
(1)当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
(2)取值范围为[-1,1]:
当|r|越接近1时,线性相关程度越强,当|r|越接近0时,线性相关程度越弱.当|r|=1时,表明成对样本数据都落在一条直线上;当r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
样本相关系数
典例1:两个变量之间的相关程度越低,则其线性相关系数的数值( )
A.越小 B.越接近1 C.越接近0 D.越接近-1
典例2:给定y与x的一组样本数据,求得相关系数r=-0.690,则( )
A.y与x线性不相关 B.y与x正线性相关
C.y与x负线性相关 D.以上都不对
C
C
典例3:(多选题)下列说法正确的是( )
A.变量间的关系是非确定性关系,因此因变量不能由自变量唯一确定
B.线性相关系数可以是正的或负的
C.如果r=±1,说明x与y之间完全线性相关
D.线性相关系数r∈(-1,1)
ABC
典型例题
PART.03
样本相关系数
例1:画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本相关系数在刻画成对样本数据相关关系上的特点.
(1) (-2, -3), (-1, -1), (0, 1), (1, 3), (2, 5), (3, 7);
2
4
8
x
-4
-3
2
0
-2
1
3
-1
6
y
-2
?
?
?
?
?
?
r=1
样本相关系数
例1:画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本相关系数在刻画成对样本数据相关关系上的特点.
(2) (0, 0), (1, 1), (2, 4), (3, 9), (4, 16);
r=0.96
5
15
x
2
0
4
1
3
10
y
?
?
?
?
?
样本相关系数
例1:画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本相关系数在刻画成对样本数据相关关系上的特点.
(3) (-2, -8), (-1, -1), (0, 0), (1, 1), (2, 8), (3, 27);
r=0.89
5
10
20
x
-10
-3
2
0
-2
1
3
-1
15
y
-5
?
?
?
?
?
?
25
样本相关系数
例2:关于两个变量x和y的7组数据如下表所示:
计算两个变量的样本相关关系,并据此判断????与????之间是否具有线性相关关系.
?
解:∵????=????????×(????????+????????+????????+????????+????????+????????+????????)≈????????.????,
????=????????×(????+????????+????????+????????+????????+????????????+????????????)≈????????.????,
????=????????????????????=????????????+????????????+????????????+????????????+????????????+????????????+????????????=????????????????,
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
21
23
25
27
29
32
35
????
7
11
21
24
66
115
325
样本相关系数
解:∵????=????????????????????????=????????×????+????????×????????+????????×????????+????????×????????+????????×????????+????????×????????????+????????×????????????=????????????????????,
????=????????????????????=????????+????????????+????????????+????????????+????????????+????????????????+????????????????=????????????????????????,
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
21
23
25
27
29
32
35
????
7
11
21
24
66
115
325
∴????=????=?????????????????????????????????????????=?????????????????????????????????????=?????????????????????????????????=?????????????????????????×????????.????×????????.?????????????????????????×????????.?????????????????????????????????????×????????.????????≈????.????????????????.
由于????≈????.????????????????与????比较接近,∴????与????具有线性相关关系.
?
样本相关系数
例3:某校高三(1)班的学生每周用于数学学习的时间????(单位:????)与数学平均成绩????(单位:分)之间如表格所示的数据.
(1)画出散点图;(2)请判断数学学习的时间与数学平均成绩之间的相关关系的类型、相关程度和变化趋势的特征.
?
解:(1):根据表中的数据画出散点图,如图.
从散点图看,数学成绩与学习时间线性相关.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
24
15
23
19
16
11
20
16
17
13
????
92
79
97
89
64
47
83
68
71
59
样本相关系数
(2):由已知数据求得????=????????.????,????=????????.????,????=????????????????????????=????????????????,????=????????????????????????=????????????????????,
????=????????????????????????????=????????????????????,所以相关系数????=????=?????????????????????????????????????????????(????=?????????????????????????????????????????)(????=?????????????????????????????????????????)≈????.????????????.
由相关系数知,数学学习时间与数学平均成绩呈正线性相关,因为????≈????.????????????与1接近,所以数学学习时间与数学成绩相关程度很高,且随着学习时间的增加,相应的学习成绩升高.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
24
15
23
19
16
11
20
16
17
13
????
92
79
97
89
64
47
83
68
71
59
样本相关系数
例4:有一个同学家开了一个小卖部,他为了研究气温对热饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的数据如表所示.
(1)画出散点图;
(2)用相关系数????判断热饮杯数与当天气温的关系的强弱.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}摄氏温度????
-5
4
7
10
15
23
30
36
热饮杯数????
162
128
115
135
89
71
63
37
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}摄氏温度????
-5
4
7
10
15
23
30
36
162
128
115
135
89
71
63
37
样本相关系数
(2):由数据得????=????????×(?????+????+????+????????+????????+????????+????????+????????)=????????,
????=????????×(????????????+????????????+????????????+????????????+????????+????????+????????+????????)=????????????,
代入????的计算公式得????=????=????????(?????????????)(?????????????)????=????????(?????????????)????????=????????(?????????????)????≈?????????????????????????????????×????????????≈?????.????????,
所以气温与当天热饮销售杯数得负相关很强.
?
解:(1)散点图如图所示.
课堂总结
PART.04
课堂总结
1.样本相关系数;
2.样本相关系数的应用。
统计学是对令人困惑费解的问题做出数字设想的艺术。
李思
THANK
