8.3.1分类变量与列联表 教学课件(共17张PPT)
文档属性
| 名称 | 8.3.1分类变量与列联表 教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 335.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 16:51:13 | ||
图片预览






文档简介
(共17张PPT)
第八章成对数据的统计分析
8.3.1分类变量与列联表
李思
目录
CONTENT
03
04
01
02
典型例题
课堂总结
知识回顾
分类变量
与列联表
引言
PART.01
引言
前面两节所讨论的变量 , 如人的身高、树的高度、短跑100m世界纪录和创纪录的时间等, 都是数值变量, 数值变量的取值为实数. 其大小和运算都有实际含义.
在现实生活中 , 人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题. 例如 ,就读不同学校是否对学生的成绩有影响 , 不同班级学生用于体育锻炼的时间是否有差别 , 吸烟是否会增加患肺癌的风险 , 等等 , 本节将要学习的独立性检验方法为我们提供了解决这类问题的方案.
数值变量:数值变量的取值为实数,其大小和运算都有实际含义.
分类变量:这里所说的变量和值不一定是具体的数值,例如:性别变量,其取值为男和女两种,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量,分类变量的取值可以用实数表示.
分类变量与列联表
PART.02
问题
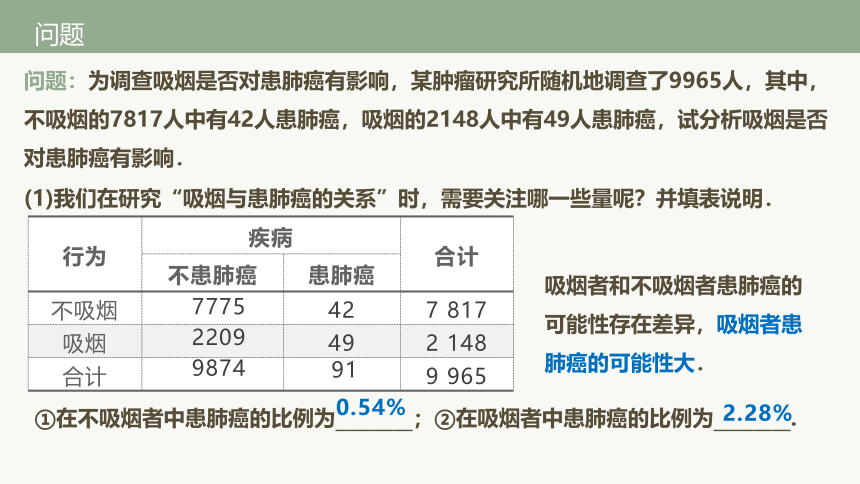
问题:为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,其中,不吸烟的7817人中有42人患肺癌,吸烟的2148人中有49人患肺癌,试分析吸烟是否对患肺癌有影响.
(1)我们在研究“吸烟与患肺癌的关系”时,需要关注哪一些量呢?并填表说明.
行为 疾病 合计
不患肺癌 患肺癌 不吸烟 42 7 817
吸烟 49 2 148
合计 9 965
①在不吸烟者中患肺癌的比例为________;②在吸烟者中患肺癌的比例为________.
7775
2209
9874
91
0.54%
2.28%
吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大.
2×2列联表
定义一对分类变量X和Y,我们整理数据如表所示:
X Y 合计
Y=0 Y=1 X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
上表是关于分类变量X和Y的抽样数据的2×2列联表:
最后一行的前两个数分别是事件{Y=0}和{Y=1}的频数;
最后一列的前两个数分别是事件{X=0}和{X=1}的频数;
中间的四个数a,b,c,d是事件{X=x,Y=y}(x,y=0,1)的频数;
右下角格中的数n是样本容量.
注意:列联表是两个或两个以上分类变量的汇总统计表,现阶段我们仅研究两个分类变量的列联表,并且每个分类变量只取两个值.
2×2列联表
典例1:在一项有关医疗保健的社会调查中,发现调查的男性为530人,女性为670人,其中男性中喜欢吃甜食的为117人,女性中喜欢吃甜食的为492人,则性别与喜欢吃甜食的2×2列联表为________.
喜欢吃甜食 不喜欢吃甜食 合计
男 117 413 530
女 492 178 670
合计 609 591 1 200
问题
思考:我们还能够用图形得到吸烟与患肺癌之间的关系吗?
等高堆积条形图
等高堆积条形图和表格相比,更能直观地反映出两个分类变量间是否相互影响,常用等高堆积条形图展示列联表数据的频率特征,依据频率稳定于概率的原理,我们可以推断结果.
等高堆积条形图
典例2:网络对现代人的生活影响较大,尤其是对青少年,为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生中随机抽取了1 000人调查,发现其中经常上网的有200人,这200人中有80人期末考试不及格,而另外800人中有120人不及格.利用等高堆积条形图判断学生学习成绩与经常上网有关吗?
解:根据题目所给的数据得到如下2×2列联表:
学习成绩 上网 合计
经常 不经常 不及格 80 120 200
及格 120 680 800
合计 200 800 1 000
等高堆积条形图
经常上网的学生中期末考试不及格和及格的频率分别为0.4和0.6;不经常上网的学生中期末考试不及格和及格的频率分别为0.15和0.85.
比较图中阴影部分的高可以发现经常上网学生的成绩不及格的频率明显高于不经常上网学生的成绩不及格的频率,因此可以认为学习成绩与经常上网有关.
学习成绩 上网 合计
经常 不经常 不及格 80 120 200
及格 120 680 800
合计 200 800 1 000
典型例题
PART.03
2×2列联表与等高堆积条形图
例1:下面是一个2×2列联表:
X Y 合计
Y=0 Y=1 X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为( )A.94,96 B.52,50 C.52,60 D.54,52
C
2×2列联表与等高堆积条形图
例2:已知两个分类变量X,Y,它们的取值分别为{x1,x2}和{y1,y2},观察下列各图,其中两个分类变量X,Y之间关系最强的是( )
D
课堂总结
PART.04
课堂总结
1.分类变量与数值变量;
2.2×2列联表;
3.等高堆积条形图。
4.2×2列联表与等高堆积条形图的实际应用。
统计学是对令人困惑费解的问题做出数字设想的艺术。
李思
THANK
第八章成对数据的统计分析
8.3.1分类变量与列联表
李思
目录
CONTENT
03
04
01
02
典型例题
课堂总结
知识回顾
分类变量
与列联表
引言
PART.01
引言
前面两节所讨论的变量 , 如人的身高、树的高度、短跑100m世界纪录和创纪录的时间等, 都是数值变量, 数值变量的取值为实数. 其大小和运算都有实际含义.
在现实生活中 , 人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题. 例如 ,就读不同学校是否对学生的成绩有影响 , 不同班级学生用于体育锻炼的时间是否有差别 , 吸烟是否会增加患肺癌的风险 , 等等 , 本节将要学习的独立性检验方法为我们提供了解决这类问题的方案.
数值变量:数值变量的取值为实数,其大小和运算都有实际含义.
分类变量:这里所说的变量和值不一定是具体的数值,例如:性别变量,其取值为男和女两种,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量,分类变量的取值可以用实数表示.
分类变量与列联表
PART.02
问题
问题:为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,其中,不吸烟的7817人中有42人患肺癌,吸烟的2148人中有49人患肺癌,试分析吸烟是否对患肺癌有影响.
(1)我们在研究“吸烟与患肺癌的关系”时,需要关注哪一些量呢?并填表说明.
行为 疾病 合计
不患肺癌 患肺癌 不吸烟 42 7 817
吸烟 49 2 148
合计 9 965
①在不吸烟者中患肺癌的比例为________;②在吸烟者中患肺癌的比例为________.
7775
2209
9874
91
0.54%
2.28%
吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大.
2×2列联表
定义一对分类变量X和Y,我们整理数据如表所示:
X Y 合计
Y=0 Y=1 X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
上表是关于分类变量X和Y的抽样数据的2×2列联表:
最后一行的前两个数分别是事件{Y=0}和{Y=1}的频数;
最后一列的前两个数分别是事件{X=0}和{X=1}的频数;
中间的四个数a,b,c,d是事件{X=x,Y=y}(x,y=0,1)的频数;
右下角格中的数n是样本容量.
注意:列联表是两个或两个以上分类变量的汇总统计表,现阶段我们仅研究两个分类变量的列联表,并且每个分类变量只取两个值.
2×2列联表
典例1:在一项有关医疗保健的社会调查中,发现调查的男性为530人,女性为670人,其中男性中喜欢吃甜食的为117人,女性中喜欢吃甜食的为492人,则性别与喜欢吃甜食的2×2列联表为________.
喜欢吃甜食 不喜欢吃甜食 合计
男 117 413 530
女 492 178 670
合计 609 591 1 200
问题
思考:我们还能够用图形得到吸烟与患肺癌之间的关系吗?
等高堆积条形图
等高堆积条形图和表格相比,更能直观地反映出两个分类变量间是否相互影响,常用等高堆积条形图展示列联表数据的频率特征,依据频率稳定于概率的原理,我们可以推断结果.
等高堆积条形图
典例2:网络对现代人的生活影响较大,尤其是对青少年,为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生中随机抽取了1 000人调查,发现其中经常上网的有200人,这200人中有80人期末考试不及格,而另外800人中有120人不及格.利用等高堆积条形图判断学生学习成绩与经常上网有关吗?
解:根据题目所给的数据得到如下2×2列联表:
学习成绩 上网 合计
经常 不经常 不及格 80 120 200
及格 120 680 800
合计 200 800 1 000
等高堆积条形图
经常上网的学生中期末考试不及格和及格的频率分别为0.4和0.6;不经常上网的学生中期末考试不及格和及格的频率分别为0.15和0.85.
比较图中阴影部分的高可以发现经常上网学生的成绩不及格的频率明显高于不经常上网学生的成绩不及格的频率,因此可以认为学习成绩与经常上网有关.
学习成绩 上网 合计
经常 不经常 不及格 80 120 200
及格 120 680 800
合计 200 800 1 000
典型例题
PART.03
2×2列联表与等高堆积条形图
例1:下面是一个2×2列联表:
X Y 合计
Y=0 Y=1 X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为( )A.94,96 B.52,50 C.52,60 D.54,52
C
2×2列联表与等高堆积条形图
例2:已知两个分类变量X,Y,它们的取值分别为{x1,x2}和{y1,y2},观察下列各图,其中两个分类变量X,Y之间关系最强的是( )
D
课堂总结
PART.04
课堂总结
1.分类变量与数值变量;
2.2×2列联表;
3.等高堆积条形图。
4.2×2列联表与等高堆积条形图的实际应用。
统计学是对令人困惑费解的问题做出数字设想的艺术。
李思
THANK
