函数的应用[上学期]
图片预览



文档简介
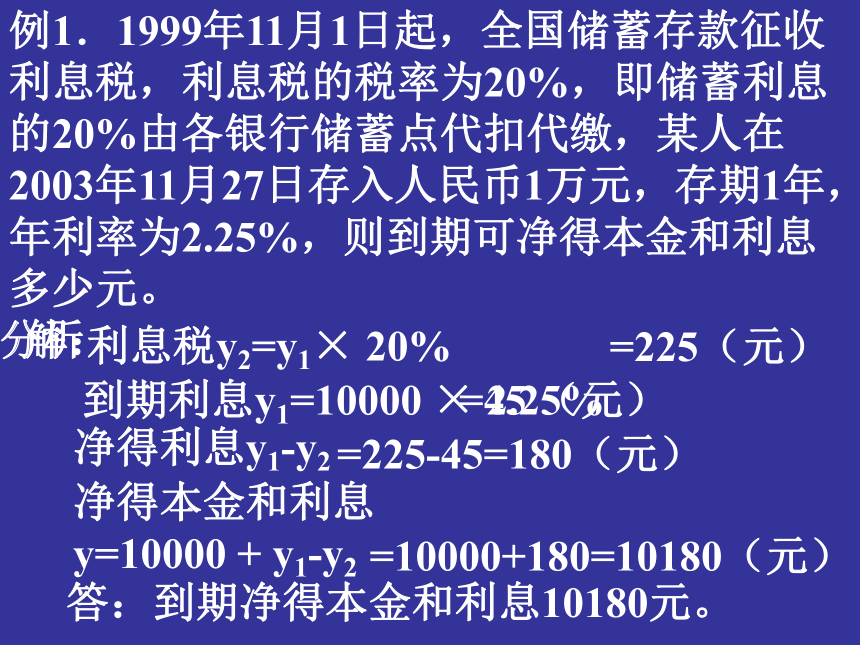
课件13张PPT。函数应用题孙广仁例1.1999年11月1日起,全国储蓄存款征收利息税,利息税的税率为20%,即储蓄利息的20%由各银行储蓄点代扣代缴,某人在2003年11月27日存入人民币1万元,存期1年,年利率为2.25%,则到期可净得本金和利息多少元。到期利息y1=10000 × 2.25%利息税y2=y1× 20%净得利息y1-y2净得本金和利息
y=10000 + y1-y2答:到期净得本金和利息10180元。=45 (元)=225-45=180(元)=225(元)=10000+180=10180(元)分析解:就是将数学结论转译成实际问题的结论。
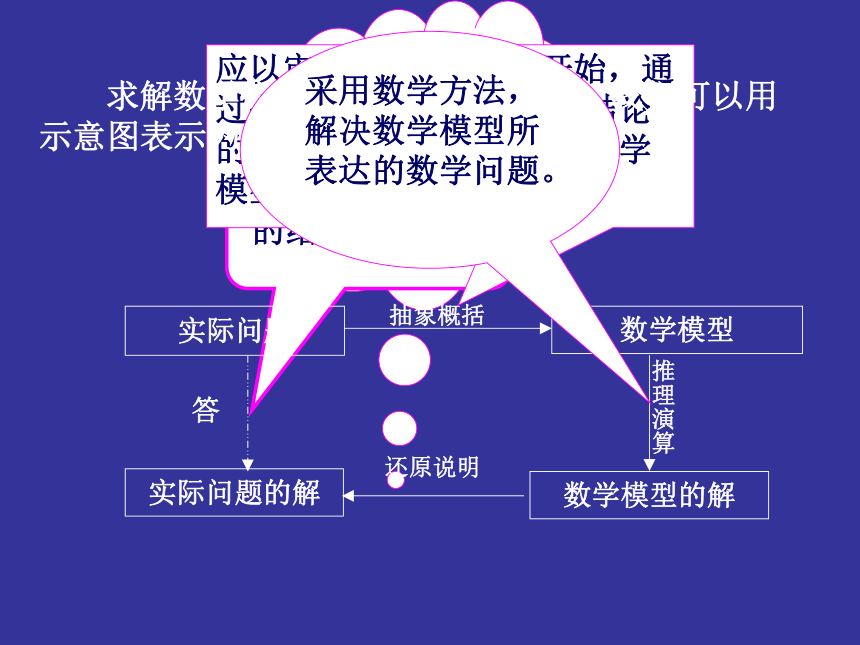
就是对实际问题的结论作出回答实际问题数学模型数学模型的解实际问题的解应以审题(即明确题意)开始,通过分析和抽象找出题设与结论的数学关系,建立合理的数学模型。
求解数学应用问题的思路和方法,我们可以用
示意图表示为:答采用数学方法,解决数学模型所表达的数学问题。
例2、某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲。【为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好。】若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
⑴把y表示成x的函数,并求出其定义域:
⑵试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?床位100x∈N *y=100x-575y=[100-3(x-10)]x-575 解:⑴答:该宾馆将床价定为22元时,既符合上面的两
个条件,又能使净收入高⑵ 当6≤x≤10且x∈N *时,
对于y=100x-575,
显然当x=10时,y有最大y值425元; 100x-575-3(x-65/3)2+2500/3y=6≤x≤10且x∈N*11≤x≤38且x∈N * 当11≤x≤38且x∈N *时,
对于y=-3(x-65/3)2+2500/3
y有最大值833元 。
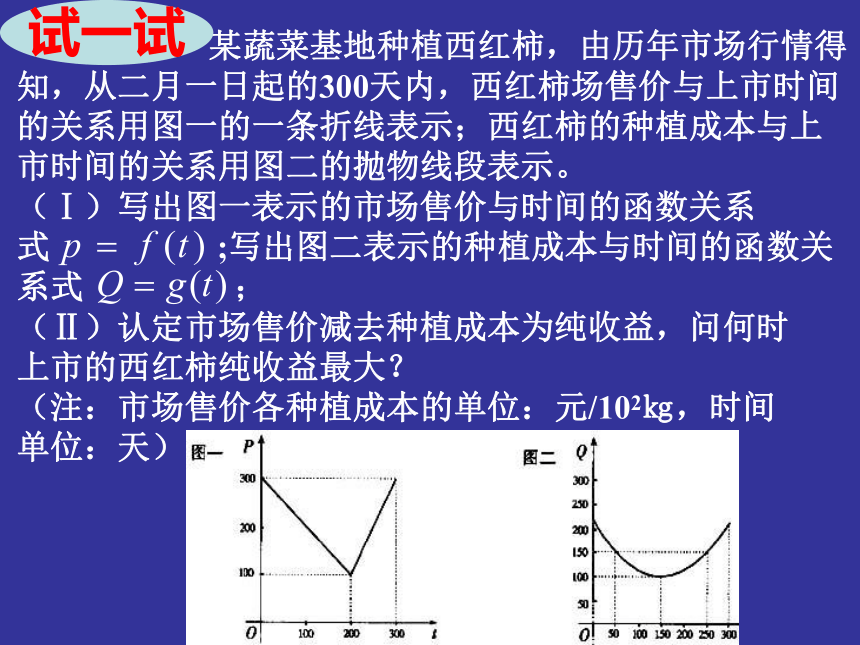
∴当x=22元时,y有最大y值833元 。 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
(Ⅰ)写出图一表示的市场售价与时间的函数关系式 ;写出图二表示的种植成本与时间的函数关系式 ;
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时
上市的西红柿纯收益最大?
(注:市场售价各种植成本的单位:元/102㎏,时间
单位:天)试一试解:(Ⅰ)由图一可得市场售价与时间的函数关系为由图二可得种植成本与时间的函数关系为(Ⅱ)设时刻的纯收益为h(t) , 则由题意得h(t)=f(t) -g(t)即 h(t)=∴当t=50时,h(t) 取得区间[0,200]上的最大值100; 当200<t≤300 时,配方整理得h(t)=∴当 t=300时, 取得区间(200,300]上的最大值87.5 综上,由100>87.5 可知,在区间[0,300]上可以
取得最大值100,此时 t=50 , 即从二月一日开始的第50天时,
上市的西红柿纯收益最大。 当 0≤t≤200 时,配方整理得h(t)=解:例4:如图:已知ABCD是边长为a的正方形,在AB,BC,CD,DA上分别取E,F,G,H使AE=BF=CG=DH=x,连结E,F,G,H得正方形EFGH,设其面积为S,求S关于x的函数,并问当E位于何处时,面积S最小,最小值是多少? ,EB=a-x,EF2=EB2+BF2演示趣味题某商品降价10%后,欲恢复原价,
则应提价多少???实际问题数学模型数学模型的解实际问题的解 求解数学应用问题的思路和方法,我们可以用
示意图表示为:答解应用问题的一般步骤:(1) 使实际问题数学化(2)用数学思想、方法解决数学问题(3)就是将数学结论转译成实际问题的结论。
(4)就是对实际问题的结论作出回答
作业 p89 1-3欢迎欢迎指导
y=10000 + y1-y2答:到期净得本金和利息10180元。=45 (元)=225-45=180(元)=225(元)=10000+180=10180(元)分析解:就是将数学结论转译成实际问题的结论。
就是对实际问题的结论作出回答实际问题数学模型数学模型的解实际问题的解应以审题(即明确题意)开始,通过分析和抽象找出题设与结论的数学关系,建立合理的数学模型。
求解数学应用问题的思路和方法,我们可以用
示意图表示为:答采用数学方法,解决数学模型所表达的数学问题。
例2、某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲。【为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好。】若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
⑴把y表示成x的函数,并求出其定义域:
⑵试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?床位100x∈N *y=100x-575y=[100-3(x-10)]x-575 解:⑴答:该宾馆将床价定为22元时,既符合上面的两
个条件,又能使净收入高⑵ 当6≤x≤10且x∈N *时,
对于y=100x-575,
显然当x=10时,y有最大y值425元; 100x-575-3(x-65/3)2+2500/3y=6≤x≤10且x∈N*11≤x≤38且x∈N * 当11≤x≤38且x∈N *时,
对于y=-3(x-65/3)2+2500/3
y有最大值833元 。
∴当x=22元时,y有最大y值833元 。 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
(Ⅰ)写出图一表示的市场售价与时间的函数关系式 ;写出图二表示的种植成本与时间的函数关系式 ;
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时
上市的西红柿纯收益最大?
(注:市场售价各种植成本的单位:元/102㎏,时间
单位:天)试一试解:(Ⅰ)由图一可得市场售价与时间的函数关系为由图二可得种植成本与时间的函数关系为(Ⅱ)设时刻的纯收益为h(t) , 则由题意得h(t)=f(t) -g(t)即 h(t)=∴当t=50时,h(t) 取得区间[0,200]上的最大值100; 当200<t≤300 时,配方整理得h(t)=∴当 t=300时, 取得区间(200,300]上的最大值87.5 综上,由100>87.5 可知,在区间[0,300]上可以
取得最大值100,此时 t=50 , 即从二月一日开始的第50天时,
上市的西红柿纯收益最大。 当 0≤t≤200 时,配方整理得h(t)=解:例4:如图:已知ABCD是边长为a的正方形,在AB,BC,CD,DA上分别取E,F,G,H使AE=BF=CG=DH=x,连结E,F,G,H得正方形EFGH,设其面积为S,求S关于x的函数,并问当E位于何处时,面积S最小,最小值是多少? ,EB=a-x,EF2=EB2+BF2演示趣味题某商品降价10%后,欲恢复原价,
则应提价多少???实际问题数学模型数学模型的解实际问题的解 求解数学应用问题的思路和方法,我们可以用
示意图表示为:答解应用问题的一般步骤:(1) 使实际问题数学化(2)用数学思想、方法解决数学问题(3)就是将数学结论转译成实际问题的结论。
(4)就是对实际问题的结论作出回答
作业 p89 1-3欢迎欢迎指导
