05高三数学压轴试题[上学期]

05高三数学压轴试题（一）
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的4个选项中，只有一项是符合题目要求的.
1.已知U为全集，若集合A、B、C满足A∩B=A∩C，则可以推出( )
A． B=C B．A∪B=A∪C C．A∪(B)=A∪(C) D．(A)∪B=(A)∪C
2.对总数为N的一批零件,抽取一个容量为40的样本，若每个零件被抽取的概率为，
则N的值为（ ）
A． 200 B．150 C．120 D．100
3．设a=()x，b=()x－1，c=，若x>1，则a，b，c的大小关系是（ ）
A． a4．设=，=，=，当=λ+μ(λ,μ∈R),且λ+μ=1时，点C在（ ）
A． 线段AB上 B．直线AB上 C．直线AB上,但除去点A D． 直线AB上,但除去点B
5．从17个相异的元素中选出2a－1个不同元素的选法记为P，从17个相异的元素中选出2a个不同元素的选法记为Q，从18个相异的元素中选出12个不同元素的选法记为S，若P+Q=S，则a的值为（ ）
A． 6 B． 6或8 C．3 D．3或6
6．若一个平面与正方体的12条棱所成的角均为θ，那么cosθ等于（ ）
A． B． C． D．
7．二项式(－x)n展开式中含有x4项，则n的可能取值是（ ）
A．5 B．6 C．3 D．7
8．已知函数(x)=，则–1(3)=( )
A．10 B． C． D． －
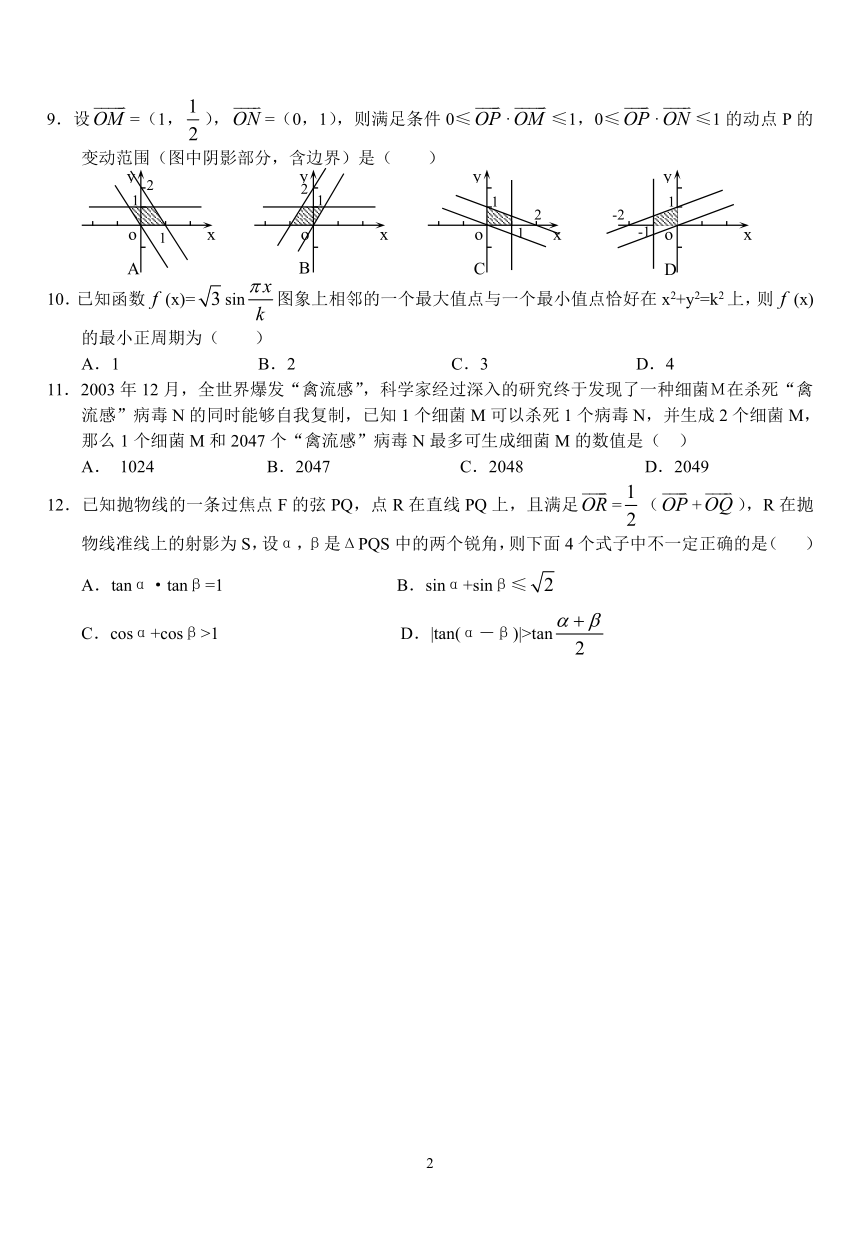
9．设=（1，），=（0，1），则满足条件0≤·≤1，0≤·≤1的动点P的变动范围（图中阴影部分，含边界）是（ ）
10．已知函数(x)=sin图象上相邻的一个最大值点与一个最小值点恰好在x2+y2=k2上，则(x)的最小正周期为（ ）
A．1 B．2 C．3 D．4
11．2003年12月，全世界爆发“禽流感”，科学家经过深入的研究终于发现了一种细菌Ｍ在杀死“禽流感”病毒N的同时能够自我复制，已知1个细菌M可以杀死1个病毒N，并生成2个细菌M，那么1个细菌M和2047个“禽流感”病毒N最多可生成细菌M的数值是（ ）
A． 1024 B．2047 C．2048 D．2049
12．已知抛物线的一条过焦点F的弦PQ，点R在直线PQ上，且满足=（+），R在抛物线准线上的射影为S，设α，β是ΔPQS中的两个锐角，则下面4个式子中不一定正确的是（ ）
A．tanα·tanβ=1 B．sinα+sinβ≤
C．cosα+cosβ>1 D．|tan(α－β)|>tan
05高三数学压轴试题（一）
班级：________ 姓名：________学号：_____
第Ⅱ卷（选择题 共90分）
二、填空题 本大题共4小题，每小题4分，共16分.
13．把函数的图象，按向量 （m>0）平移后所得的图象关于轴对称，则m的最小正值为__________________.
14．若关于x的不等式2－>|x－a| 至少有一个负数解，则a的取值范围为__________________．
15．利用函数(t)=12+3sin[(t－81)]可用来估计某一天的白昼时间的长短，其中(t)表示白昼的小时数，t是某天的序号，t=0表示1月1日，依此类推0≤t≤365，若二月份28天，则这一地区一年中白昼最长的大约是 月 日．
16．对于正整数a和大于2的正整数n，记aK=a－3(k－1).(k=1,2,3…n),S(a,n)=a1+a2+…+an,
写出|S(a,n)|≤2的2整数组：(1) (2) ．
三、解答题：本大题6个小题，共74分
17．（本小题满12分）已知A、B是ΔABC的两个内角，＝，
其中为互相垂直的单位向量，若.
(Ⅰ) 试问tanA·tanB是否为定值 若为定值，请求出；否则请说明理由；
(Ⅱ) 求tanC的最大值，并判断此时三角形的形状．
18. (本小题12分)设数列{an}的前项和为Sn，已知a1=1，Sn=nan﹣2n(n﹣1)，(n∈N*)
(Ⅰ)求证数列{an}为等差数列，并写出通项公式；
(Ⅱ)是否存在自然数，使得 若存在，求出n的值；
若不存在，说明理由；
19.（本小题满分12分）甲、乙两人进行乒乓球比赛，在每一局比赛中，甲获胜的概率为P．
（Ⅰ）如果甲、乙两人共比赛4局，甲恰好负2局的概率不大于其恰好胜3局的概率，试求P
的取值范围；
（Ⅱ）如果P=，当采用3局2胜制的比赛规则时，求甲获胜的概率.
20. （本小题满分12分）如图，在直角三角形ABC中，AD是斜边BC上的高，有很多大家熟悉的性质，例如“AB⊥AC”，勾股定理“|AB|2+|AC|2=|BC|2”和“=+”由此联想，在三棱锥O-ABC中，若三条侧棱OA，OB，OC两两互相垂直，可以推出那些结论？写出你的结论.（本题推出一个正确的结论给4分，满分不超过12分，文科只要求写出结论便可，理科要求给出必要的推理证明）
21. （本小题满分12分）
已知点Q位于直线右侧，且到点与到直线的距离之和等于4.
(Ⅰ) 求动点Q的轨迹C；
(Ⅱ) 直线过点交曲线C于A、B两点，点P满足，，又=(,0)，其中O为坐标原点，求的取值范围；
(Ⅲ) 在(Ⅱ)的条件下，能否成为以EF为底的等腰三角形？若能，求出此时直线的方程；
若不能，请说明理由．
22．（本小题满分14分）已知函数(x)满足(x+y)= (x)·(y)且(1)=．
(Ⅰ)当n∈N+时，求(n)的表达式；
(Ⅱ)设an=n·(n),n∈N+，求证a1+a2+…+an<2．
参 考 答 案
1．D 由A∩B=A∩C知B，C在A内部的元素相同，由韦恩图可得．
2．由题意= ∴N=120．
3．C 法一：取特殊值
法二：01,c=x<0即可
4．B ∵n+μ=1 ∴λ=1－μ，∵=λ+μ=+μ(－)=+μ
∴=－=μ，即与共线．
5． D 法一：反代法.分别取a=6，8代入验证。
法二：由题意可知+=即= ∴2a=12或2a=6. ∴a=6或a=3.
6． A 设正方体ABCD—A1B1C1D1的棱长为a,则平面AB1C与正方体的12条棱所成的角都相等，
ΔAB1C的中心为O，则AO=×sin60°×AC=a ∴cosθ=．
7．C 展开式的通项为()n-r·(－x)r=(－1)r·（r=0,1,2,…n）即存在自然数r，
使r－(n－1) =4即7r=3n+12且n≥r,故选C.
8．Ｃ ==x+3 依题意 当x>1时 f(x)>4
当x≤1时 f(x)=3x+1≤4 令t= f -1(3) ∴f(t)=3<4 即3t+1=3 ∴t=
9．A设点P(x,y) 则 0≤(x,y)·(1,)≤1 0≤(x,y)·(0,1)≤1 即0≤x+y≤1 0≤y≤1
因此动点P的变化范围是A中的阴影部分.
10．D 由题意得 = ∴x= , f(x)mox= 代入圆方程 ∴
∴f(x)= sin ∴ T=4．
11．C ∵1+2+22+…+2n=2n+1－1又2047=211－1∴n=10故最多生成细菌M的个数2×210=2048
12．D 解法（一）：由特殊情况，即PQ为通径的时候可以验证只有D不正确.
解法（二）：=(+) ∴点P是弦PQ的中点，设点P，Q在抛物线准线上的射影分别为， ,则|PF|=|P|，|QF|=|Q| ∴|RS|= (|PF|+|QF|)=|PQ|=|PR|=|QR| 则∠PSQ=90°
∴α+β=90°,故只有D不正确.
二、填空题
13． 解答： ＝ 由
得 ∴ ∴ ∴最小正值
14．
解答：数形结合法，分别作出y1=2－x2和
y2=|x |的图像，如图一
而y=|x－a|的图像可以由y2=|x |的图像经过
左右移动得到．图二就是移动后的两个端点
情况．
图二中，右侧的过点（0，2）可得a=2
左侧的为相切，由联立可得，a=
15． 6月22日 解答：当且仅当(t－81)= 即 t=172
∵t∈N且f(172)=12+3sin,f(173) =12+3sin ∴f(172)>f(173)即t=172时，f(t)最大，而172=30×5+22=31+28+31+30+31+21 ∴为6月22日．
16． 1) (3,3) (2) (4,4)
答：|na－3|≤2 ∴(n－1)≤a≤(n－1)+ 取n=3 则a=3;取n=4, 则a=4．
三、解答题
17．解答：(Ⅰ)||2= ∴ 即
∴ ∴
∴ ∴为定值.
(Ⅱ)==
≤
∴= 当且仅当 即 取得最大值，
此时ΔABC为等腰钝角三角形.(只答等腰三角形不扣分)
18.解答：(Ⅰ)当时，，
得，所以为等差数列，且
(Ⅱ) 假设存在满足条件的自然数n，则
∴ 所以，
由，得
19．解答：设每一局比赛中甲获胜为事件A，则P(A)＝P，0≤P≤1．
(Ⅰ)在n局比赛中甲胜k局，相当于事件A独立重复试验n次发生k次．
由题意， ∴
∴为所求.
(Ⅱ)设“比赛2局，甲全胜”为事件A，“比赛3局，前2局中甲胜1局，第3局甲胜”为事件B，则“采用3局2胜制比赛规则，甲获胜”为事件A+B,
故P(A+B)=P(A)+P(B)= 为所求.
20． 解答：可以得出以下结论：
（Ⅰ）三个侧面OAB、OAC、OBC两两互相垂直（或OA⊥BC、OB⊥AC、OC⊥AB）
（Ⅱ）O在底面的射影为底面ΔABC的重心H
（Ⅲ）=++（H为ΔABC的重心）
（Ⅳ）ΔABC一定是锐角三角形
（Ⅴ）++=
（Ⅵ）cos2α+ cos2β+cos2r=1 (α,β,Υ是三个侧面与底面ABC所成的角)
以下给出具体的证明：
(Ⅰ)证明：∵OA⊥OC,OB⊥OC ∴OC⊥平面OAB
∴平面OAC⊥平面OAB 平面OBC⊥平面OAB 同理可证平面OBC⊥平面OAＣ
(Ⅱ)证明：如图一，作AD⊥BC于D,BE⊥AC于E.
AD与BE交于H为垂心，连接OD
由(Ⅰ)中的证明可知OA⊥面OBC ∴OA⊥BC
又AD⊥BC ∴BC⊥平面OAD ∴BC⊥OH
同理可证AC⊥OH ∴OH⊥平面ABC
即H为O在平面ABC上的射影
∴O在ΔABC上的射影为ΔABC的垂心
（Ⅲ）证明：如图二 连接AH并延长AH交BC于D连接OD
∵OA⊥面OBC∴OA⊥OD
在RtΔABC中 ∵OH⊥OD ∴OH·AD=AO·OD
∴OH2·AD2=AO2·OD2
又∵AD2= OA2+ OD2 ∴=+
∵AD⊥BC，由三垂线定理得：BC⊥OD
∴在RtΔOBC中 OD2 ·BC2 =BO2·CO2
∴OD2= 又∵BC2= BO2+CO2
∴=+ ② 由①②得:=++
(Ⅳ) 证明：证明：设OA=a,OB=b,OC=c, 在RtΔOAB中，AB2= a2 + b2
在RtΔOBC中，BC2=b2+a2 在RtΔOAC中，AC2= a2 + a2 在ΔABC中，
由余弦定理可知cosA==
=>0 ∴0°<∠A<90° ∴∠A是锐角
同理可得∠B，∠C也为锐角，即ΔABC为锐角三角形
（Ⅴ）证明：如图二（延用（Ⅸ）中的字母a,b,c）∵H为垂心 ∴AD⊥BC
又∵OA、OB、OC两两垂直 ∴SΔOAB=ab SΔOBC=bc SΔOAC=ac SΔABC= BC·AD
∴++=( a2 b2+ b2 c2+ a2 c2)= a2(b2+ c2)+b2 c2…………①
又∵在RtΔBOC中,OD⊥BC ∴OB2·OC2= b2 c2=OD2·BC2=OD2·（b2+ c2）…………②
∴②代入①得：++=（b2+ c2）·AD2=BC2·AD2=
（Ⅵ）证明：如图二: （延用（Ⅸ）中的字母a,b,c）∵OD⊥BC AD⊥BC
∴∠ODA即二面角O—BC—A的平面角 令∠ODA=α ∴cosα=
在RtΔOBC中OD= 在RtΔCAD中AD==
∴cosα== 同理：cosβ=
cos r= ∴cos2α+ cos2β+ cos2 r=1
21．（本小题14分）解：（Ⅰ）设，则，即：
，化简得：．
所以，动点Q的轨迹为抛物线位于直线右侧的部分．
（Ⅱ）因为，所以，P为AB中点；又因为，且=(,0)，
所以，点E为线段AB垂直平分线与x轴焦点．
由题可知：直线与轴不垂直，所以可设直线的方程为，
代入轨迹C的方程得到： （＊）
设，要使得与C有两个不同交点，需且只需
解之得：．
由（＊）式得：，所以，AB中点P的坐标为：
，．所以，直线EP的方程为
令得到点E的横坐标为．因为，所以，∈（，－3）．
（Ⅲ）不可能．要使成为以EF为底的等腰三角形，需且只需，
即：，解得：．
另一方面，要使直线满足（2）的条件，需要，
所以，不可能使成为以EF为底的等腰三角形．
22．（Ⅰ）由f(x+y)=f(x)·f(y)得 f(n+1)=f(n)·f(1)=f(n),(n∈N+).
∴数列｛f(n)｝是以f(1)= 为首项，是以 为公比的等比数列 ∴f(n)=
(Ⅱ)an=n·f(n)=n 令S=a1+a2+…+an.
∴S=+2·+3·+…+(n－1)·+n·……………………①
S=+2·+3·+…+(n－1)·+n·………………②
①－② 得：S＝+++…++ －n·
∴Ｓ＝－n·＝２――n·＜２．
y
o
x
x
y
o
x
y
o
x
y
o
1
1
2
2
1
1
1
2
-2
1
-1
B
A
C
D
D
A
B
C
图一
O
A
B
C
H
E
D
C
图二
B
A
H
E
D
C
A
O
O
B
y1=2－x2
y2=|x|
图一
２
ｙ
ｘ
ｘ
ｙ
２
图二
y2=|x－a|
y1=2－x2
11