6.7 用相似三角形解决问题 同步练习(无答案)苏科版九年级数学下册
文档属性
| 名称 | 6.7 用相似三角形解决问题 同步练习(无答案)苏科版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 00:08:13 | ||
图片预览


文档简介
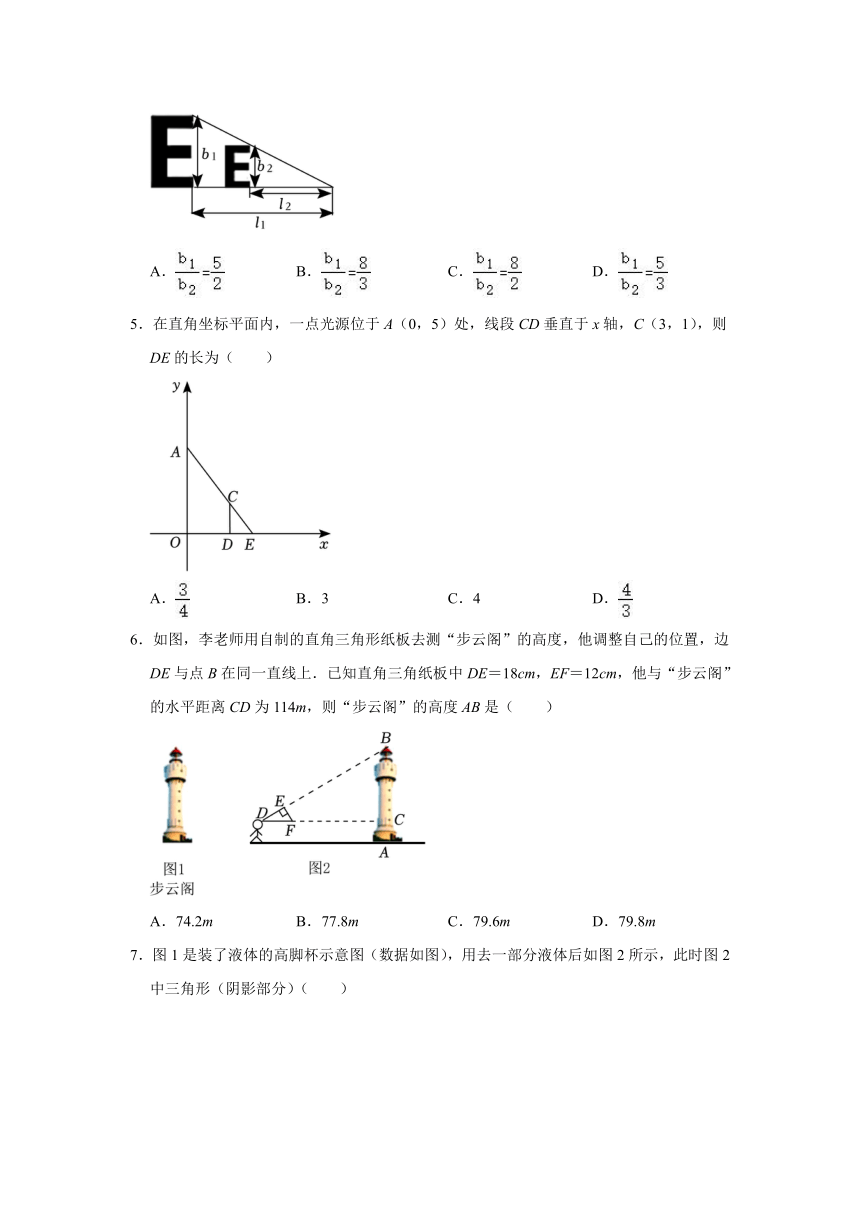
6.7 用相似三角形解决问题(练习)-苏科版九年级下册
一.选择题
1.凸透镜成像的原理如图所示,AD∥l∥BC.若物体到焦点的距离与焦点到凸透镜中心线DB的距离之比为5:4,则物体被缩小到原来的( )
A. B. C. D.
2.如图,梯子AB斜靠在墙上,梯子底端离墙脚的距离BC=1.2m,则梯子AB的长为( )
A.2m B.2.4m C.3m D.3.6m
3.如图,线段AB,EF,竹竿,楼房的高度,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,竹竿的高度为3m,则楼房的高度是( )
A.25m B.26.5m C.50m D.51.5m
4.视力表对我们来说并不陌生,如图,现需制作标准视力表1=5米,此时字母E的高度为b1米.由于场地有限,需要缩小测试距离为l2=3米,修改后视力表字母E的高度为b2米,则b1与b2的关系为( )
A. B. C. D.
5.在直角坐标平面内,一点光源位于A(0,5)处,线段CD垂直于x轴,C(3,1),则DE的长为( )
A. B.3 C.4 D.
6.如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整自己的位置,边DE与点B在同一直线上.已知直角三角纸板中DE=18cm,EF=12cm,他与“步云阁”的水平距离CD为114m,则“步云阁”的高度AB是( )
A.74.2m B.77.8m C.79.6m D.79.8m
7.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时图2中三角形(阴影部分)( )
A.5cm2 B.6cm2 C.7cm2 D.8cm2
8.如图,在A时测得一棵大树的影长为4米,B时又测得该树的影长为9米,则树的高度是( )
A.4 B.6 C.8 D.9
9.有一块锐角三角形余料△ABC,边BC的长为20cm,BC边上的高为l6cm,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为5cm的边在BC上( )
A.5个 B.6个 C.7个 D.8个
10.如图,有一张锐角三角形纸片,边BC=3,要把它加工成正方形纸片,使其一边在BC上,AC上,则这个正方形EFGH纸片的周长为( )
A.1 B.1.2 C.4.8 D.5
二.填空题
.如图①,西周数学家商高用“矩”测量物高的方法:把矩的两边放置成如图②的位置,从矩的一端A(人眼),使视线通过点C,记人站立的位置为点B,即可算得物高EG.经测量,得CD=60cm,AB=1.5m.设BG=x(m),EG=y(m) .
.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,问:邑方几何?”.其大意是:如图,一座正方形城池,从点A往正北方向走30步到B处有一树木,C为西门中点,设正方形城池的边长为x步.根据题意整理成一元二次方程的一般形式 .
.甲、乙两幢完全一样的房子如图1,小聪与弟弟住在甲幢,为测量对面的乙幢屋顶斜坡M,制定如下方案:两幢房子截面图如图2,AB=12m(平面镜的大小忽略不计),弟弟在离点G水平距离3m的点H处恰好在镜子中看到乙幢屋顶N,此时测得弟弟眼睛与镜面的竖直距离IH=0.6m.下楼后,测得地面点F与E,M,N在一条直线上,FD=2m,BF=5m m,乙幢屋顶斜坡M,N之间的距离为 m.
.如图,某学生利用一根长1米的标杆EC测量一棵树的高度,测得BC=3米,那么树的高度DB为 .
.如图,数学实践课上,老师布置任务如下:让小明(AB)(CD),所用工具为一个平面镜P和必要的长度测量工具(点B,P,D在同一条直线上).已知小明眼睛距地面1.6m,当小明与平面镜相距 m时,恰好能从平面镜里观测到大树的顶端.
三.解答题
.如图,在△ABC中,∠C=90°,BC=8,动点D、E分别在边BA、BC上,且,与直线DE相交于点F.
(1)当DB=DE时,求t的值;
(2)当t=时,求的值;
(3)当△BDE与△BDF相似时,求BF的长.
.如图,在Rt△ABC中,∠BAC=90°,以A为圆心,AE为半径作⊙A交BE于点F,AF的延长线交BC于点D,作EK⊥BC
(1)求证:AD⊥BC;
(2)求证:;
(3)当BF BE=BG BH且AH=BD时,求证:.
.如图①,在△ABC中,∠ACB=90°,点E、F分别是边BC,AC上的点
(1)尝试探究:请直接填空
①的值为 ;
②直线AF与直线BE的位置关系为 ;
(2)类比延伸:如图②,若将图①中的△CEF绕点C顺时针旋转,连接AF,则在旋转的过程中,请判断,并说明理由;
(3)拓展运用:若BC=3,CE=2,在旋转过程中,E,F三点在同一直线上时,请直接写出此时线段AF的长.
.如图1.在△ABC中,∠ABC=120°,AB=BC=1.
(1)求AC长.
(2)如图2,若点D是AC上一动点(不与A、C重合),在BC上取一点E
①求证:△ABD∽△CDE.
②设AD=x,BE=y,求y关于x的函数表达式及自变量x的取值范围,BE的值最小?
.如图①,“丝绸之路群雕”刻画和表达了一队来往于丝路中途的中外混合的骆驼商旅,已成为西安著名的城市标志之一.为了测量群雕某处的高度AB,首先,小明在M处放置了一面平面镜,当小明蹲在点D处时恰好能在平面镜中看到雕塑顶端A的像,此时小明的眼睛到地面的距离CD=0.7米;然后小明在D处起立站直,晓璐眼睛贴地观察发现地面上点F、小明头顶E和顶端A重合,DF=1.5米,AB⊥BF,点B、M、D、F在同一条水平线上,点C在DE上(平面镜的大小、厚度忽略不计,晓璐眼睛贴地观察时眼睛到地面的距离忽略不计)
一.选择题
1.凸透镜成像的原理如图所示,AD∥l∥BC.若物体到焦点的距离与焦点到凸透镜中心线DB的距离之比为5:4,则物体被缩小到原来的( )
A. B. C. D.
2.如图,梯子AB斜靠在墙上,梯子底端离墙脚的距离BC=1.2m,则梯子AB的长为( )
A.2m B.2.4m C.3m D.3.6m
3.如图,线段AB,EF,竹竿,楼房的高度,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,竹竿的高度为3m,则楼房的高度是( )
A.25m B.26.5m C.50m D.51.5m
4.视力表对我们来说并不陌生,如图,现需制作标准视力表1=5米,此时字母E的高度为b1米.由于场地有限,需要缩小测试距离为l2=3米,修改后视力表字母E的高度为b2米,则b1与b2的关系为( )
A. B. C. D.
5.在直角坐标平面内,一点光源位于A(0,5)处,线段CD垂直于x轴,C(3,1),则DE的长为( )
A. B.3 C.4 D.
6.如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整自己的位置,边DE与点B在同一直线上.已知直角三角纸板中DE=18cm,EF=12cm,他与“步云阁”的水平距离CD为114m,则“步云阁”的高度AB是( )
A.74.2m B.77.8m C.79.6m D.79.8m
7.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时图2中三角形(阴影部分)( )
A.5cm2 B.6cm2 C.7cm2 D.8cm2
8.如图,在A时测得一棵大树的影长为4米,B时又测得该树的影长为9米,则树的高度是( )
A.4 B.6 C.8 D.9
9.有一块锐角三角形余料△ABC,边BC的长为20cm,BC边上的高为l6cm,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为5cm的边在BC上( )
A.5个 B.6个 C.7个 D.8个
10.如图,有一张锐角三角形纸片,边BC=3,要把它加工成正方形纸片,使其一边在BC上,AC上,则这个正方形EFGH纸片的周长为( )
A.1 B.1.2 C.4.8 D.5
二.填空题
.如图①,西周数学家商高用“矩”测量物高的方法:把矩的两边放置成如图②的位置,从矩的一端A(人眼),使视线通过点C,记人站立的位置为点B,即可算得物高EG.经测量,得CD=60cm,AB=1.5m.设BG=x(m),EG=y(m) .
.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,问:邑方几何?”.其大意是:如图,一座正方形城池,从点A往正北方向走30步到B处有一树木,C为西门中点,设正方形城池的边长为x步.根据题意整理成一元二次方程的一般形式 .
.甲、乙两幢完全一样的房子如图1,小聪与弟弟住在甲幢,为测量对面的乙幢屋顶斜坡M,制定如下方案:两幢房子截面图如图2,AB=12m(平面镜的大小忽略不计),弟弟在离点G水平距离3m的点H处恰好在镜子中看到乙幢屋顶N,此时测得弟弟眼睛与镜面的竖直距离IH=0.6m.下楼后,测得地面点F与E,M,N在一条直线上,FD=2m,BF=5m m,乙幢屋顶斜坡M,N之间的距离为 m.
.如图,某学生利用一根长1米的标杆EC测量一棵树的高度,测得BC=3米,那么树的高度DB为 .
.如图,数学实践课上,老师布置任务如下:让小明(AB)(CD),所用工具为一个平面镜P和必要的长度测量工具(点B,P,D在同一条直线上).已知小明眼睛距地面1.6m,当小明与平面镜相距 m时,恰好能从平面镜里观测到大树的顶端.
三.解答题
.如图,在△ABC中,∠C=90°,BC=8,动点D、E分别在边BA、BC上,且,与直线DE相交于点F.
(1)当DB=DE时,求t的值;
(2)当t=时,求的值;
(3)当△BDE与△BDF相似时,求BF的长.
.如图,在Rt△ABC中,∠BAC=90°,以A为圆心,AE为半径作⊙A交BE于点F,AF的延长线交BC于点D,作EK⊥BC
(1)求证:AD⊥BC;
(2)求证:;
(3)当BF BE=BG BH且AH=BD时,求证:.
.如图①,在△ABC中,∠ACB=90°,点E、F分别是边BC,AC上的点
(1)尝试探究:请直接填空
①的值为 ;
②直线AF与直线BE的位置关系为 ;
(2)类比延伸:如图②,若将图①中的△CEF绕点C顺时针旋转,连接AF,则在旋转的过程中,请判断,并说明理由;
(3)拓展运用:若BC=3,CE=2,在旋转过程中,E,F三点在同一直线上时,请直接写出此时线段AF的长.
.如图1.在△ABC中,∠ABC=120°,AB=BC=1.
(1)求AC长.
(2)如图2,若点D是AC上一动点(不与A、C重合),在BC上取一点E
①求证:△ABD∽△CDE.
②设AD=x,BE=y,求y关于x的函数表达式及自变量x的取值范围,BE的值最小?
.如图①,“丝绸之路群雕”刻画和表达了一队来往于丝路中途的中外混合的骆驼商旅,已成为西安著名的城市标志之一.为了测量群雕某处的高度AB,首先,小明在M处放置了一面平面镜,当小明蹲在点D处时恰好能在平面镜中看到雕塑顶端A的像,此时小明的眼睛到地面的距离CD=0.7米;然后小明在D处起立站直,晓璐眼睛贴地观察发现地面上点F、小明头顶E和顶端A重合,DF=1.5米,AB⊥BF,点B、M、D、F在同一条水平线上,点C在DE上(平面镜的大小、厚度忽略不计,晓璐眼睛贴地观察时眼睛到地面的距离忽略不计)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
