19.3.1正方形的定义与性质课件
文档属性
| 名称 | 19.3.1正方形的定义与性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 960.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-07 22:36:04 | ||
图片预览




文档简介
课件45张PPT。标题/完美的正方形
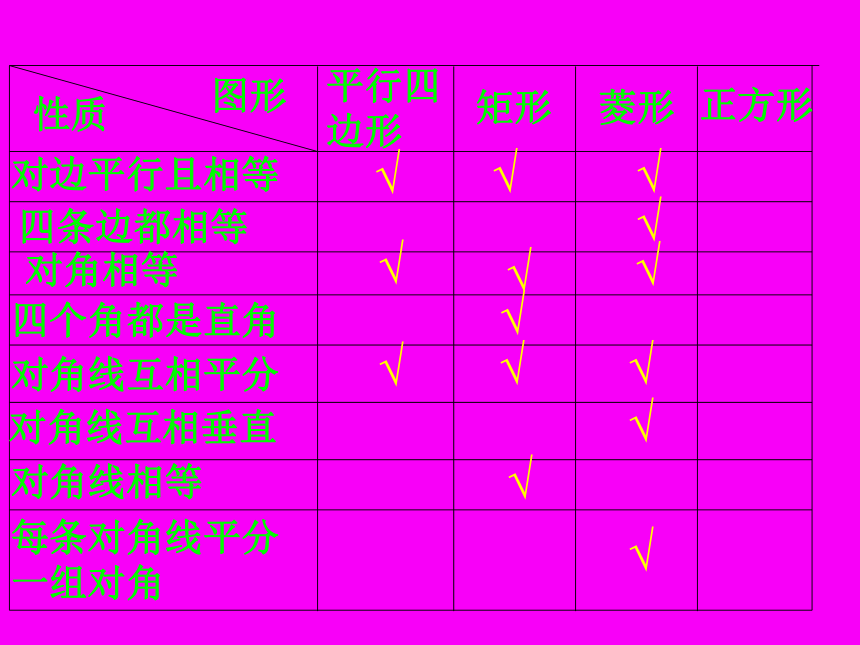
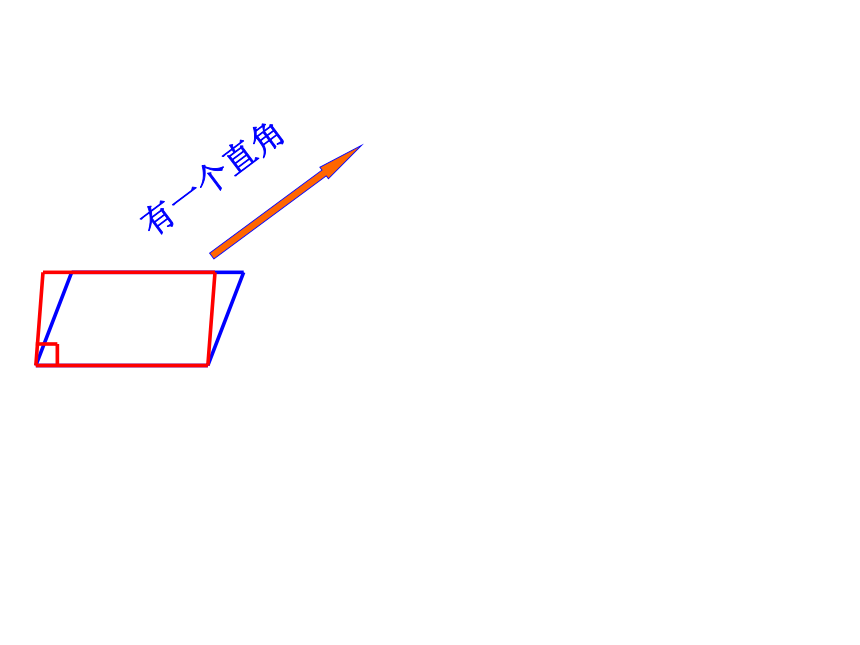
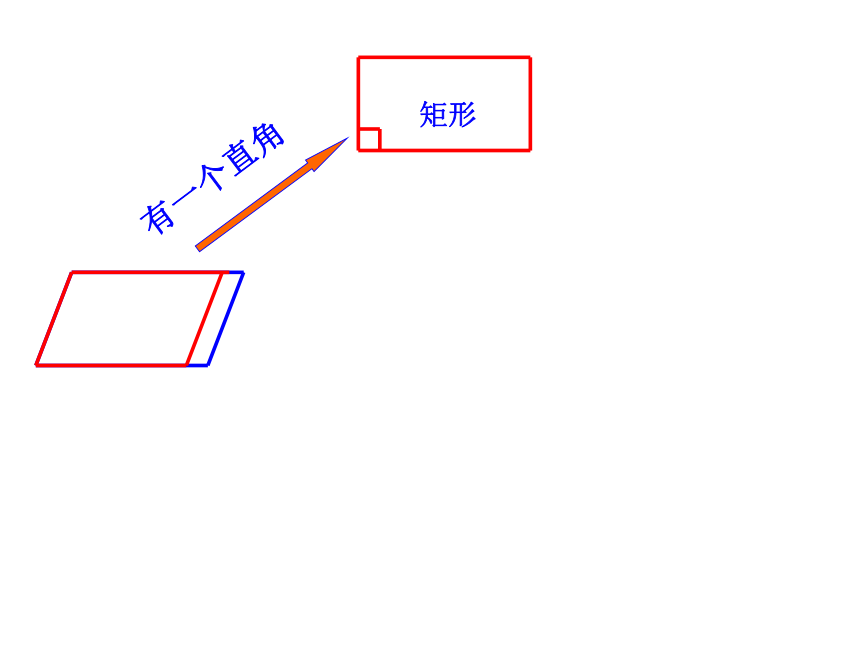
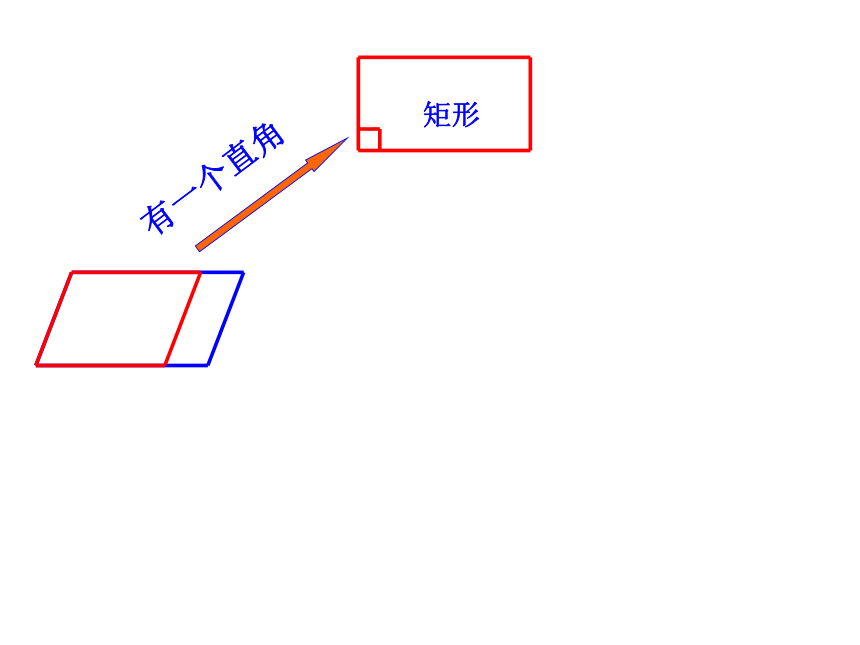
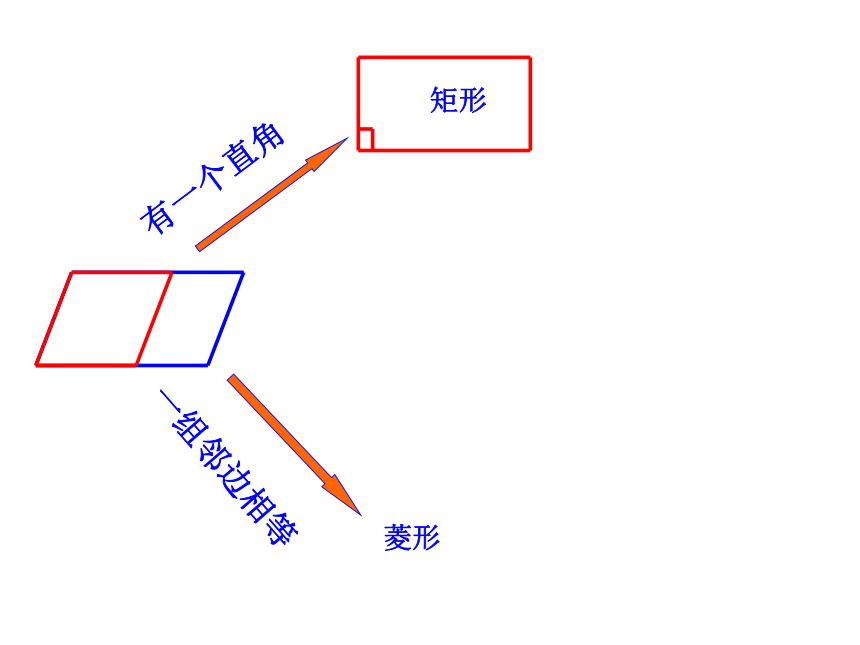
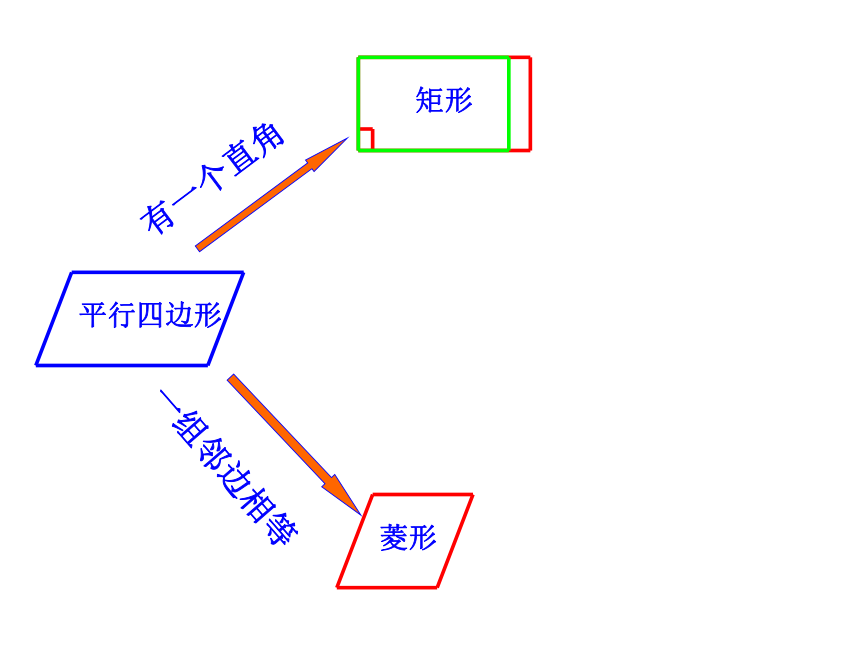
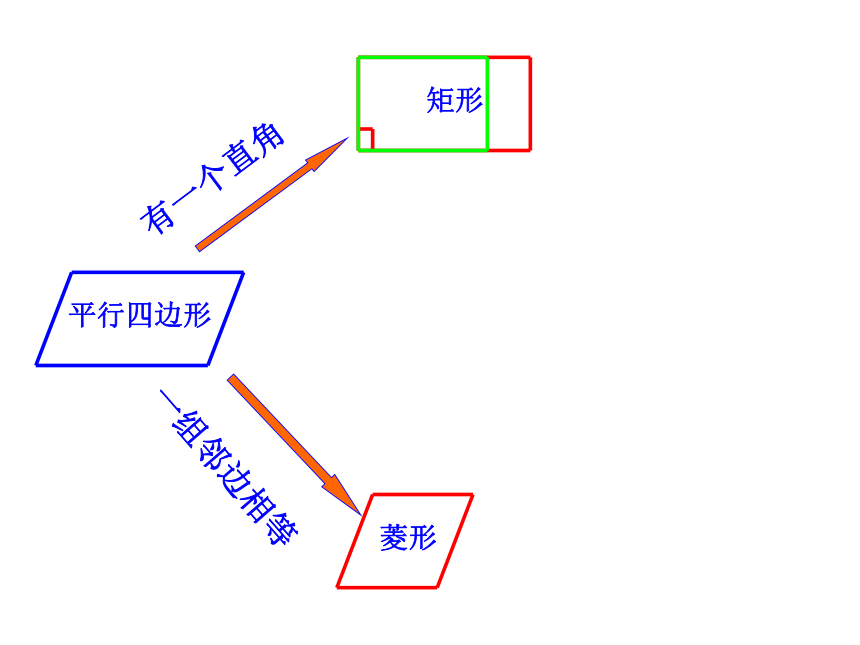
标题19.3.1 正方形学习目标 1、掌握正方形的定义和性质.2、经历正方形性质的探究过程.3、能利用正方形的性质解决问题.√√√√√√√√√√√√√√有一个直角有一个直角矩形有一个直角矩形有一个直角一组邻边相等矩形菱形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等有一个直角正方形平行四边形你能给正方形下一个定义吗?你能从这个变化过程中给正方形下定义吗?有一个角是直角的菱形叫做正方形。有一组邻边相等的矩形叫做正方形。有一个角是直角一组邻边相等的平行四边形叫做正方形。平行四边形矩形四边形菱形正
方
形四边形、平行四边形、矩形、菱形、正方形的关系为什么说正方形是个完美的图形?对称性特征正方形是中心对称图形它也是轴对称图形(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角对边平行,四条边都相等四个角都是直角边对角线角正方形的性质变换特征正方形是中心对称图形,
也是轴对称图形
周长面积边长×4边长×边长(对角线的平方÷2)例题解析例题例1. 如图,在正方形ABCD中,对角线AC、BD相交于O,
1)图中有多少个等腰直角三角形
2)说出图中相等的线段、相等的角。
3)求∠ABD、∠DAC、∠DOC的度数。课堂练习45°正方形12cm2a+11.正方形的一边和对角线的夹角为___________.2.如果一个四边形既是菱形又是矩形,那么它一定是_________.3.已知正方形的面积为9cm,它的周长为 _______________.4.正方形的边长为a,当边长增加1时,其面积增加了__________.正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选变式:正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD·2.从四边形内能找一点,使该点到各边距离都相等的
图形可能是 ( )
A.平行四边形、矩形、菱形 B.菱形、矩形 、正方形
C.矩形、正方形 D.菱形、正方形D3.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .8cm 4.已知正方形的一条对角线长为4cm,则它的边长
为 , 面积为 。例2 已知:如图,在正方形ABCD中,点 E在AC上.
求证:BE=DE证明:∵四边形ABCD 是正方形,
∴AB=AD, ∠BAC=∠DAC. 在△ABC和△ADC中
AB=AD
∠BAC=∠DAC.
AE=AE
∴△ABC≌△ADC (SAS)
∴BE=DE (全等三角形的对应边相等)例3 正方形ABCD中,E是BC延长线上一点,且CE=AC,
AE交DC于点F,试求∠E, ∠AFC的度数解:∵四边形ABCD为正方形,∵CE=AC∴∠E=∠CAE∵∠ACB是⊿ACE的一个外角∴∠ACB=∠E+∠CAE=2∠E∵∠AFC是△CEF的一个外角∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°∴∠E=22.5°, ∠AFC=112.5°jFEABDC练习:
1、如图,正方形ABCD中,BE=BD,
∠E= 30°2.以正方形ABCD的一边DC向外作等边△DCE,
则∠AEB=_____.4、正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.3.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.516cm分析:PE=AE,PF=OE
PE+PF=OA例4、如图,四边形ABCD是正方形,G是BC上
的一点,DE⊥AG于点E, BF⊥AG于点F,
求证(1)△ABF≌ △DAE
(2)DE=FE+FB练习:如图,E是正方形ABCD对角线AC上一
点,连结BE,AF⊥BE于点F,交BD于
点G,
证明:(1)AG=BE,AE=DG
(2)∠AGB= ∠BEC例5、如图,E是正方形ABCD内一点,如果
△ABE为等边三角形,求∠EDC的度数练习、如图,正方形ABCD中,对角线AC、BD
相交于点O,DE=CF,
求证:(1)OE=OF
(2)OE⊥OF例6、 已知:如图,四边形ABCD与四
边形DEFG都是正方形.
求证:AE=CG证明:∵四边形ABCD和DEFG都是正方形.
∴DA=DC, DE=DG ,∠ADC=∠EDG
(正方形四条边都相等,四个角都是直角)
∴∠ADC-∠ADG=∠EDG-∠ADG, 即∠GDC=∠EDA在△GDC和△EDA中
DC=DA
∠GDC=∠EDA.
DG=DE
∴△GDC≌△EDA (SAS)
∴AE=CG (全等三角形的对应边相等)例7、如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF练习.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 练习.如图,在AB上取一点C,以AC、BC为正
方形的一边在同一侧作正方形AEDC和
BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
例8.如图(3),正方形ABCD中,AC、BD相交于O, 分析:要证明BM=CN,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
AB=BC,∠1=∠2=45 ° AM=BN△ABM≌△BCN正方形ABCDOM=ON∠OMN=∠ONM=45°练习、正方形ABCD中∠DAF=25°,AF交对
角线BD于E,交CD于F,求∠ BEC的度数.ABCDEF思考活动与探索如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450G变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。 自主学习 随堂练习用10米长的篱笆围成一个四边形菜地,应如
何确定面积最大的四边形的形状?问题: 由三条公路围成的一个区域为直角三角形形状.工程队要想在区域内划一块正方形的地块作为新小区,且让小区足够大,请你来帮工程队设计一下 学以致用ABCDEF┓┓┓小结反思
标题19.3.1 正方形学习目标 1、掌握正方形的定义和性质.2、经历正方形性质的探究过程.3、能利用正方形的性质解决问题.√√√√√√√√√√√√√√有一个直角有一个直角矩形有一个直角矩形有一个直角一组邻边相等矩形菱形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等有一个直角正方形平行四边形你能给正方形下一个定义吗?你能从这个变化过程中给正方形下定义吗?有一个角是直角的菱形叫做正方形。有一组邻边相等的矩形叫做正方形。有一个角是直角一组邻边相等的平行四边形叫做正方形。平行四边形矩形四边形菱形正
方
形四边形、平行四边形、矩形、菱形、正方形的关系为什么说正方形是个完美的图形?对称性特征正方形是中心对称图形它也是轴对称图形(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角对边平行,四条边都相等四个角都是直角边对角线角正方形的性质变换特征正方形是中心对称图形,
也是轴对称图形
周长面积边长×4边长×边长(对角线的平方÷2)例题解析例题例1. 如图,在正方形ABCD中,对角线AC、BD相交于O,
1)图中有多少个等腰直角三角形
2)说出图中相等的线段、相等的角。
3)求∠ABD、∠DAC、∠DOC的度数。课堂练习45°正方形12cm2a+11.正方形的一边和对角线的夹角为___________.2.如果一个四边形既是菱形又是矩形,那么它一定是_________.3.已知正方形的面积为9cm,它的周长为 _______________.4.正方形的边长为a,当边长增加1时,其面积增加了__________.正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选变式:正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD·2.从四边形内能找一点,使该点到各边距离都相等的
图形可能是 ( )
A.平行四边形、矩形、菱形 B.菱形、矩形 、正方形
C.矩形、正方形 D.菱形、正方形D3.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .8cm 4.已知正方形的一条对角线长为4cm,则它的边长
为 , 面积为 。例2 已知:如图,在正方形ABCD中,点 E在AC上.
求证:BE=DE证明:∵四边形ABCD 是正方形,
∴AB=AD, ∠BAC=∠DAC. 在△ABC和△ADC中
AB=AD
∠BAC=∠DAC.
AE=AE
∴△ABC≌△ADC (SAS)
∴BE=DE (全等三角形的对应边相等)例3 正方形ABCD中,E是BC延长线上一点,且CE=AC,
AE交DC于点F,试求∠E, ∠AFC的度数解:∵四边形ABCD为正方形,∵CE=AC∴∠E=∠CAE∵∠ACB是⊿ACE的一个外角∴∠ACB=∠E+∠CAE=2∠E∵∠AFC是△CEF的一个外角∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°∴∠E=22.5°, ∠AFC=112.5°jFEABDC练习:
1、如图,正方形ABCD中,BE=BD,
∠E= 30°2.以正方形ABCD的一边DC向外作等边△DCE,
则∠AEB=_____.4、正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.3.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.516cm分析:PE=AE,PF=OE
PE+PF=OA例4、如图,四边形ABCD是正方形,G是BC上
的一点,DE⊥AG于点E, BF⊥AG于点F,
求证(1)△ABF≌ △DAE
(2)DE=FE+FB练习:如图,E是正方形ABCD对角线AC上一
点,连结BE,AF⊥BE于点F,交BD于
点G,
证明:(1)AG=BE,AE=DG
(2)∠AGB= ∠BEC例5、如图,E是正方形ABCD内一点,如果
△ABE为等边三角形,求∠EDC的度数练习、如图,正方形ABCD中,对角线AC、BD
相交于点O,DE=CF,
求证:(1)OE=OF
(2)OE⊥OF例6、 已知:如图,四边形ABCD与四
边形DEFG都是正方形.
求证:AE=CG证明:∵四边形ABCD和DEFG都是正方形.
∴DA=DC, DE=DG ,∠ADC=∠EDG
(正方形四条边都相等,四个角都是直角)
∴∠ADC-∠ADG=∠EDG-∠ADG, 即∠GDC=∠EDA在△GDC和△EDA中
DC=DA
∠GDC=∠EDA.
DG=DE
∴△GDC≌△EDA (SAS)
∴AE=CG (全等三角形的对应边相等)例7、如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF练习.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 练习.如图,在AB上取一点C,以AC、BC为正
方形的一边在同一侧作正方形AEDC和
BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
例8.如图(3),正方形ABCD中,AC、BD相交于O, 分析:要证明BM=CN,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
AB=BC,∠1=∠2=45 ° AM=BN△ABM≌△BCN正方形ABCDOM=ON∠OMN=∠ONM=45°练习、正方形ABCD中∠DAF=25°,AF交对
角线BD于E,交CD于F,求∠ BEC的度数.ABCDEF思考活动与探索如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450G变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。 自主学习 随堂练习用10米长的篱笆围成一个四边形菜地,应如
何确定面积最大的四边形的形状?问题: 由三条公路围成的一个区域为直角三角形形状.工程队要想在区域内划一块正方形的地块作为新小区,且让小区足够大,请你来帮工程队设计一下 学以致用ABCDEF┓┓┓小结反思
