人教版数学九年级下册28.2.2应用举例(2)——的仰角、俯角 教学设计
文档属性
| 名称 | 人教版数学九年级下册28.2.2应用举例(2)——的仰角、俯角 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 567.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 08:09:26 | ||
图片预览

文档简介
28.2.2应用举例(2)
教学目标:
能根据直角三角形的知识解决与仰角、俯角有关的实际问题。
教学重点:
将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决。
教学难点:
学会准确分析问题并将实际问题转化成数学模型。
教学过程:
一 复习回顾
在学习新课前,我们来进行一个课前热身:
如图,在△ABC中, ∠C=90°, ∠A 、∠B 、∠C的对边分别为a,b,c 。
(1)若已知∠A的度数和 a 的长度, 则c =______, b =______.
(2)若已知∠A的度数和 b 的长度, 则c=______,a =______.
(3)若已知∠A的度数为α和 c 的长度, 则a =_____,b =____.
设计意图:充分利用学生知识最近发展区进入主题。
二 引入新课
看来大家对基础知识掌握得还是比较牢固的。下面我们来看这样一个问题:
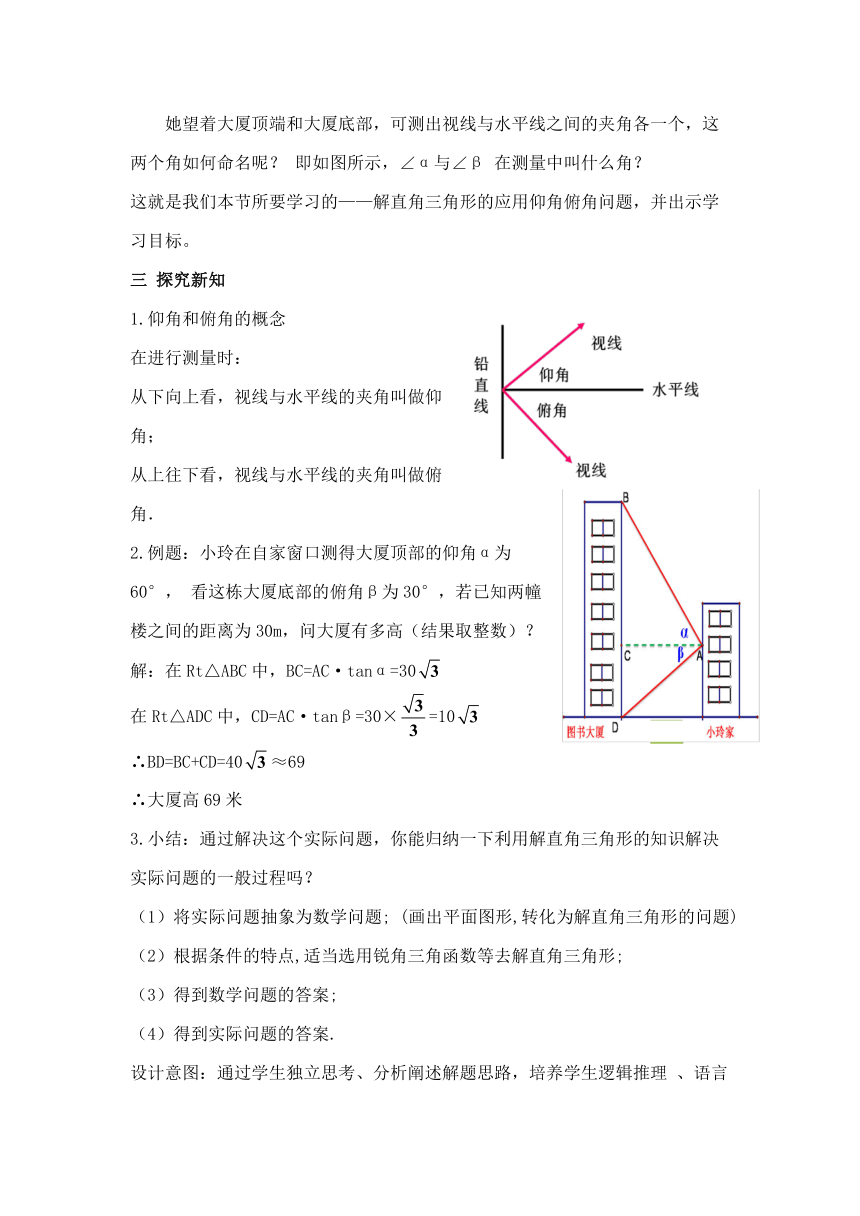
小玲家对面新造了一幢图书大厦,小玲站在自家 窗口,望着眼前的大厦心想:“这幢图书大厦到底有多高啊?能否用所学的数学知识计算楼高呢?”
她望着大厦顶端和大厦底部,可测出视线与水平线之间的夹角各一个,这两个角如何命名呢? 即如图所示,∠α与∠β 在测量中叫什么角?
这就是我们本节所要学习的——解直角三角形的应用仰角俯角问题,并出示学习目标。
三 探究新知
1.仰角和俯角的概念
在进行测量时:
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
2.例题:小玲在自家窗口测得大厦顶部的仰角α为60°, 看这栋大厦底部的俯角β为30°,若已知两幢楼之间的距离为30m,问大厦有多高(结果取整数)?
解:在Rt△ABC中,BC=AC·tanα=30
在Rt△ADC中,CD=AC·tanβ=30×=10
∴BD=BC+CD=40≈69
∴大厦高69米
3.小结:通过解决这个实际问题,你能归纳一下利用解直角三角形的知识解决实际问题的一般过程吗?
(1)将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题)
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
设计意图:通过学生独立思考、分析阐述解题思路,培养学生逻辑推理 、语言表达等能力,培养学生运用抽象、转化、化归思想将实际问题抽象转化为数学问题。通过选择不同的关系式解决此题对比讨论得出用锐角三角函数解直角三角形关键:正确选择关系式,及选择关系式原则:一选择的关系式尽量使用原始数据,二选择关系式要便于计算。
在本节课的探究和学习过程中你还有那些疑惑或问题?请大胆提出来,大家共同解决。
下面我们通过感悟升华在来体会一下利用解直角三角形的知识解决实际问题的过程。
四 感悟升华
1.一架飞机以30°角俯冲400米,则飞机的高度变化情况是( )
A.升高400米
B.下降400米
C.下降200米
D.下降200米
2. 如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1m,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
3. 某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°.求旗杆的高度。(结果精确到0.1m,参考数据:sin50°≈0.77, cos50°≈0.64,tan50°≈1.19)
归纳:用锐角三角函数求某些未知量的途径往往不唯一. 正确选择关系式是关键,选择关系式常遵循以下原则:一尽量选择可以直接应用原始数据的关系式;二设法选择便于计算的关系式,若能用乘法计算应避免除法计算.
五 合作探究、学以致用
仰角、俯角对我们计算很有用,那么在实际生活中我们是怎样测量出的呢?这要用到专业的测量仪器。今天老师做了一个简易的工具。虽然测量结果有误差,但原理是相同的。
展示用半圆形量角器制作的简易测角仪,并请两位同学合作演示测量仰角和俯角的方法。
实践活动:
请同学们利用上面的工具设计一个测量学校操场旗杆顶端到地面的距离的方案。
前面的方法在计算高度时要知道到被测物体的距离,如果我们不能完整测得这个距离,还能不能求出高度呢?
六 课堂小结
通过这节课的学习你有哪些收获?
这节课我们主要研究了与仰角、俯角有关的实际问题。学习了解决实际问题时先根据题意,将实物模型转化为几何图形,正确画出示意图,如果不是直角三角形可添加适当辅助线,转化为直角三角形,利用解直角三角形的知识求解。
教学目标:
能根据直角三角形的知识解决与仰角、俯角有关的实际问题。
教学重点:
将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决。
教学难点:
学会准确分析问题并将实际问题转化成数学模型。
教学过程:
一 复习回顾
在学习新课前,我们来进行一个课前热身:
如图,在△ABC中, ∠C=90°, ∠A 、∠B 、∠C的对边分别为a,b,c 。
(1)若已知∠A的度数和 a 的长度, 则c =______, b =______.
(2)若已知∠A的度数和 b 的长度, 则c=______,a =______.
(3)若已知∠A的度数为α和 c 的长度, 则a =_____,b =____.
设计意图:充分利用学生知识最近发展区进入主题。
二 引入新课
看来大家对基础知识掌握得还是比较牢固的。下面我们来看这样一个问题:
小玲家对面新造了一幢图书大厦,小玲站在自家 窗口,望着眼前的大厦心想:“这幢图书大厦到底有多高啊?能否用所学的数学知识计算楼高呢?”
她望着大厦顶端和大厦底部,可测出视线与水平线之间的夹角各一个,这两个角如何命名呢? 即如图所示,∠α与∠β 在测量中叫什么角?
这就是我们本节所要学习的——解直角三角形的应用仰角俯角问题,并出示学习目标。
三 探究新知
1.仰角和俯角的概念
在进行测量时:
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
2.例题:小玲在自家窗口测得大厦顶部的仰角α为60°, 看这栋大厦底部的俯角β为30°,若已知两幢楼之间的距离为30m,问大厦有多高(结果取整数)?
解:在Rt△ABC中,BC=AC·tanα=30
在Rt△ADC中,CD=AC·tanβ=30×=10
∴BD=BC+CD=40≈69
∴大厦高69米
3.小结:通过解决这个实际问题,你能归纳一下利用解直角三角形的知识解决实际问题的一般过程吗?
(1)将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题)
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
设计意图:通过学生独立思考、分析阐述解题思路,培养学生逻辑推理 、语言表达等能力,培养学生运用抽象、转化、化归思想将实际问题抽象转化为数学问题。通过选择不同的关系式解决此题对比讨论得出用锐角三角函数解直角三角形关键:正确选择关系式,及选择关系式原则:一选择的关系式尽量使用原始数据,二选择关系式要便于计算。
在本节课的探究和学习过程中你还有那些疑惑或问题?请大胆提出来,大家共同解决。
下面我们通过感悟升华在来体会一下利用解直角三角形的知识解决实际问题的过程。
四 感悟升华
1.一架飞机以30°角俯冲400米,则飞机的高度变化情况是( )
A.升高400米
B.下降400米
C.下降200米
D.下降200米
2. 如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1m,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
3. 某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°.求旗杆的高度。(结果精确到0.1m,参考数据:sin50°≈0.77, cos50°≈0.64,tan50°≈1.19)
归纳:用锐角三角函数求某些未知量的途径往往不唯一. 正确选择关系式是关键,选择关系式常遵循以下原则:一尽量选择可以直接应用原始数据的关系式;二设法选择便于计算的关系式,若能用乘法计算应避免除法计算.
五 合作探究、学以致用
仰角、俯角对我们计算很有用,那么在实际生活中我们是怎样测量出的呢?这要用到专业的测量仪器。今天老师做了一个简易的工具。虽然测量结果有误差,但原理是相同的。
展示用半圆形量角器制作的简易测角仪,并请两位同学合作演示测量仰角和俯角的方法。
实践活动:
请同学们利用上面的工具设计一个测量学校操场旗杆顶端到地面的距离的方案。
前面的方法在计算高度时要知道到被测物体的距离,如果我们不能完整测得这个距离,还能不能求出高度呢?
六 课堂小结
通过这节课的学习你有哪些收获?
这节课我们主要研究了与仰角、俯角有关的实际问题。学习了解决实际问题时先根据题意,将实物模型转化为几何图形,正确画出示意图,如果不是直角三角形可添加适当辅助线,转化为直角三角形,利用解直角三角形的知识求解。
