2022-2023学年上学期湖南省安化县南金乡中学等校期中联考八年级数学(含答案)
文档属性
| 名称 | 2022-2023学年上学期湖南省安化县南金乡中学等校期中联考八年级数学(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 618.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 12:32:14 | ||
图片预览


文档简介
2022-2023学年上学期期中成果检测
初二数学
一、单选题
1.下列分式中,是最简分式的是( )
A. B. C. D.
2.代数式的值为零,则的值为( )
A. B.0 C.或0 D.1
3.若,则的值是( )
A. B. C.3 D.
4.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,设原计划平均每天生产台机器,根据题意,下面所列方程正确的是( )
A. B. C. D.
5.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( )
A.或或 B.或
C.或 D.或
6.如图,考古学家发现在地下A处有一座古墓,古墓上方是燃气管道,为了不影响管道,准备在B处和C处开工挖出“V”字形通道.若∠DBA = 120° ,∠ECA = 125°,则∠A的度数是( )
A.55° B.60° C.65° D.75°
7.如图,在中,,.若是的高,与角平分线相交于点,则的度数为( )
A. B. C. D.
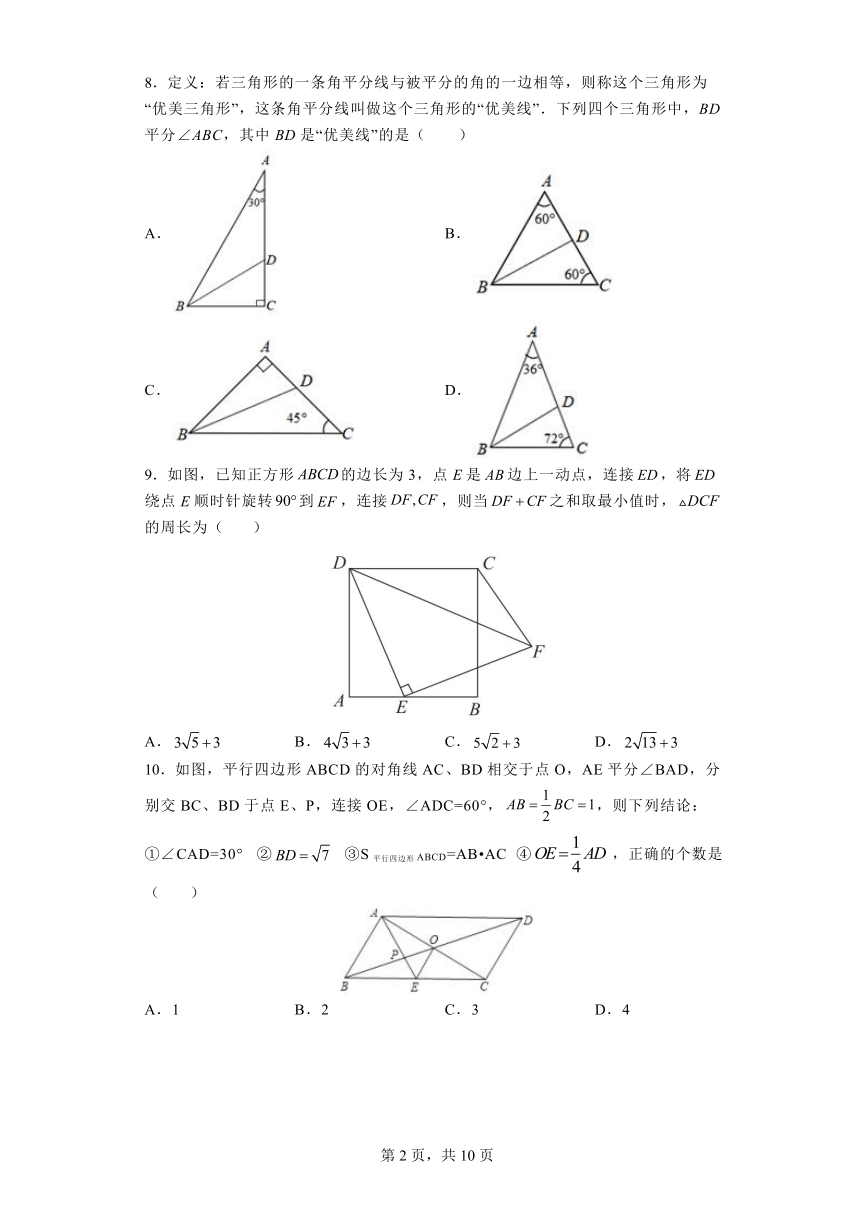
8.定义:若三角形的一条角平分线与被平分的角的一边相等,则称这个三角形为“优美三角形”,这条角平分线叫做这个三角形的“优美线”.下列四个三角形中,BD平分∠ABC,其中BD是“优美线”的是( )
A. B.
C. D.
9.如图,已知正方形的边长为3,点E是边上一动点,连接,将绕点E顺时针旋转到,连接,则当之和取最小值时,的周长为( )
A. B. C. D.
10.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,,则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB AC ④ ,正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.计算: .
12.如果关于的方程有增根,那么 .
13.如图,已知AB=AD,∠BAE=∠DAC,要使,若以“SAS”为依据,补充的条件是 .
14.如图,线段,用尺规作图法按如下步骤作图.
(1)过点B作的垂线,并在垂线上取;
(2)连接,以点C为圆心,为半径画弧,交于点E;
(3)以点A为圆心,为半径画弧,交于点D.即点D为线段的黄金分割点.
则线段的长度约为 (结果保留两位小数,参考数据:)
三、解答题
15.计算:
(1)
(2)先化简:,再从1,2,3,4中选择一个合适的数作为的值代入求值.
16.中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化.年月日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用元购进了种茶叶若干盒,用元购进B种茶叶若干盒,所购B种茶叶比种茶叶多盒,且B种茶叶每盒进价是种茶叶每盒进价的倍.求,B两种茶叶每盒进价分别为多少元?
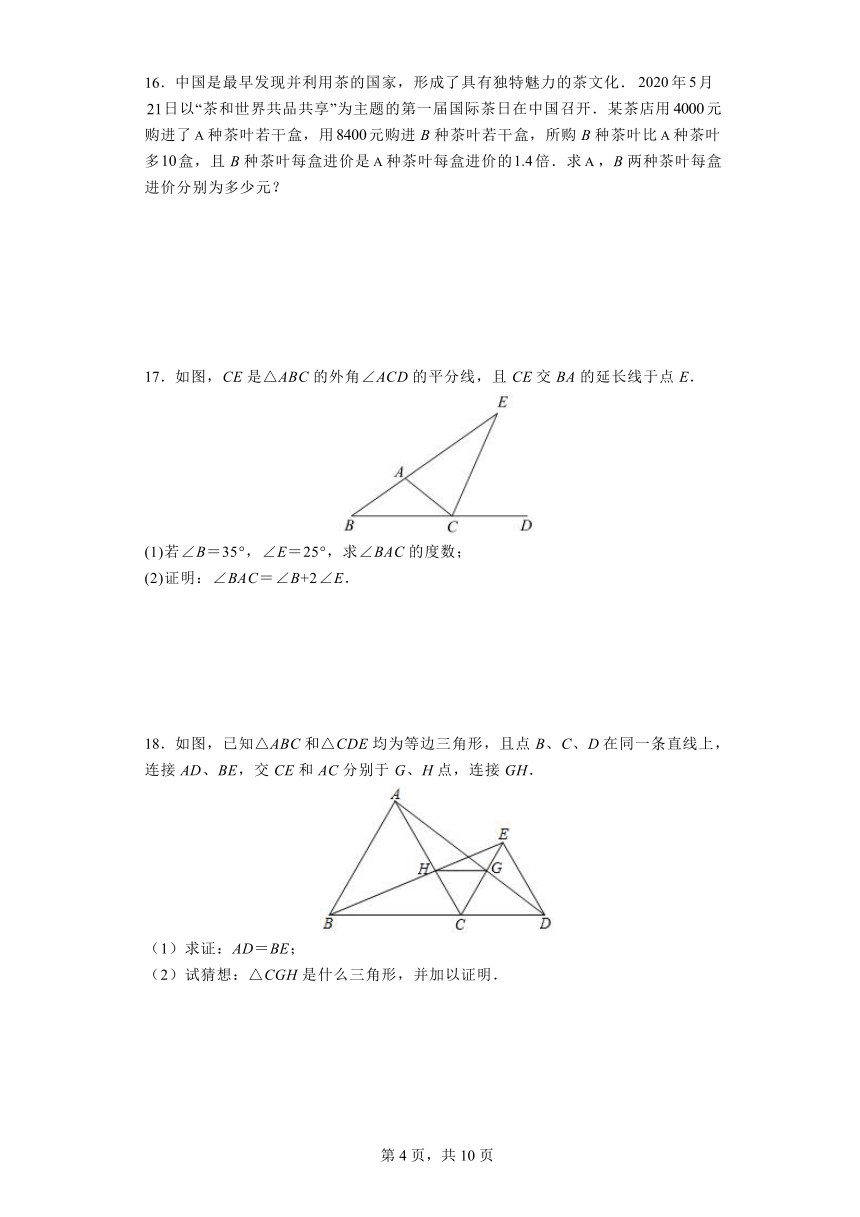
17.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=35°,∠E=25°,求∠BAC的度数;
(2)证明:∠BAC=∠B+2∠E.
18.如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
(1)求证:AD=BE;
(2)试猜想:△CGH是什么三角形,并加以证明.
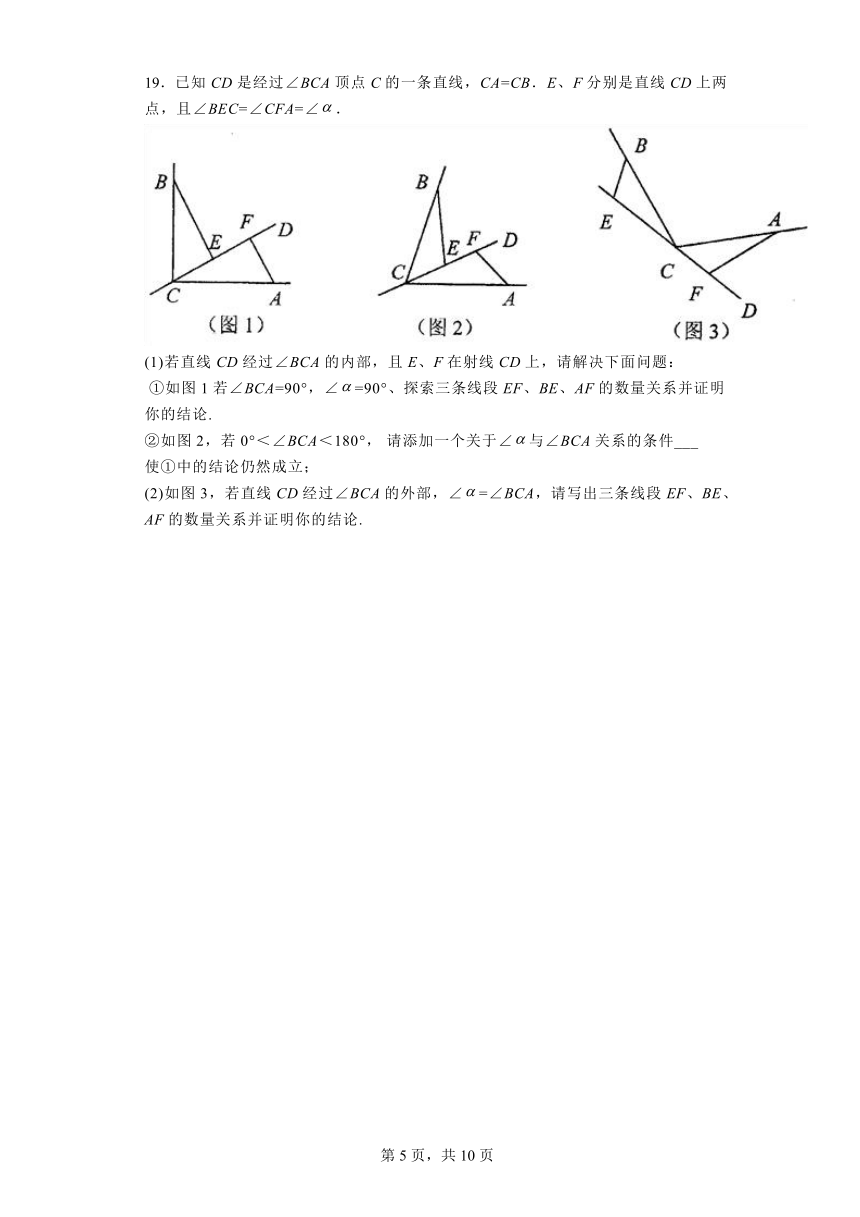
19.已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠与∠BCA关系的条件___ 使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
参考答案
1-10 DBAAA CADAD
11.2 12.1 13.AC=AE. 14.6.18
15.(1);(2),当时,原式;当时,原式
16.
17.
18.
19.(1)①如图1中,.
.
E点在F点的左侧,.
∵BE⊥CD,AF⊥CD,∠ACB=90°,.
∴∠BEC=∠AFC=90°,.
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
证明:如图2中,.
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..
理由是:如图3中,.
.
∵∠BEC=∠CFA=∠a,∠a=∠BCA,.
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,.
∴∠EBC+∠BCE=∠BCE+∠ACF,.
∴∠EBC=∠ACF,.
在△BEC和△CFA中,.
,.
∴△BEC≌△CFA(AAS),.
∴AF=CE,BE=CF,.
∵EF=CE+CF,.
∴EF=BE+AF.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
初二数学
一、单选题
1.下列分式中,是最简分式的是( )
A. B. C. D.
2.代数式的值为零,则的值为( )
A. B.0 C.或0 D.1
3.若,则的值是( )
A. B. C.3 D.
4.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,设原计划平均每天生产台机器,根据题意,下面所列方程正确的是( )
A. B. C. D.
5.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( )
A.或或 B.或
C.或 D.或
6.如图,考古学家发现在地下A处有一座古墓,古墓上方是燃气管道,为了不影响管道,准备在B处和C处开工挖出“V”字形通道.若∠DBA = 120° ,∠ECA = 125°,则∠A的度数是( )
A.55° B.60° C.65° D.75°
7.如图,在中,,.若是的高,与角平分线相交于点,则的度数为( )
A. B. C. D.
8.定义:若三角形的一条角平分线与被平分的角的一边相等,则称这个三角形为“优美三角形”,这条角平分线叫做这个三角形的“优美线”.下列四个三角形中,BD平分∠ABC,其中BD是“优美线”的是( )
A. B.
C. D.
9.如图,已知正方形的边长为3,点E是边上一动点,连接,将绕点E顺时针旋转到,连接,则当之和取最小值时,的周长为( )
A. B. C. D.
10.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,,则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB AC ④ ,正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.计算: .
12.如果关于的方程有增根,那么 .
13.如图,已知AB=AD,∠BAE=∠DAC,要使,若以“SAS”为依据,补充的条件是 .
14.如图,线段,用尺规作图法按如下步骤作图.
(1)过点B作的垂线,并在垂线上取;
(2)连接,以点C为圆心,为半径画弧,交于点E;
(3)以点A为圆心,为半径画弧,交于点D.即点D为线段的黄金分割点.
则线段的长度约为 (结果保留两位小数,参考数据:)
三、解答题
15.计算:
(1)
(2)先化简:,再从1,2,3,4中选择一个合适的数作为的值代入求值.
16.中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化.年月日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用元购进了种茶叶若干盒,用元购进B种茶叶若干盒,所购B种茶叶比种茶叶多盒,且B种茶叶每盒进价是种茶叶每盒进价的倍.求,B两种茶叶每盒进价分别为多少元?
17.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=35°,∠E=25°,求∠BAC的度数;
(2)证明:∠BAC=∠B+2∠E.
18.如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
(1)求证:AD=BE;
(2)试猜想:△CGH是什么三角形,并加以证明.
19.已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠与∠BCA关系的条件___ 使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
参考答案
1-10 DBAAA CADAD
11.2 12.1 13.AC=AE. 14.6.18
15.(1);(2),当时,原式;当时,原式
16.
17.
18.
19.(1)①如图1中,.
.
E点在F点的左侧,.
∵BE⊥CD,AF⊥CD,∠ACB=90°,.
∴∠BEC=∠AFC=90°,.
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
证明:如图2中,.
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..
理由是:如图3中,.
.
∵∠BEC=∠CFA=∠a,∠a=∠BCA,.
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,.
∴∠EBC+∠BCE=∠BCE+∠ACF,.
∴∠EBC=∠ACF,.
在△BEC和△CFA中,.
,.
∴△BEC≌△CFA(AAS),.
∴AF=CE,BE=CF,.
∵EF=CE+CF,.
∴EF=BE+AF.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
同课章节目录
