人教版八年级下册 18.2.3 正方形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册 18.2.3 正方形 同步练习(含答案) | 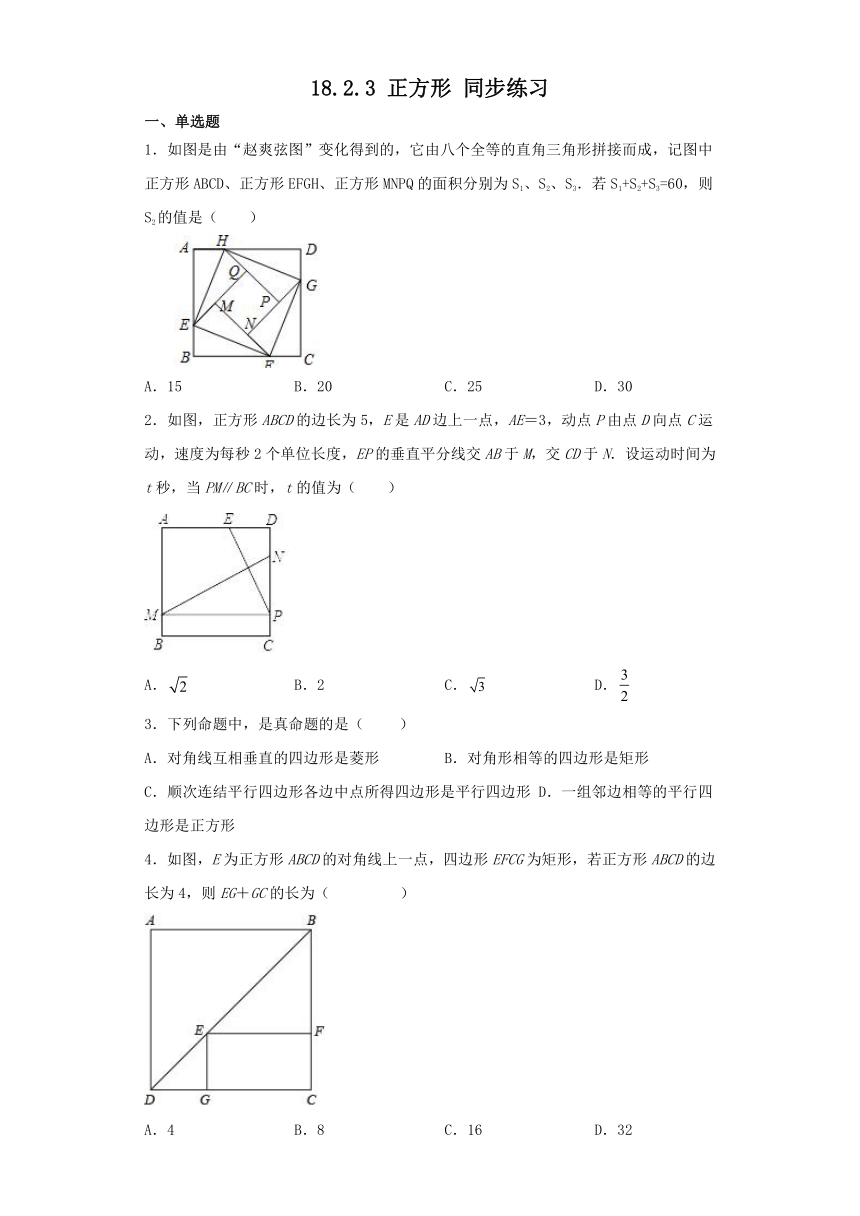 | |
| 格式 | docx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 12:38:56 | ||
图片预览



文档简介
18.2.3 正方形 同步练习
一、单选题
1.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是( )
A.15 B.20 C.25 D.30
2.如图,正方形ABCD的边长为5,E是AD边上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线交AB于M,交CD于N.设运动时间为t秒,当PM∥BC时,t的值为( )
A. B.2 C. D.
3.下列命题中,是真命题的是( )
A.对角线互相垂直的四边形是菱形 B.对角形相等的四边形是矩形
C.顺次连结平行四边形各边中点所得四边形是平行四边形 D.一组邻边相等的平行四边形是正方形
4.如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A.4 B.8 C.16 D.32
5.下列命题中,正确的是( )
A.平行四边形的对角线相等 B.矩形的对角线互相垂直
C.对角线互相垂直且平分的四边形是菱形 D.对角线相等且垂直的四边形是正方形
6.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
A.1 B.2018 C.2019 D.2020
7.下列命题中,假命题是( )
A.两组对边平行的四边形是平行四边形 B.三个角是直角的四边形是矩形
C.四条边相等的四边形是菱形 D.有一个角是直角的平行四边形是正方形
8.下列命题中的真命题是( )
A.有一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相垂直平分的四边形是正方形
D.有一组邻边相等的平行四边形是菱形
9.如图①,点从菱形的顶点出发,沿以的速度匀速运动到点.图②是点运动时,的面积()随着时间()变化的关系图象,则菱形的边长为( )
A. B. C. D.
10.如图,已知,是正方形的对角线上的两点,,,则四边形的周长是( )
A. B. C. D.
二、填空题
11.正方形的性质∶
①边∶_______都相等且_______;
②角:四个角都是_______;
③对角线:两条对角线互相_______且_______,并且每一条对角线平分_______;
④正方形既是_______图形,又是_______图形,正方形有_______对称轴.
12.如图,请给矩形ABCD添加一个条件,使它成为正方形,则此条件可以为________.
13.如图,点P为线段AB上的一个动点,AB=6,以PA、PB为边向同侧作正方形APDC、正方形PBEF,两正方形的对角线的交点分别记为O1、O2,连接O1O2,则O1O2的最小值为_____.
14.如图,正方形的边长为1,以对角线为边作第二个正方形,再以对角线为边作第三个正方形,…,则第二个正方形的面积为_____________,第n个正方形的面积为_____________(用含n的代数式表示).
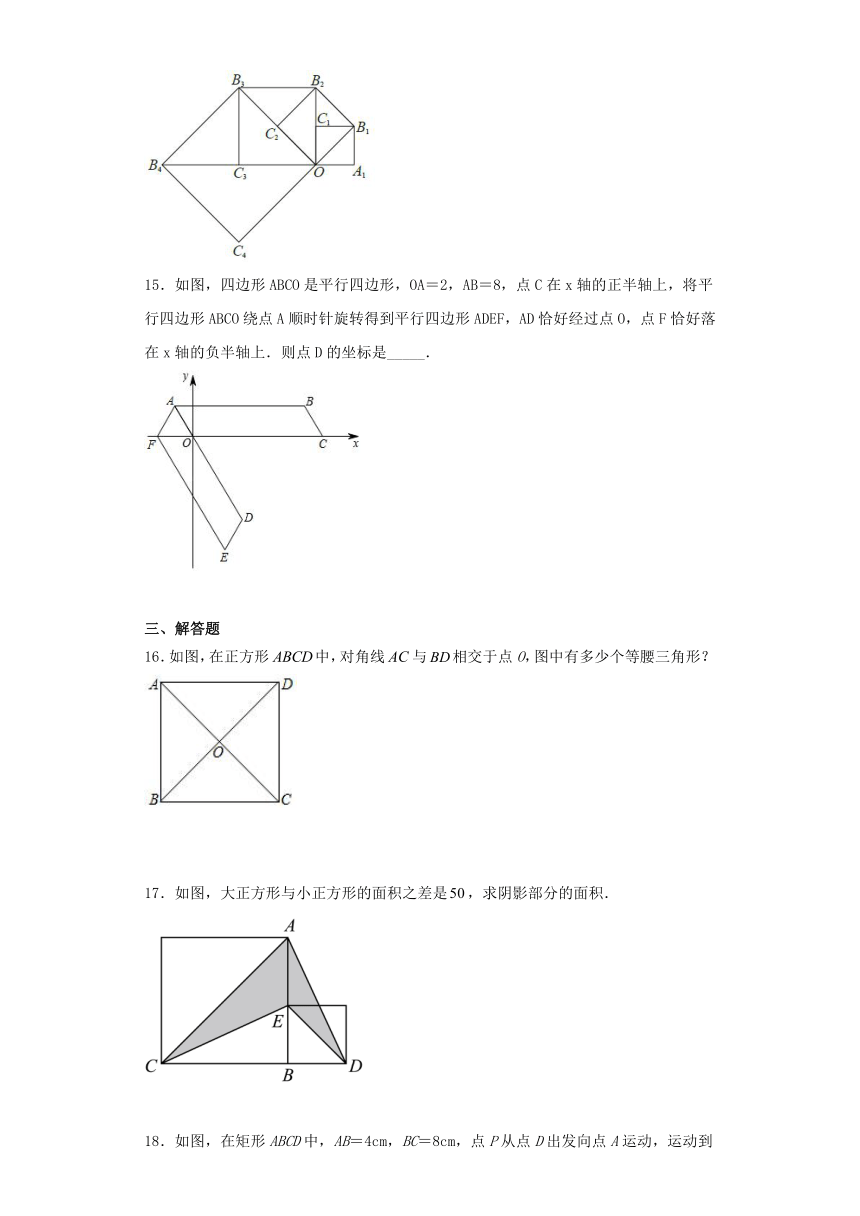
15.如图,四边形ABCO是平行四边形,OA=2,AB=8,点C在x轴的正半轴上,将平行四边形ABCO绕点A顺时针旋转得到平行四边形ADEF,AD恰好经过点O,点F恰好落在x轴的负半轴上.则点D的坐标是_____.
三、解答题
16.如图,在正方形中,对角线与相交于点O,图中有多少个等腰三角形?
17.如图,大正方形与小正方形的面积之差是,求阴影部分的面积.
18.如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度都是1cm/s,连接PQ,AQ,CP,设点P、Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
19.如图,点,,分别在正方形的边,,上,,且.求证:.
20.如图,在中,,,,点D从点C出发沿方向以2/秒的速度向点A匀速运动,同时点E从点A出发沿方向以1/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(),过点D作于点F,连接,.
(1)求证:;
(2)四边形能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形能否为正方形?若能,求出t的值;若不能,请说明理由.
参考答案
1.B
2.B
3.C
4.A
5.C
6.D
7.D
8.D
9.C
10.A
11. 四条边 对边平行 直角 垂直平分 相等 一组对角 中心对称 轴对称 四条
12.
13.3
14. 2
15.(3,﹣3)
16.图中有8个等腰三角形,并且都是等腰直角三角形.
17.阴影部分的面积为25
18.(1)4s
(2)3s
(3)菱形AQCP的周长是20cm,面积是20cm2
19. 【详解】证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵,
∴∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
在△BEF和△CFG中,
∵∠B=∠C=90°,∠BEF=∠CFG,,
∴△BEF≌△CFG,
∴BE=CF.
20.
(1)证明:∵中,,,∴.又∵在中,,∴,∴;
(2)解:能构成菱形,理由如下:∵,,∴四边形是平行四边形,当时,四边形是菱形,即,解得:,即当时,四边形是菱形;
(3)解:四边形不能为正方形,理由如下:当时,.∴∴∵,∴,∴,∴,∴时,∵,∴,∴,∴四边形不可能为正方形.
一、单选题
1.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是( )
A.15 B.20 C.25 D.30
2.如图,正方形ABCD的边长为5,E是AD边上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线交AB于M,交CD于N.设运动时间为t秒,当PM∥BC时,t的值为( )
A. B.2 C. D.
3.下列命题中,是真命题的是( )
A.对角线互相垂直的四边形是菱形 B.对角形相等的四边形是矩形
C.顺次连结平行四边形各边中点所得四边形是平行四边形 D.一组邻边相等的平行四边形是正方形
4.如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A.4 B.8 C.16 D.32
5.下列命题中,正确的是( )
A.平行四边形的对角线相等 B.矩形的对角线互相垂直
C.对角线互相垂直且平分的四边形是菱形 D.对角线相等且垂直的四边形是正方形
6.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
A.1 B.2018 C.2019 D.2020
7.下列命题中,假命题是( )
A.两组对边平行的四边形是平行四边形 B.三个角是直角的四边形是矩形
C.四条边相等的四边形是菱形 D.有一个角是直角的平行四边形是正方形
8.下列命题中的真命题是( )
A.有一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相垂直平分的四边形是正方形
D.有一组邻边相等的平行四边形是菱形
9.如图①,点从菱形的顶点出发,沿以的速度匀速运动到点.图②是点运动时,的面积()随着时间()变化的关系图象,则菱形的边长为( )
A. B. C. D.
10.如图,已知,是正方形的对角线上的两点,,,则四边形的周长是( )
A. B. C. D.
二、填空题
11.正方形的性质∶
①边∶_______都相等且_______;
②角:四个角都是_______;
③对角线:两条对角线互相_______且_______,并且每一条对角线平分_______;
④正方形既是_______图形,又是_______图形,正方形有_______对称轴.
12.如图,请给矩形ABCD添加一个条件,使它成为正方形,则此条件可以为________.
13.如图,点P为线段AB上的一个动点,AB=6,以PA、PB为边向同侧作正方形APDC、正方形PBEF,两正方形的对角线的交点分别记为O1、O2,连接O1O2,则O1O2的最小值为_____.
14.如图,正方形的边长为1,以对角线为边作第二个正方形,再以对角线为边作第三个正方形,…,则第二个正方形的面积为_____________,第n个正方形的面积为_____________(用含n的代数式表示).
15.如图,四边形ABCO是平行四边形,OA=2,AB=8,点C在x轴的正半轴上,将平行四边形ABCO绕点A顺时针旋转得到平行四边形ADEF,AD恰好经过点O,点F恰好落在x轴的负半轴上.则点D的坐标是_____.
三、解答题
16.如图,在正方形中,对角线与相交于点O,图中有多少个等腰三角形?
17.如图,大正方形与小正方形的面积之差是,求阴影部分的面积.
18.如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度都是1cm/s,连接PQ,AQ,CP,设点P、Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
19.如图,点,,分别在正方形的边,,上,,且.求证:.
20.如图,在中,,,,点D从点C出发沿方向以2/秒的速度向点A匀速运动,同时点E从点A出发沿方向以1/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(),过点D作于点F,连接,.
(1)求证:;
(2)四边形能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形能否为正方形?若能,求出t的值;若不能,请说明理由.
参考答案
1.B
2.B
3.C
4.A
5.C
6.D
7.D
8.D
9.C
10.A
11. 四条边 对边平行 直角 垂直平分 相等 一组对角 中心对称 轴对称 四条
12.
13.3
14. 2
15.(3,﹣3)
16.图中有8个等腰三角形,并且都是等腰直角三角形.
17.阴影部分的面积为25
18.(1)4s
(2)3s
(3)菱形AQCP的周长是20cm,面积是20cm2
19. 【详解】证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵,
∴∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
在△BEF和△CFG中,
∵∠B=∠C=90°,∠BEF=∠CFG,,
∴△BEF≌△CFG,
∴BE=CF.
20.
(1)证明:∵中,,,∴.又∵在中,,∴,∴;
(2)解:能构成菱形,理由如下:∵,,∴四边形是平行四边形,当时,四边形是菱形,即,解得:,即当时,四边形是菱形;
(3)解:四边形不能为正方形,理由如下:当时,.∴∴∵,∴,∴,∴,∴时,∵,∴,∴,∴四边形不可能为正方形.
