【备考2023】湖南省娄底市中考数学模拟试卷3(含解析)
文档属性
| 名称 | 【备考2023】湖南省娄底市中考数学模拟试卷3(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-07 15:35:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【备考2023】湖南省娄底市中考数学模拟试卷3
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一个选项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.下列说法正确的是( )
A.倒数等于他本身的数只有1 B.平方等于他本身的数只有1和0
C.立方等于他本身的数只有1 D.绝对值等于他本身的数只有正数
2.在下列各式的计算中,正确的是( )
A. B.
C. D.
3.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩(分) 80 85 90 95
人数(人) 1 2 5 2
则这组数据的中位数和众数分别为( )
A.90,89 B.90,90 C.90,90.5 D.9
4.下面图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
5.据中国互联网络信息中心(CNNIC)在京发布的《中国互联网络发展状况统计报告》,截至2019年6月底,我国4G手机用户数达到5.74亿户,将5.74亿这个数用科学记数法可表示为( )
A. B. C. D.
6.如图,直线a,b相交于点O,若,则等于( )
A. B. C. D.
7.将不等式组的解集表示在数轴上,下列表示正确的是( )
A. B.
C. D.
8.某个一次函数的图象与直线平行,并且经过点,则这个一次函数的解析式为( )
A. B. C. D.
9.一次函数y=kx+b的图象与y轴的交点的纵坐标为-5,且当x=1时,y=-2,那么这个函数的表达式是( )
A.y=4x-6 B.y=-3x-5 C.y=3x+5 D.y=3x-5
10.观察下列等式:,,,,,,…,根据其中的规律可得的结果的个位数字是( )
A. B. C. D.
11.如图,△AOB和△ACD均为正三角形,且顶点B、D均在双曲线(x>0)上,连接BC交AD于P,连接OP,则图中是( )
A. B.3 C.6 D.12
12.定义:如果(,且),那么x叫做以a为底N的对数,记做.例如:因为,所以;因为,所以.下列说法:①;②;③若,则;④;正确的序号有( )
A.①③ B.②③ C.①②③ D.②③④
二、填空题(本大题共6小题,每小题3分,满分18分)
13.若有意义,则的取值范围是_________.
14.若关于的一元二次方程的一个根是,则另一个根是_____________________.
15.口袋里有大小相同的8个红球、4个白球和4个黄球,从中任意摸出1个球,摸出红球的可能性是____.
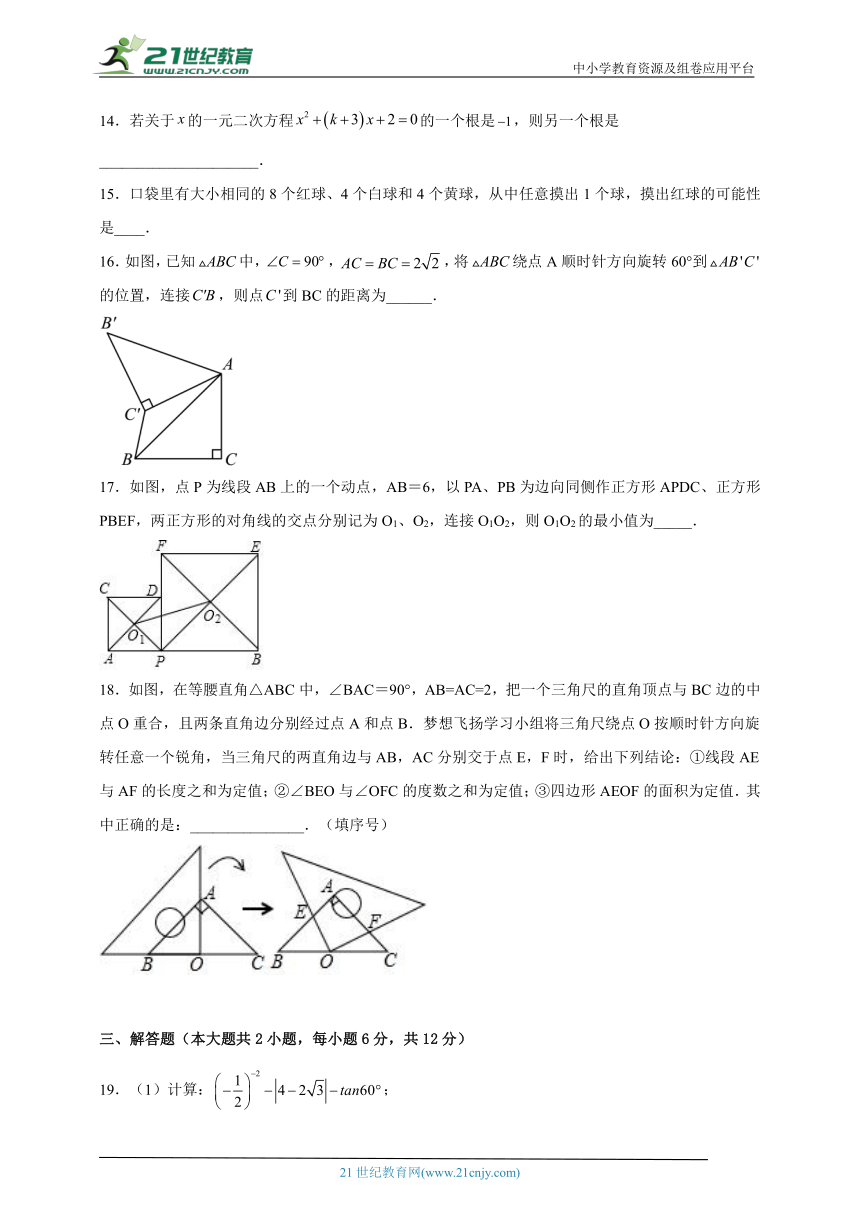
16.如图,已知中,,,将绕点A顺时针方向旋转60°到的位置,连接,则点到BC的距离为______.
17.如图,点P为线段AB上的一个动点,AB=6,以PA、PB为边向同侧作正方形APDC、正方形PBEF,两正方形的对角线的交点分别记为O1、O2,连接O1O2,则O1O2的最小值为_____.
18.如图,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,把一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B.梦想飞扬学习小组将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,给出下列结论:①线段AE与AF的长度之和为定值;②∠BEO与∠OFC的度数之和为定值;③四边形AEOF的面积为定值.其中正确的是:_______________.(填序号)
三、解答题(本大题共2小题,每小题6分,共12分)
19.(1)计算:;
(2)化简:.
20.先化简,再求值:,其中x是不等式的最大整数解.
四、解答题(本大题共2小题,每小题8分,共16分)
21.奉节脐橙丰收了,某镇为帮助果农扩大销量,利用网络平台直播带货进行销售.为了解平台在一个季度内每天的销售额,从中随机抽取了20天的销售额(单位:万元)作为样本,数据如下:
15,14,15,15,14,16,12,13,13,16,16,14,13,17,15,14,16,17,14,14
(1)根据上述样本数据,补全条形统计图;
(2)上述样本数据的众数是____________万元,中位数是_____________万元;
(3)该网络平台一共有两男两女四名主播,每天随机有两名主播进行直播带货,请用树状图或者列表的方法求出某一天刚好主播是一男一女的概率是多少?
22.由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用.
(1)求出线段OA和双曲线函数表达式;
(2)从消毒开始,至少在多少分钟内,师生不能待在教室?
五、解答题(本大题共2小题,每小题9分,共18分)
23.森泽家买了一套住房有三个卧室,其中A卧室的地面面积为,B卧室的地面面积为,设C卧室地面面积的数值为m,且;
(1)求m的值(用含有x、y的式子表示);
(2)森泽想把所有卧室的地面都铺上地砖,恰好每平方米地砖费用也是40元,且满足:m比x大10,y是最小的正整数,求铺地砖的总费用是多少元?
(3)在(2)的条件下,森泽想把墙面也铺上壁纸,已知墙面的总面积比地面总面积5倍多15平方单位,某厂家有两个车间可以生产这批壁纸,其中,第二车间比第一车间人数的少3人,如果从第二车间调出10人到第一车间,那么第二车间的人数是第一车间人数的一半,两个车间的每位工人每天可以生产0.5平方单位壁纸,若第一车间和第二车间共同为森泽家生产这批壁纸,几天可以完工?
24.如图,△ABC内接于, AB为直径,∠ACB 的平分线分别交AB于点D.交于点E,过点E作的切线,交CE的平行线AF于点F.
(1)求证:四边形ADEF为平行四边形.
(2)若tan∠CAB=,AF=5,求四边形ADEF的面积.
六、综合题(本大题共2小题,每小题10分,共20分)
25.综合与实践,如图,在Rt△ABC中,,,AD、CE分别是∠BAC、∠BCA的平分线,AD与CE相交于点F,交BC于点M,交AB于点N,连接BF.
(1)∠EFA的度数为 .
(2)求证:.
(3)若,求CD的长.
26.如图,直线交x轴于点A,交y轴于点B,点C在y轴上,,经过点A,C的抛物线交直线AB于另一点D.
(1)求抛物线的解析式;
(2)点P为直线AB上方抛物线上一点,过点P作轴于点F,交AB于点E.当时,求点P的坐标;
(3)抛物线与x轴的另一个交点为K,过点的任意直线MN(不与y轴平行)与抛物线交于点M,N,直线KM,KN分别交y轴于点G,H,是否存在t的值使得OG与OH的积为定值?若存在,求t的值,若不存在,请说明理由.
参考答案:
1.【分析】根据倒数、平方、立方、绝对值的概念对各选项逐一判断即可得出答案.
解:A.倒数等于他本身的数有、,故此选项不符合题意;
B.平方等于他本身的数有、,故此选项符合题意;
C.立方等于他本身的数有、、,故此选项不符合题意;
D.绝对值等于他本身的数有和正数,故此选项不符合题意.
故选:B.
【点评】本题考查倒数、平方、立方、绝对值的概念.理解和掌握相关的概念是解题的关键.
2.【分析】利用合并同类项的法则以及积的乘方、幂的乘方,平方差公式即可判断.
解:A. 不是同类项,不能合并,故选项错误;
B. ,选项正确;
C. ,故选项错误;
D. ,故选项错误.
故选:B.
【点评】本题考查幂的乘方与积的乘方,平方差公式,单项式乘多项式,合并同类项,解题关键在于掌握运算法则.
3.【分析】先把这些数从小到大排列,根据众数及中位数的定义求出众数和中位数.
解:在这一组数据中90是出现次数最多的,故众数是90,
而将这组数据从小到大的顺序排列后,处于中间位置的那个数是90、90,
那么由中位数的定义可知,这组数据的中位数是90.
故选:B.
【点评】本题主要考查众数与中位数,众数是一组数据中出现次数最多的数,中位数是将一组数据从小到大(或从大到小)重新排列后,若有奇数个数据,最中间的那个数,若有偶数个数据,最中间两个数的平均数,叫做这组数据的中位数,掌握众数和中位数的定义是解题的关键.
4.【分析】根据轴对称图形的定义和中心对称图形的定义对每个选项进行判断即可.
解:A项是轴对称图形,不是中心对称图形;
B项是中心对称图形,不是轴对称图形;
C项是中心对称图形,不是轴对称图形;
D项是中心对称图形,也是轴对称图形;
故选:D.
【点评】本题考查了轴对称图形的定义和中心对称图形的定义,掌握知识点是解题关键.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
5.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
解:5.74亿用科学记数法表示为:.
故答案为:.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
6.【分析】根据对顶角相等可得,再由邻补角的定义即可求解.
解:∵,
∴,
∴,
故选:C.
【点评】本题主要考查了对顶角相等,解题的关键是正确掌握对顶角的性质和邻补角的定义.
7.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:由x+4>4,得:x>0,
由1-2x>-1,得:x<1,
则不等式组的解集为0<x<1,
在数轴上表示为
故选:B.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
8.【分析】根据两直线平行时k的值相等,设出所求解析式,把已知点坐标代入计算即可.
解:由一次函数的图象与直线y═x+6平行,设直线解析式为y=x+b,
把( 2, 4)代入得: 4= 1+b,即b= 3,
则这个一次函数解析式为y=x 3.
故选:C.
【点评】此题考查了待定系数法求一次函数解析式,以及一次函数的图象,熟练掌握待定系数法是解本题的关键.
9.【分析】根据题意,先把(1,-2)、(0,-5)代入y=kx+b中,得到关于k、b的二元一次方程组,然后解方程组即可.
解:把(1,-2)、(0,-5)代入y=kx+b中,
得,
解得.
故一次函数的解析式是y=3x-5.
故选D.
【点评】本题考查了待定系数法求一次函数解析式,解题的关键是掌握y轴上点的横坐标为0及二元一次方程组的解法.
10.【分析】由已知可得尾数,,,的规律是4个数一循环,则的结果的个位数字与的个位数字相同,即可求解.
解:∵,,,,,,…,
∴尾数,,,的规律是4个数一循环,
∵,
∴的个位数字是,
又∵,
∴的结果的个位数字与的个位数字相同,
∴的结果的个位数字是.
故选:A.
【点评】本题考查数的尾数特征,能够通过所给数的特点,确定尾数的循环规律是解题的关键.
11.【分析】先根据△AOB和△ACD均为正三角形可知,故可得出ADOB,所以,故,过点B作BE⊥OA于点E,由反比例函数系数k的几何意义即可得出结论.
解:如图:
∵△AOB和△ACD均为正三角形,
∴,
∴ADOB,
∴,
∴,
过点B作BE⊥OA于点E,则,
∵点B在反比例函数的图象上,
∴,
∴.
故选:C.
【点评】本题考查的是反比例函数,等边三角形的性质及反比例函数系数k的几何意义等知识,综合运用以上知识是解题的关键.
12.【分析】由新定义可得:利用新定义逐一计算判断,从而可得答案.
解:根据新定义可得: 故①不符合题意;
故②符合题意;
,
解得: 故③符合题意;
,故④符合题意,
故选D
【点评】本题考查的新定义运算,有理数的乘方运算的含义,正确理解新定义,运用新定义解决问题是解本题的关键.
13.【分析】根据二次根式有意义的条件,被开方数大于等于0,以及分母不等于0,即可求的取值范围.
解:根据题意得:,,
解得且.
故答案为:且.
【点评】主要考查了二次根式以及分式有意义的条件.解题的关键是二次根式中的被开方数必须是非负数,否则二次根式无意义;分式有意义的条件是分母不等于零.
14.【分析】根据根与系数的关系计算即可.
解:设另一个根为,则,解得
故答案为
【点评】本题考查一元二次方程根与系数的关系,熟记公式是解题的关键,也可以把代入方程求出k的值再解方程.
15.【分析】根据红球的个数÷总个数=摸出红球的可能性即可得出答案.
解:8+4+4=16(个),
,
故摸到红球的可能性是.
故答案为.
【点评】本题考查简单概率计算.对于这类题目,看红球被摸到的可能性是几分之几,就看红球占总数的几分之几就可以了.
16.【分析】过点作E⊥AC于E,D⊥BC于D,得到四边形DCE是矩形,由∠AC=60°,得到∠AE=30°,求出AE,由此求出答案.
解:过点作E⊥AC于E,D⊥BC于D,
∵,
∴四边形DCE是矩形,
∵A=AC=,∠AC=60°,
∴∠AE=30°,
∴,
∴D=CE=-=,
故答案为:.
【点评】此题考查旋转的性质,矩形的判定定理及性质定理,直角三角形30度角的性质,熟记矩形的判定及旋转的性质是解题的关键.
17.【分析】作O1M⊥AP于M,O2N⊥PB于N,O1Q⊥O2N于Q,如图,利用正方形的性质得△AO1P和△PO2B都是等腰直角三角形,则AM=PM,PN=BN,所以MN=AB=3,再证明四边形O1MNO2为矩形得到O1Q=MN=3,然后根据垂线段最短得到O1O2的最小值.
解:作O1M⊥AP于M,O2N⊥PB于N,O1Q⊥O2N于Q,如图,
∵四边形APDC和四边形PBEF都为正方形,
,
∴△AO1P和△PO2B都是等腰直角三角形,
∵O1M⊥AP,O2N⊥PB,
∴AM=PM,PN=BN,
∴MN=PM+PN=AB=3,
∵O1M⊥AP,O2N⊥PB,O1Q⊥O2N,
,
∴四边形O1MNO2为矩形,
∴O1Q=MN=3,
∵O1O2≥O1Q,
∴O1O2的最小值为3.
故答案为:3.
【点评】本题主要考查正方形的性质,等腰三角形的性质,垂线段最短,掌握正方形的性质,等腰三角形的性质,垂线段最短是解题的关键.
18.【分析】连接,先证,利用全等三角形的性质可得出,进而可得出,结论①正确;由三角形的内角和定理、结合,可得,结论②正确;由可得出,结合图形可得出,结论③正确.
解:如图,连接,
为等腰直角三角形,点为的中点,
,,.
,,
.
在和中,,
,
,
,则结论①正确;
,,,
,则结论②正确;
,
,
,则结论③正确;
综上,正确的结论是①②③,
故答案为:①②③.
【点评】本题考查了三角形全等的判定定理与性质、等腰直角三角形等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.
19.【分析】(1)先算乘方、绝对值和特殊三角函数值,再算加减法即可.
(2)根据完全平方公式和平方差公式化简式子,再合并同类项即可.
解:(1)
.
(2)
.
【点评】本题考查了实数的混合运算和化简多项式的问题,掌握实数混合运算法则、绝对值的性质、特殊三角函数值、完全平方公式、平方差公式是解题的关键.
20.【分析】先化简分式,再求出不等式的解集,确定x的值即可.
解:
解不等式,得不等式的解集:
∴最大整数解:
当时,
原式.
【点评】本题主要考查了分式的化简求值与一元一次不等式的整数解,解题的关键是能够正确的化简分式和求出一元一次不等式的整数解.
21.【分析】(1)根据题目中的数据,可以得到销售额14万元和16万元的天数,然后即可将条形统计图补充完整;
(2)根据条形统计图中的数据,可以直接写出样本数据的众数,计算出样本数据的中位数;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到一男和一女的情况,再利用概率公式即可求得答案.
解:(1)由题目中的数据可得,
销售额为14万元的有6天,销售额为16万元的有4天,
补全的条形统计图如右图所示;
(2)由条形统计图可得,
样本数据的众数是14万元,中位数是(万元),
故答案为:14,14.5;
(3)画树状图得:
∵共有12种等可能的结果,抽取的两人恰好是一男和一女的有8种结果,
∴抽取的两人恰好是一男和一女的概率为.
【点评】本题考查条形统计图、中位数、众数、树状图法与列表法求概率,解答本题的关键是明确条形统计图的特点,会计算一组数据的中位数和加权平均数.用到的知识点为:概率=所求情况数与总情况数之比.
22.【分析】(1)先求解反比例函数解析式,再求解当时,的值,再求解段的解析式,从而可得答案;
(2)分别求解当时,的值,再结合函数图象可得答案.
解:(1)设反比例函数为:
把代入得:
当时,
设段为:
把代入得: 则
段为:
(2)如图,直线与函数图象交于两点,
把代入得:
把代入得:
所以从消毒开始,至少在分钟内,师生不能待在教室.
【点评】本题考查的是正比例函数与反比例函数的实际应用,利用待定系数法求解正比例与反比例函数的解析式,以及正比例与反比例图象上的点的坐标特点,掌握以上知识是解题的关键.
23.【分析】(1)由代入A、B进行整式的加减运算,注意括号、负号的作用;
(2)由y为最小正整数,得到,由m比x大10,得到,继而解得,,再解得铺地砖的总费用,代入数值解题即可;
(3)设第一车间人数为x人,则第二车间人数人,根据题意列方程,解方程即可求出x,进一步即可求出结果.
解:(1)
答:m值为.
(2)∵y为最小正整数,∴,
∵m比x大10,∴
当,时,
(元)
答:总费用为5760元
(3)设第一车间人数为x人,则第二车间人数人.
(人)
(平方单位)
(平方单位)
天
答:14天可以完工.
【点评】本题考查整式的加减、整式的化简求值、一元一次方程的实际应用等知识,是重要考点,掌握相关知识是解题关键.
24.【分析】(1)连接OE,由AB为直径可得,由CE平分可得,利用同弧所对的圆心角是圆周角的2倍,可得,由EF为的切线,可得,根据同旁内角互补,两直线平行,可得,又因为,即可得出结论;
(2)过点A作交CE于点G,利用相似三角形的判定与性质,以及勾股定理,即可求解.
(1)证明:连接OE,如图,
∵AB为直径,
∴,
∵CE平分,
∴,
∴,
∵EF为的切线,
∴,
∵,
∴,
∵,即,
∴四边形ADEF为平行四边形;
(2)解:过点A作交CE于点G,如图,
∵tan∠CAB=,
∴,
设,
,
,
∵,,
,
,
,
在和中,
,
,
,
,
,
∵四边形ADEF为平行四边形,AF=5,
,
,
,
,
,
,
解得,
(舍去),
.
【点评】本题主要考查了圆周角定理、角平分线的定义、平行四边形的判定、勾股定理与相似三角形的判定与性质.
25.【分析】(1)根据角平分线的定义得∠DAC=∠BAD∠BAC=15°,∠ACE=∠BCE∠ACB=45°,根据三角形外角的性质即可求解;
(2)根据条件可得到FM=FN,再根据角的度数可求得∠FDC=75°=∠FEN,可证明△EFN≌△DFM,可得到EF=DF.
(3)作FH⊥AC于H,根据角平分线的性质可得,根据,可得,即可求解.
解:(1)在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠DAC=∠BAD∠BAC=15°,∠ACE=∠BCE∠ACB=45°,
∴∠EFA=∠DAC+∠ACE=15°+45°=60°.
故答案为:60°;
(2)证明:∵F是角平分线交点,
∴BF也是角平分线,
∴MF=NF,∠DMF=∠ENF=90°,
在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=∠BAD∠BAC=15°,
∴∠CDA=75°,
∵∠EFA=60°,∠BAD=15°,
∴∠NEF=75°=∠MDF,
在△DMF和△ENF中,
,
∴△DMF≌△ENF(AAS),
∴EF=DF.
(3)解:作FH⊥AC于H,
∵CE是∠BCA的平分线,
∴FH=FM,
∵∠ACB=90°,∠BAC=30°,
∴BCAB=10,AC=10,
设到的距离为,到的距离为,
在的角平分线上
,
设CD=x,则
∴CD=.
【点评】本题主要考查角平分线的性质和全等三角形的判定和性质,三角形内角和定理,证明△EFN≌△DFM是解题的关键.
26. 【分析】(1)先求出点A、B、C坐标,再利用待定系数法将A、C坐标代入求解a、c值即可解答;
(2)设点P(x,),则E(x,),由得到x的方程,解方程即可解答;
(3)求出K(2,0),设N(n,),M(m,),利用待定系数法分别求出直线KN、KM的解析式,进而得到H、G的坐标,则可由m、n表示出OH·OG,再设直线MN的解析式为,与抛物线联立方程组,利用一元二次方程的根与系数关系求得m+n,mn,进而可得出OH·OG=,再根据题目要求求得t值即可.
解:(1)将y=0代入中得:x=-4,
∴A(-4,0),
将x=0代入中得:y=2,
∴B(0,2),
∴CB=OB=2,则OC=4,
∴C(0,4),
将A(-4,0)、C(0,4)代入中,得
,解得:,
∴该抛物线的解析式为;
(2)设点P(x,),则E(x,),F(x,0),
∴PE=-()=,EF=,
∵PE=2EF,
∴=2(),即,
解得:x=-1或x=-4(舍去),
将x=-1代入中得:y=,
∴点P的坐标为(-1,);
(3)存在.
将y=0代入中,解得x=2或x=-4(舍去),
∴K(2,0),
设N(n,),M(m,),
设直线KN的解析式为y=k(x-2),
将点N坐标代入,得:k= ,
∴直线KN的解析式为,
当x=0时,y=n+4,∴OH=n+4,
设直线KM的解析式为y=b(x-2),
将点M坐标代入,得:b= ,
∴直线KM的解析式为,
当x=0时,y=m+4,
∴OG=-m-4,
∴OH·OG=(n+4)(-m-4)=-mn-4(m+n)-16,
∵直线MN过点T(t,-1),且与抛物线交于M、N两点,
∴设直线MN的解析式为y=e(x-t)-1,代入中,
得:,
∴m+n=-(2e+2),mn=-2et-10,
∴OH·OG=2et+10+8e+8-16=2e(t+4)+2,
∴当t+4=0即t=-4时,OH·OG=2(定值),
即存在t=-4,使得OG与OH的积为定值2.
【点评】本题考查二次函数的综合应用,涉及待定系数法求函数解析式、函数图象上点的坐标特征、坐标与图形性质、函数图象与坐标轴的交点问题、二次函数与一元二次方程的关系等知识,综合性强,难度较难,解答的关键是理解题意,借助数形结合思想找寻各知识点的联系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2023】湖南省娄底市中考数学模拟试卷3
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一个选项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.下列说法正确的是( )
A.倒数等于他本身的数只有1 B.平方等于他本身的数只有1和0
C.立方等于他本身的数只有1 D.绝对值等于他本身的数只有正数
2.在下列各式的计算中,正确的是( )
A. B.
C. D.
3.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩(分) 80 85 90 95
人数(人) 1 2 5 2
则这组数据的中位数和众数分别为( )
A.90,89 B.90,90 C.90,90.5 D.9
4.下面图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
5.据中国互联网络信息中心(CNNIC)在京发布的《中国互联网络发展状况统计报告》,截至2019年6月底,我国4G手机用户数达到5.74亿户,将5.74亿这个数用科学记数法可表示为( )
A. B. C. D.
6.如图,直线a,b相交于点O,若,则等于( )
A. B. C. D.
7.将不等式组的解集表示在数轴上,下列表示正确的是( )
A. B.
C. D.
8.某个一次函数的图象与直线平行,并且经过点,则这个一次函数的解析式为( )
A. B. C. D.
9.一次函数y=kx+b的图象与y轴的交点的纵坐标为-5,且当x=1时,y=-2,那么这个函数的表达式是( )
A.y=4x-6 B.y=-3x-5 C.y=3x+5 D.y=3x-5
10.观察下列等式:,,,,,,…,根据其中的规律可得的结果的个位数字是( )
A. B. C. D.
11.如图,△AOB和△ACD均为正三角形,且顶点B、D均在双曲线(x>0)上,连接BC交AD于P,连接OP,则图中是( )
A. B.3 C.6 D.12
12.定义:如果(,且),那么x叫做以a为底N的对数,记做.例如:因为,所以;因为,所以.下列说法:①;②;③若,则;④;正确的序号有( )
A.①③ B.②③ C.①②③ D.②③④
二、填空题(本大题共6小题,每小题3分,满分18分)
13.若有意义,则的取值范围是_________.
14.若关于的一元二次方程的一个根是,则另一个根是_____________________.
15.口袋里有大小相同的8个红球、4个白球和4个黄球,从中任意摸出1个球,摸出红球的可能性是____.
16.如图,已知中,,,将绕点A顺时针方向旋转60°到的位置,连接,则点到BC的距离为______.
17.如图,点P为线段AB上的一个动点,AB=6,以PA、PB为边向同侧作正方形APDC、正方形PBEF,两正方形的对角线的交点分别记为O1、O2,连接O1O2,则O1O2的最小值为_____.
18.如图,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,把一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B.梦想飞扬学习小组将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,给出下列结论:①线段AE与AF的长度之和为定值;②∠BEO与∠OFC的度数之和为定值;③四边形AEOF的面积为定值.其中正确的是:_______________.(填序号)
三、解答题(本大题共2小题,每小题6分,共12分)
19.(1)计算:;
(2)化简:.
20.先化简,再求值:,其中x是不等式的最大整数解.
四、解答题(本大题共2小题,每小题8分,共16分)
21.奉节脐橙丰收了,某镇为帮助果农扩大销量,利用网络平台直播带货进行销售.为了解平台在一个季度内每天的销售额,从中随机抽取了20天的销售额(单位:万元)作为样本,数据如下:
15,14,15,15,14,16,12,13,13,16,16,14,13,17,15,14,16,17,14,14
(1)根据上述样本数据,补全条形统计图;
(2)上述样本数据的众数是____________万元,中位数是_____________万元;
(3)该网络平台一共有两男两女四名主播,每天随机有两名主播进行直播带货,请用树状图或者列表的方法求出某一天刚好主播是一男一女的概率是多少?
22.由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用.
(1)求出线段OA和双曲线函数表达式;
(2)从消毒开始,至少在多少分钟内,师生不能待在教室?
五、解答题(本大题共2小题,每小题9分,共18分)
23.森泽家买了一套住房有三个卧室,其中A卧室的地面面积为,B卧室的地面面积为,设C卧室地面面积的数值为m,且;
(1)求m的值(用含有x、y的式子表示);
(2)森泽想把所有卧室的地面都铺上地砖,恰好每平方米地砖费用也是40元,且满足:m比x大10,y是最小的正整数,求铺地砖的总费用是多少元?
(3)在(2)的条件下,森泽想把墙面也铺上壁纸,已知墙面的总面积比地面总面积5倍多15平方单位,某厂家有两个车间可以生产这批壁纸,其中,第二车间比第一车间人数的少3人,如果从第二车间调出10人到第一车间,那么第二车间的人数是第一车间人数的一半,两个车间的每位工人每天可以生产0.5平方单位壁纸,若第一车间和第二车间共同为森泽家生产这批壁纸,几天可以完工?
24.如图,△ABC内接于, AB为直径,∠ACB 的平分线分别交AB于点D.交于点E,过点E作的切线,交CE的平行线AF于点F.
(1)求证:四边形ADEF为平行四边形.
(2)若tan∠CAB=,AF=5,求四边形ADEF的面积.
六、综合题(本大题共2小题,每小题10分,共20分)
25.综合与实践,如图,在Rt△ABC中,,,AD、CE分别是∠BAC、∠BCA的平分线,AD与CE相交于点F,交BC于点M,交AB于点N,连接BF.
(1)∠EFA的度数为 .
(2)求证:.
(3)若,求CD的长.
26.如图,直线交x轴于点A,交y轴于点B,点C在y轴上,,经过点A,C的抛物线交直线AB于另一点D.
(1)求抛物线的解析式;
(2)点P为直线AB上方抛物线上一点,过点P作轴于点F,交AB于点E.当时,求点P的坐标;
(3)抛物线与x轴的另一个交点为K,过点的任意直线MN(不与y轴平行)与抛物线交于点M,N,直线KM,KN分别交y轴于点G,H,是否存在t的值使得OG与OH的积为定值?若存在,求t的值,若不存在,请说明理由.
参考答案:
1.【分析】根据倒数、平方、立方、绝对值的概念对各选项逐一判断即可得出答案.
解:A.倒数等于他本身的数有、,故此选项不符合题意;
B.平方等于他本身的数有、,故此选项符合题意;
C.立方等于他本身的数有、、,故此选项不符合题意;
D.绝对值等于他本身的数有和正数,故此选项不符合题意.
故选:B.
【点评】本题考查倒数、平方、立方、绝对值的概念.理解和掌握相关的概念是解题的关键.
2.【分析】利用合并同类项的法则以及积的乘方、幂的乘方,平方差公式即可判断.
解:A. 不是同类项,不能合并,故选项错误;
B. ,选项正确;
C. ,故选项错误;
D. ,故选项错误.
故选:B.
【点评】本题考查幂的乘方与积的乘方,平方差公式,单项式乘多项式,合并同类项,解题关键在于掌握运算法则.
3.【分析】先把这些数从小到大排列,根据众数及中位数的定义求出众数和中位数.
解:在这一组数据中90是出现次数最多的,故众数是90,
而将这组数据从小到大的顺序排列后,处于中间位置的那个数是90、90,
那么由中位数的定义可知,这组数据的中位数是90.
故选:B.
【点评】本题主要考查众数与中位数,众数是一组数据中出现次数最多的数,中位数是将一组数据从小到大(或从大到小)重新排列后,若有奇数个数据,最中间的那个数,若有偶数个数据,最中间两个数的平均数,叫做这组数据的中位数,掌握众数和中位数的定义是解题的关键.
4.【分析】根据轴对称图形的定义和中心对称图形的定义对每个选项进行判断即可.
解:A项是轴对称图形,不是中心对称图形;
B项是中心对称图形,不是轴对称图形;
C项是中心对称图形,不是轴对称图形;
D项是中心对称图形,也是轴对称图形;
故选:D.
【点评】本题考查了轴对称图形的定义和中心对称图形的定义,掌握知识点是解题关键.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
5.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
解:5.74亿用科学记数法表示为:.
故答案为:.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
6.【分析】根据对顶角相等可得,再由邻补角的定义即可求解.
解:∵,
∴,
∴,
故选:C.
【点评】本题主要考查了对顶角相等,解题的关键是正确掌握对顶角的性质和邻补角的定义.
7.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:由x+4>4,得:x>0,
由1-2x>-1,得:x<1,
则不等式组的解集为0<x<1,
在数轴上表示为
故选:B.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
8.【分析】根据两直线平行时k的值相等,设出所求解析式,把已知点坐标代入计算即可.
解:由一次函数的图象与直线y═x+6平行,设直线解析式为y=x+b,
把( 2, 4)代入得: 4= 1+b,即b= 3,
则这个一次函数解析式为y=x 3.
故选:C.
【点评】此题考查了待定系数法求一次函数解析式,以及一次函数的图象,熟练掌握待定系数法是解本题的关键.
9.【分析】根据题意,先把(1,-2)、(0,-5)代入y=kx+b中,得到关于k、b的二元一次方程组,然后解方程组即可.
解:把(1,-2)、(0,-5)代入y=kx+b中,
得,
解得.
故一次函数的解析式是y=3x-5.
故选D.
【点评】本题考查了待定系数法求一次函数解析式,解题的关键是掌握y轴上点的横坐标为0及二元一次方程组的解法.
10.【分析】由已知可得尾数,,,的规律是4个数一循环,则的结果的个位数字与的个位数字相同,即可求解.
解:∵,,,,,,…,
∴尾数,,,的规律是4个数一循环,
∵,
∴的个位数字是,
又∵,
∴的结果的个位数字与的个位数字相同,
∴的结果的个位数字是.
故选:A.
【点评】本题考查数的尾数特征,能够通过所给数的特点,确定尾数的循环规律是解题的关键.
11.【分析】先根据△AOB和△ACD均为正三角形可知,故可得出ADOB,所以,故,过点B作BE⊥OA于点E,由反比例函数系数k的几何意义即可得出结论.
解:如图:
∵△AOB和△ACD均为正三角形,
∴,
∴ADOB,
∴,
∴,
过点B作BE⊥OA于点E,则,
∵点B在反比例函数的图象上,
∴,
∴.
故选:C.
【点评】本题考查的是反比例函数,等边三角形的性质及反比例函数系数k的几何意义等知识,综合运用以上知识是解题的关键.
12.【分析】由新定义可得:利用新定义逐一计算判断,从而可得答案.
解:根据新定义可得: 故①不符合题意;
故②符合题意;
,
解得: 故③符合题意;
,故④符合题意,
故选D
【点评】本题考查的新定义运算,有理数的乘方运算的含义,正确理解新定义,运用新定义解决问题是解本题的关键.
13.【分析】根据二次根式有意义的条件,被开方数大于等于0,以及分母不等于0,即可求的取值范围.
解:根据题意得:,,
解得且.
故答案为:且.
【点评】主要考查了二次根式以及分式有意义的条件.解题的关键是二次根式中的被开方数必须是非负数,否则二次根式无意义;分式有意义的条件是分母不等于零.
14.【分析】根据根与系数的关系计算即可.
解:设另一个根为,则,解得
故答案为
【点评】本题考查一元二次方程根与系数的关系,熟记公式是解题的关键,也可以把代入方程求出k的值再解方程.
15.【分析】根据红球的个数÷总个数=摸出红球的可能性即可得出答案.
解:8+4+4=16(个),
,
故摸到红球的可能性是.
故答案为.
【点评】本题考查简单概率计算.对于这类题目,看红球被摸到的可能性是几分之几,就看红球占总数的几分之几就可以了.
16.【分析】过点作E⊥AC于E,D⊥BC于D,得到四边形DCE是矩形,由∠AC=60°,得到∠AE=30°,求出AE,由此求出答案.
解:过点作E⊥AC于E,D⊥BC于D,
∵,
∴四边形DCE是矩形,
∵A=AC=,∠AC=60°,
∴∠AE=30°,
∴,
∴D=CE=-=,
故答案为:.
【点评】此题考查旋转的性质,矩形的判定定理及性质定理,直角三角形30度角的性质,熟记矩形的判定及旋转的性质是解题的关键.
17.【分析】作O1M⊥AP于M,O2N⊥PB于N,O1Q⊥O2N于Q,如图,利用正方形的性质得△AO1P和△PO2B都是等腰直角三角形,则AM=PM,PN=BN,所以MN=AB=3,再证明四边形O1MNO2为矩形得到O1Q=MN=3,然后根据垂线段最短得到O1O2的最小值.
解:作O1M⊥AP于M,O2N⊥PB于N,O1Q⊥O2N于Q,如图,
∵四边形APDC和四边形PBEF都为正方形,
,
∴△AO1P和△PO2B都是等腰直角三角形,
∵O1M⊥AP,O2N⊥PB,
∴AM=PM,PN=BN,
∴MN=PM+PN=AB=3,
∵O1M⊥AP,O2N⊥PB,O1Q⊥O2N,
,
∴四边形O1MNO2为矩形,
∴O1Q=MN=3,
∵O1O2≥O1Q,
∴O1O2的最小值为3.
故答案为:3.
【点评】本题主要考查正方形的性质,等腰三角形的性质,垂线段最短,掌握正方形的性质,等腰三角形的性质,垂线段最短是解题的关键.
18.【分析】连接,先证,利用全等三角形的性质可得出,进而可得出,结论①正确;由三角形的内角和定理、结合,可得,结论②正确;由可得出,结合图形可得出,结论③正确.
解:如图,连接,
为等腰直角三角形,点为的中点,
,,.
,,
.
在和中,,
,
,
,则结论①正确;
,,,
,则结论②正确;
,
,
,则结论③正确;
综上,正确的结论是①②③,
故答案为:①②③.
【点评】本题考查了三角形全等的判定定理与性质、等腰直角三角形等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.
19.【分析】(1)先算乘方、绝对值和特殊三角函数值,再算加减法即可.
(2)根据完全平方公式和平方差公式化简式子,再合并同类项即可.
解:(1)
.
(2)
.
【点评】本题考查了实数的混合运算和化简多项式的问题,掌握实数混合运算法则、绝对值的性质、特殊三角函数值、完全平方公式、平方差公式是解题的关键.
20.【分析】先化简分式,再求出不等式的解集,确定x的值即可.
解:
解不等式,得不等式的解集:
∴最大整数解:
当时,
原式.
【点评】本题主要考查了分式的化简求值与一元一次不等式的整数解,解题的关键是能够正确的化简分式和求出一元一次不等式的整数解.
21.【分析】(1)根据题目中的数据,可以得到销售额14万元和16万元的天数,然后即可将条形统计图补充完整;
(2)根据条形统计图中的数据,可以直接写出样本数据的众数,计算出样本数据的中位数;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到一男和一女的情况,再利用概率公式即可求得答案.
解:(1)由题目中的数据可得,
销售额为14万元的有6天,销售额为16万元的有4天,
补全的条形统计图如右图所示;
(2)由条形统计图可得,
样本数据的众数是14万元,中位数是(万元),
故答案为:14,14.5;
(3)画树状图得:
∵共有12种等可能的结果,抽取的两人恰好是一男和一女的有8种结果,
∴抽取的两人恰好是一男和一女的概率为.
【点评】本题考查条形统计图、中位数、众数、树状图法与列表法求概率,解答本题的关键是明确条形统计图的特点,会计算一组数据的中位数和加权平均数.用到的知识点为:概率=所求情况数与总情况数之比.
22.【分析】(1)先求解反比例函数解析式,再求解当时,的值,再求解段的解析式,从而可得答案;
(2)分别求解当时,的值,再结合函数图象可得答案.
解:(1)设反比例函数为:
把代入得:
当时,
设段为:
把代入得: 则
段为:
(2)如图,直线与函数图象交于两点,
把代入得:
把代入得:
所以从消毒开始,至少在分钟内,师生不能待在教室.
【点评】本题考查的是正比例函数与反比例函数的实际应用,利用待定系数法求解正比例与反比例函数的解析式,以及正比例与反比例图象上的点的坐标特点,掌握以上知识是解题的关键.
23.【分析】(1)由代入A、B进行整式的加减运算,注意括号、负号的作用;
(2)由y为最小正整数,得到,由m比x大10,得到,继而解得,,再解得铺地砖的总费用,代入数值解题即可;
(3)设第一车间人数为x人,则第二车间人数人,根据题意列方程,解方程即可求出x,进一步即可求出结果.
解:(1)
答:m值为.
(2)∵y为最小正整数,∴,
∵m比x大10,∴
当,时,
(元)
答:总费用为5760元
(3)设第一车间人数为x人,则第二车间人数人.
(人)
(平方单位)
(平方单位)
天
答:14天可以完工.
【点评】本题考查整式的加减、整式的化简求值、一元一次方程的实际应用等知识,是重要考点,掌握相关知识是解题关键.
24.【分析】(1)连接OE,由AB为直径可得,由CE平分可得,利用同弧所对的圆心角是圆周角的2倍,可得,由EF为的切线,可得,根据同旁内角互补,两直线平行,可得,又因为,即可得出结论;
(2)过点A作交CE于点G,利用相似三角形的判定与性质,以及勾股定理,即可求解.
(1)证明:连接OE,如图,
∵AB为直径,
∴,
∵CE平分,
∴,
∴,
∵EF为的切线,
∴,
∵,
∴,
∵,即,
∴四边形ADEF为平行四边形;
(2)解:过点A作交CE于点G,如图,
∵tan∠CAB=,
∴,
设,
,
,
∵,,
,
,
,
在和中,
,
,
,
,
,
∵四边形ADEF为平行四边形,AF=5,
,
,
,
,
,
,
解得,
(舍去),
.
【点评】本题主要考查了圆周角定理、角平分线的定义、平行四边形的判定、勾股定理与相似三角形的判定与性质.
25.【分析】(1)根据角平分线的定义得∠DAC=∠BAD∠BAC=15°,∠ACE=∠BCE∠ACB=45°,根据三角形外角的性质即可求解;
(2)根据条件可得到FM=FN,再根据角的度数可求得∠FDC=75°=∠FEN,可证明△EFN≌△DFM,可得到EF=DF.
(3)作FH⊥AC于H,根据角平分线的性质可得,根据,可得,即可求解.
解:(1)在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠DAC=∠BAD∠BAC=15°,∠ACE=∠BCE∠ACB=45°,
∴∠EFA=∠DAC+∠ACE=15°+45°=60°.
故答案为:60°;
(2)证明:∵F是角平分线交点,
∴BF也是角平分线,
∴MF=NF,∠DMF=∠ENF=90°,
在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=∠BAD∠BAC=15°,
∴∠CDA=75°,
∵∠EFA=60°,∠BAD=15°,
∴∠NEF=75°=∠MDF,
在△DMF和△ENF中,
,
∴△DMF≌△ENF(AAS),
∴EF=DF.
(3)解:作FH⊥AC于H,
∵CE是∠BCA的平分线,
∴FH=FM,
∵∠ACB=90°,∠BAC=30°,
∴BCAB=10,AC=10,
设到的距离为,到的距离为,
在的角平分线上
,
设CD=x,则
∴CD=.
【点评】本题主要考查角平分线的性质和全等三角形的判定和性质,三角形内角和定理,证明△EFN≌△DFM是解题的关键.
26. 【分析】(1)先求出点A、B、C坐标,再利用待定系数法将A、C坐标代入求解a、c值即可解答;
(2)设点P(x,),则E(x,),由得到x的方程,解方程即可解答;
(3)求出K(2,0),设N(n,),M(m,),利用待定系数法分别求出直线KN、KM的解析式,进而得到H、G的坐标,则可由m、n表示出OH·OG,再设直线MN的解析式为,与抛物线联立方程组,利用一元二次方程的根与系数关系求得m+n,mn,进而可得出OH·OG=,再根据题目要求求得t值即可.
解:(1)将y=0代入中得:x=-4,
∴A(-4,0),
将x=0代入中得:y=2,
∴B(0,2),
∴CB=OB=2,则OC=4,
∴C(0,4),
将A(-4,0)、C(0,4)代入中,得
,解得:,
∴该抛物线的解析式为;
(2)设点P(x,),则E(x,),F(x,0),
∴PE=-()=,EF=,
∵PE=2EF,
∴=2(),即,
解得:x=-1或x=-4(舍去),
将x=-1代入中得:y=,
∴点P的坐标为(-1,);
(3)存在.
将y=0代入中,解得x=2或x=-4(舍去),
∴K(2,0),
设N(n,),M(m,),
设直线KN的解析式为y=k(x-2),
将点N坐标代入,得:k= ,
∴直线KN的解析式为,
当x=0时,y=n+4,∴OH=n+4,
设直线KM的解析式为y=b(x-2),
将点M坐标代入,得:b= ,
∴直线KM的解析式为,
当x=0时,y=m+4,
∴OG=-m-4,
∴OH·OG=(n+4)(-m-4)=-mn-4(m+n)-16,
∵直线MN过点T(t,-1),且与抛物线交于M、N两点,
∴设直线MN的解析式为y=e(x-t)-1,代入中,
得:,
∴m+n=-(2e+2),mn=-2et-10,
∴OH·OG=2et+10+8e+8-16=2e(t+4)+2,
∴当t+4=0即t=-4时,OH·OG=2(定值),
即存在t=-4,使得OG与OH的积为定值2.
【点评】本题考查二次函数的综合应用,涉及待定系数法求函数解析式、函数图象上点的坐标特征、坐标与图形性质、函数图象与坐标轴的交点问题、二次函数与一元二次方程的关系等知识,综合性强,难度较难,解答的关键是理解题意,借助数形结合思想找寻各知识点的联系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
