人教版数学八年级下册18.2.1 矩形 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.1 矩形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 00:00:00 | ||
图片预览



文档简介
18.2.1 矩形 同步练习
一、单选题
1.如图,公路,互相垂直,公路的中点与点被湖隔开,若测得的长为,则,两点间的距离为( )
A. B. C. D.
2.如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
A.4 B.6 C.8 D.
3.平行四边形、矩形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
4.求证:直角三角形斜边上中线等于斜边的一半.
已知:如图,在中,,点是的中点.求证:.
证明:延长到,使,
连接、
中间的证明过程排乱了:
①∵
②∵,;
③∴四边形是平行四边形;
④∴四边形是矩形.
∴,∴.
则中间证明过程正确的顺序是( ).
A.①④②③ B.①③②④ C.②④①③ D.②③①④
5.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
6.如图,E、F分别为矩形ABCD边AB、AD上的两点,BE、DF相交于G点,且BE=FD,∠FGB=19°,则∠BGC=( )
A.71° B.80.5° C.81° D.71.5°
7.中,,D为边的中点,则的长度是( )
A.4.5 B.5.5 C.6.5 D.7.5
8.如图,四边形的对角线互相平分,以下添加的条件不能判定四边形是矩形的是( )
A. B.
C. D.
9.如图,将矩形沿对角线所在直线折叠,使点落在点处,交于点,,,则长为( )
A.4 B.5 C.6 D.7
10.将矩形纸片ABCD对折, 使点B与点D重合,折痕为EF,连结BE,则与线段BE相等的线段条数(不包括BE,不添加辅助线)有 ( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,四边形ABCD的对角线AC、BD交于点O,且AB=CD,∠ABD=∠CDB,请再添加一个条件,使四边形ABCD是矩形,你添加的条件是_________.(写出一种即可)
12.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且AF= 5cm,求DE的长度.
13.如图,中,,, 分别是的中位线和中线,,则______.
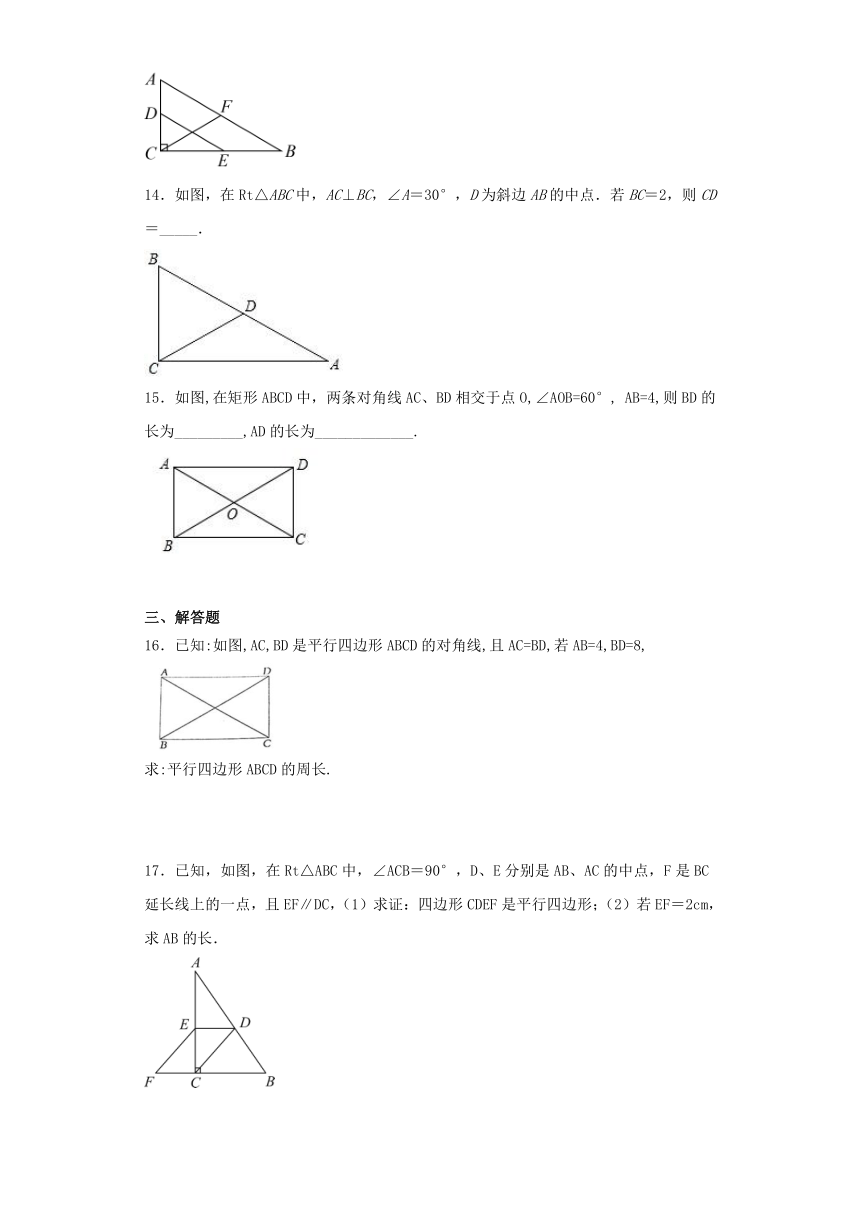
14.如图,在Rt△ABC中,AC⊥BC,∠A=30°,D为斜边AB的中点.若BC=2,则CD=_____.
15.如图,在矩形ABCD中,两条对角线AC、BD相交于点O,∠AOB=60°, AB=4,则BD的长为_________,AD的长为_____________.
三、解答题
16.已知:如图,AC,BD是平行四边形ABCD的对角线,且AC=BD,若AB=4,BD=8,
求:平行四边形ABCD的周长.
17.已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC,(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
18.如图,在四边形ABCD中,AD∥BC,∠A=∠C=90°,点E、F分别在AB、DC上,连接DE,BF,若AE=CF;求证:DE=BF.
19.如图,在中,,,,于点是的中点,求的长.
20.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE∥BC,DE∥AB.
证明:(1)AE=DC;
(2)四边形ADCE为矩形.
参考答案
1.B
2.D
3.A
4.D
5.C
6.B
7.C
8.C
9.B
10.B
11.∠ABC=90°
12.5
13.
14.2
15. 8 4
16.平行四边形ABCD的周长为.
17. 【详解】(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC= AB,
∴AB=2DC=4cm.
故答案为(1)见解析;(2)4cm.
18. 【详解】证明:∵AD∥BC,
∴∠ADC+∠C=180°,
∵∠C=90°,
∴∠ADC=90°,
∵∠A=∠C=90°,
∴四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴AB-AE=CD-CF,即BE=DF,
∵AB∥CD,
∴四边形EDFB为平行四边形,
∴DE=BF.
19.
【详解】解:∵,,
∴,,
设,则,
由勾股定理得:,解得:,即,,
∵是的中点,
∴,
∴是等边三角形,
∵,
∴.
20.【详解】解:(1)在△ABC中,∵AB=AC,AD⊥BC,
∴BD=DC,
∵AE∥BC,DE∥AB,
∴四边形ABDE为平行四边形,
∴BD=AE,
∵BD=DC,
∴AE=DC.
(2)∵AE∥BC,AE=DC,
∴四边形ADCE为平行四边形.
又∵AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE为矩形.
一、单选题
1.如图,公路,互相垂直,公路的中点与点被湖隔开,若测得的长为,则,两点间的距离为( )
A. B. C. D.
2.如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
A.4 B.6 C.8 D.
3.平行四边形、矩形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
4.求证:直角三角形斜边上中线等于斜边的一半.
已知:如图,在中,,点是的中点.求证:.
证明:延长到,使,
连接、
中间的证明过程排乱了:
①∵
②∵,;
③∴四边形是平行四边形;
④∴四边形是矩形.
∴,∴.
则中间证明过程正确的顺序是( ).
A.①④②③ B.①③②④ C.②④①③ D.②③①④
5.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
6.如图,E、F分别为矩形ABCD边AB、AD上的两点,BE、DF相交于G点,且BE=FD,∠FGB=19°,则∠BGC=( )
A.71° B.80.5° C.81° D.71.5°
7.中,,D为边的中点,则的长度是( )
A.4.5 B.5.5 C.6.5 D.7.5
8.如图,四边形的对角线互相平分,以下添加的条件不能判定四边形是矩形的是( )
A. B.
C. D.
9.如图,将矩形沿对角线所在直线折叠,使点落在点处,交于点,,,则长为( )
A.4 B.5 C.6 D.7
10.将矩形纸片ABCD对折, 使点B与点D重合,折痕为EF,连结BE,则与线段BE相等的线段条数(不包括BE,不添加辅助线)有 ( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,四边形ABCD的对角线AC、BD交于点O,且AB=CD,∠ABD=∠CDB,请再添加一个条件,使四边形ABCD是矩形,你添加的条件是_________.(写出一种即可)
12.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且AF= 5cm,求DE的长度.
13.如图,中,,, 分别是的中位线和中线,,则______.
14.如图,在Rt△ABC中,AC⊥BC,∠A=30°,D为斜边AB的中点.若BC=2,则CD=_____.
15.如图,在矩形ABCD中,两条对角线AC、BD相交于点O,∠AOB=60°, AB=4,则BD的长为_________,AD的长为_____________.
三、解答题
16.已知:如图,AC,BD是平行四边形ABCD的对角线,且AC=BD,若AB=4,BD=8,
求:平行四边形ABCD的周长.
17.已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC,(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
18.如图,在四边形ABCD中,AD∥BC,∠A=∠C=90°,点E、F分别在AB、DC上,连接DE,BF,若AE=CF;求证:DE=BF.
19.如图,在中,,,,于点是的中点,求的长.
20.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE∥BC,DE∥AB.
证明:(1)AE=DC;
(2)四边形ADCE为矩形.
参考答案
1.B
2.D
3.A
4.D
5.C
6.B
7.C
8.C
9.B
10.B
11.∠ABC=90°
12.5
13.
14.2
15. 8 4
16.平行四边形ABCD的周长为.
17. 【详解】(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC= AB,
∴AB=2DC=4cm.
故答案为(1)见解析;(2)4cm.
18. 【详解】证明:∵AD∥BC,
∴∠ADC+∠C=180°,
∵∠C=90°,
∴∠ADC=90°,
∵∠A=∠C=90°,
∴四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴AB-AE=CD-CF,即BE=DF,
∵AB∥CD,
∴四边形EDFB为平行四边形,
∴DE=BF.
19.
【详解】解:∵,,
∴,,
设,则,
由勾股定理得:,解得:,即,,
∵是的中点,
∴,
∴是等边三角形,
∵,
∴.
20.【详解】解:(1)在△ABC中,∵AB=AC,AD⊥BC,
∴BD=DC,
∵AE∥BC,DE∥AB,
∴四边形ABDE为平行四边形,
∴BD=AE,
∵BD=DC,
∴AE=DC.
(2)∵AE∥BC,AE=DC,
∴四边形ADCE为平行四边形.
又∵AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE为矩形.
