8.3长方体中棱与棱位置关系的认识 课件(21张PPT)
文档属性
| 名称 | 8.3长方体中棱与棱位置关系的认识 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第8章长方体的再认识
8.3长方体中棱与棱的位置关系的认识
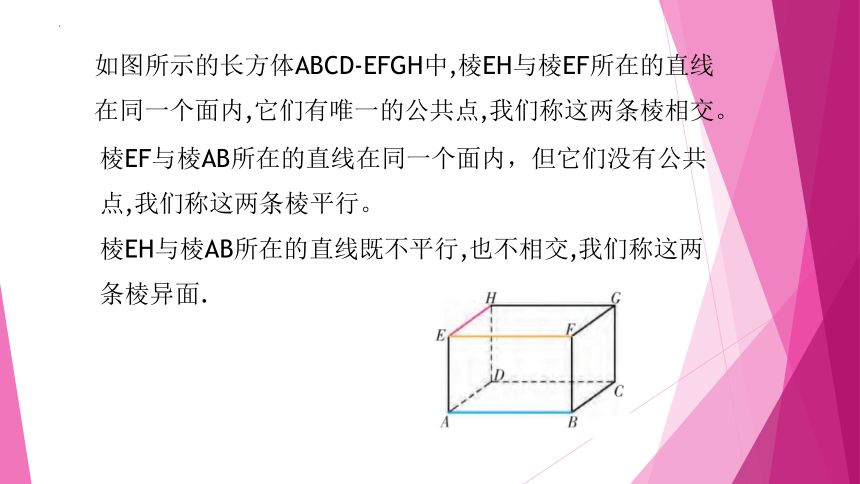
如图所示的长方体ABCD-EFGH中,棱EH与棱EF所在的直线在同一个面内,它们有唯一的公共点,我们称这两条棱相交。
棱EF与棱AB所在的直线在同一个面内,但它们没有公共点,我们称这两条棱平行。
棱EH与棱AB所在的直线既不平行,也不相交,我们称这两条棱异面.
照片中跑道上的任何两条白线互相平行.
照片中铁门的横栏杆与每一根坚栏杆相交,任何两根竖栏杆或横栏杆都是互相平行的。
照片中铁路轨道和公路的位置是异面.
1、相交
2、平行
m
l
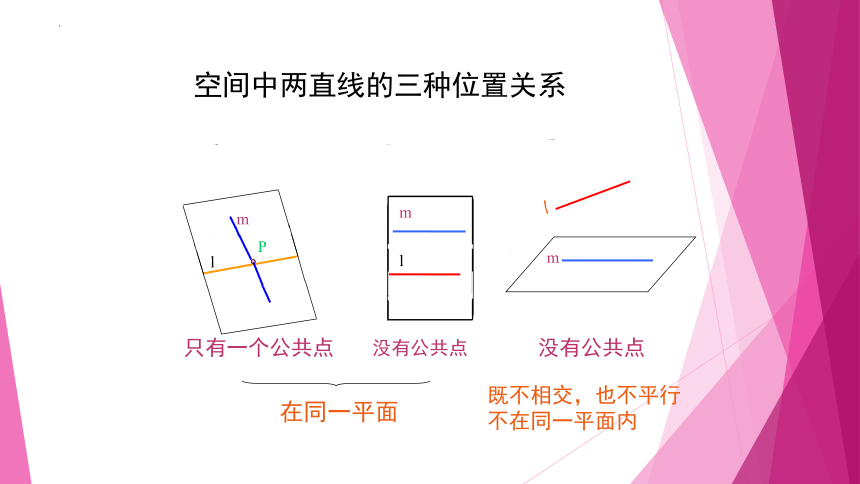
只有一个公共点
没有公共点
在同一平面
空间中两直线的三种位置关系
3、异面直线
没有公共点
既不相交,也不平行
不在同一平面内
m
l
P
α
m
l
一般地,如果直线AB与直线CD在同一平面内,具有唯-公共点,那么称这两条直线的位置关系为相交,读作:直线AB与直线CD相交.
空间两条直线有三种位置关系:相交、平行、异面.
如果直线AB与直线CD在同一平面内,但没有公共点,那么称这两条直线的位置关系为平行,记作:AB//CD,读作:直线AB与直线CD平行。
如果直线AB与直线CD既不平行,也不相交,那么称这两条直线的位置关系为异面,读作:直线AB与直线CD异面
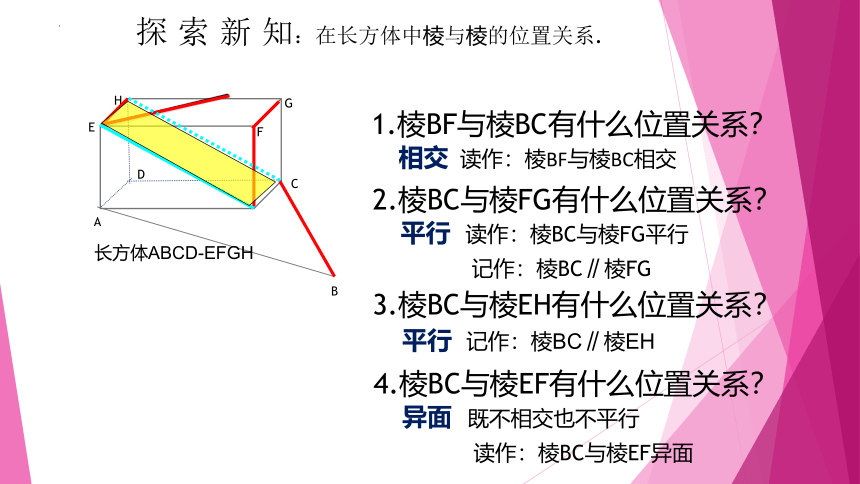
探 索 新 知:在长方体中棱与棱的位置关系.
A
B
C
D
E
F
G
H
1.棱BF与棱BC有什么位置关系?
相交 读作:棱BF与棱BC相交
2.棱BC与棱FG有什么位置关系?
平行 读作:棱BC与棱FG平行
记作:棱BC∥棱FG
3.棱BC与棱EH有什么位置关系?
平行 记作:棱BC∥棱EH
4.棱BC与棱EF有什么位置关系?
异面 既不相交也不平行
读作:棱BC与棱EF异面
长方体ABCD-EFGH
A
C
B
D
F
E
H
G
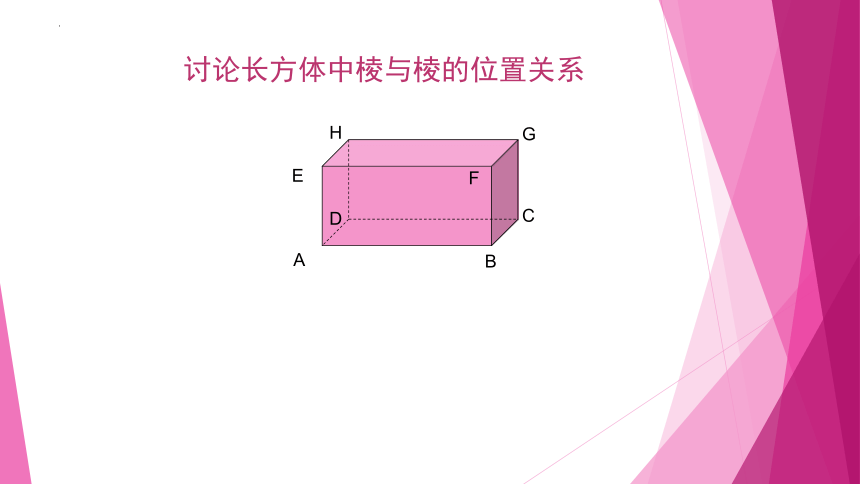
讨论长方体中棱与棱的位置关系
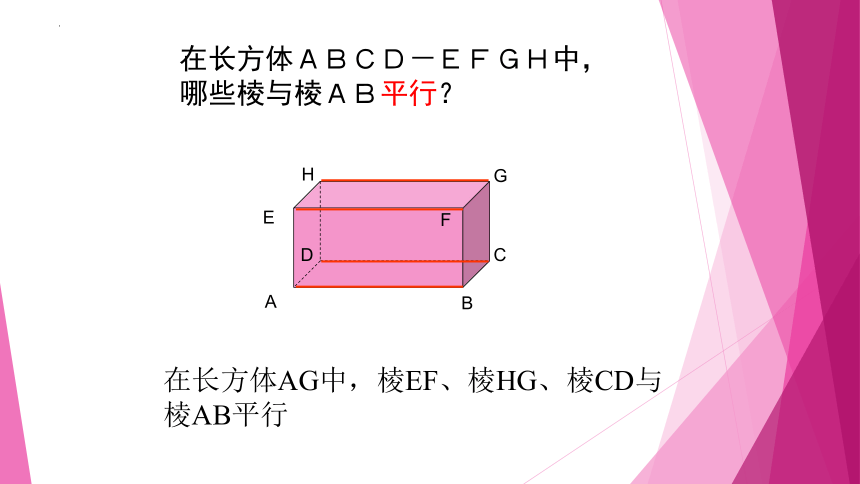
在长方体ABCD-EFGH中,
哪些棱与棱AB平行?
A
C
B
D
F
E
H
G
在长方体AG中,棱EF、棱HG、棱CD与棱AB平行
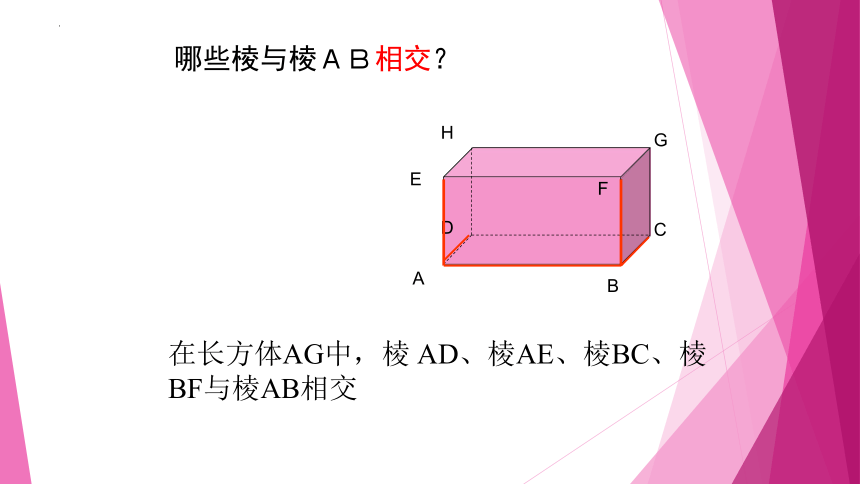
哪些棱与棱AB相交?
A
C
B
D
F
E
H
G
在长方体AG中,棱 AD、棱AE、棱BC、棱BF与棱AB相交
哪些棱与棱AB异面?
A
C
B
D
F
E
H
G
在长方体AG中,棱EH、棱HD、棱FG、棱CG与棱AB异面
例题 在长方体ABCD-EFCH中
(1)哪些棱与棱AB平行
(2)哪些楼与棱AB相交
(3)哪些楼与棱AB异面
解 (1)与棱AB平行的棱有棱EF棱CD与棱GH
(2)与楼AB相交的棱有棱AE棱AD棱BC与棱BF
(3)与棱AB异面的棱有棱EH、棱DH棱FG与棱GC
课本练习
1.用生活实例说明两条直线相交、平行、异面这三种位置关系.
2.长方体ABCD-EFCH中,任意两条棱之间最多有几个公共点 如果两条棱之间没有公共点,那么它们一定异面吗
3.如果把图中建筑物的柱子与屋檐线看成直线,分别用红线与绿线表示.那么两根红线之间及红线与绿线之间的位置关系分别是什么呢
4.在如图所示的大衣柜中,请说出挂衣杆与长方体大衣柜各个面的交线之间的位置关系
随堂检测
一、判断题:
1.如果两条直线没有公共点,则这两条直线一定平行。 ( )
2.如果两条直线有一个公共点,则这两条直线一定相交,并且一定在同一个平面内。 ( )
3.两条直线的位置关系,要么相交,要么平行。 ( )
×
√
×
二、选择题:
1.分别和两条异面直线都相交的两条直线的位置关系是( )
A.异面 B. 相交 C.平行 D.异面或相交
D
2.已知a ,b是异面直线,直线c平行于直线a,那么c与b( )
A. 一定是异面直线 B.一定是相交直线
C. 不可能是平行直线 D.不可能是相交直线
C
1、空间两条不重合的直线的位置关系有________、________、________三种。
2、没有公共点的两条直线可能是________直线,也有可能是________直线。
平行
异面
相交
平行
异面
三.填空:
3.在长方体ABCD-EFGH中,
与棱HD平行的棱有 条?是哪些?
A
C
B
D
F
E
H
G
3
4
4
与棱HD相交的棱有 条?是哪些?
与棱HD异面的棱有 条?是哪些?
四、指出下列各对棱的位置关系:
A
B
C
D
E
F
G
H
⑴棱BC与棱GH
异面
⑵棱AD与棱AE
相交
⑶棱BF与棱DH
平行
⑷棱EF与棱DC
平行
⑸棱BF与棱DC
异面
⑹棱CD与棱CG
相交
A
B
D
C
五、数一数:
长方体ABCD-A1B1C1D1中,有多少对平行的棱?有多少对相交的棱?有多少对异面的棱?
E
F
G
F
有18对平行的棱
有24对相交的棱
有24对异面的棱
课堂小结:
空间两条直线有三种位置关系:
相交、平行、异面。
如果直线AB与直线CD在同一平面内,具有唯一公共点,那么称这两条直线的位置关系为相交,读作:直线AB与直线CD相交。
如果直线AB与直线CD在同一平面内,但没有公共点,那么称这两条直线的位置关系为平行,记作:AB//CD,读作:直线AB与直线CD平行。
如果直线AB与直线CD既不平行,也不相交,那么称这两条直线的位置关系为异面,读作:直线AB与直线CD异面。
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第8章长方体的再认识
8.3长方体中棱与棱的位置关系的认识
如图所示的长方体ABCD-EFGH中,棱EH与棱EF所在的直线在同一个面内,它们有唯一的公共点,我们称这两条棱相交。
棱EF与棱AB所在的直线在同一个面内,但它们没有公共点,我们称这两条棱平行。
棱EH与棱AB所在的直线既不平行,也不相交,我们称这两条棱异面.
照片中跑道上的任何两条白线互相平行.
照片中铁门的横栏杆与每一根坚栏杆相交,任何两根竖栏杆或横栏杆都是互相平行的。
照片中铁路轨道和公路的位置是异面.
1、相交
2、平行
m
l
只有一个公共点
没有公共点
在同一平面
空间中两直线的三种位置关系
3、异面直线
没有公共点
既不相交,也不平行
不在同一平面内
m
l
P
α
m
l
一般地,如果直线AB与直线CD在同一平面内,具有唯-公共点,那么称这两条直线的位置关系为相交,读作:直线AB与直线CD相交.
空间两条直线有三种位置关系:相交、平行、异面.
如果直线AB与直线CD在同一平面内,但没有公共点,那么称这两条直线的位置关系为平行,记作:AB//CD,读作:直线AB与直线CD平行。
如果直线AB与直线CD既不平行,也不相交,那么称这两条直线的位置关系为异面,读作:直线AB与直线CD异面
探 索 新 知:在长方体中棱与棱的位置关系.
A
B
C
D
E
F
G
H
1.棱BF与棱BC有什么位置关系?
相交 读作:棱BF与棱BC相交
2.棱BC与棱FG有什么位置关系?
平行 读作:棱BC与棱FG平行
记作:棱BC∥棱FG
3.棱BC与棱EH有什么位置关系?
平行 记作:棱BC∥棱EH
4.棱BC与棱EF有什么位置关系?
异面 既不相交也不平行
读作:棱BC与棱EF异面
长方体ABCD-EFGH
A
C
B
D
F
E
H
G
讨论长方体中棱与棱的位置关系
在长方体ABCD-EFGH中,
哪些棱与棱AB平行?
A
C
B
D
F
E
H
G
在长方体AG中,棱EF、棱HG、棱CD与棱AB平行
哪些棱与棱AB相交?
A
C
B
D
F
E
H
G
在长方体AG中,棱 AD、棱AE、棱BC、棱BF与棱AB相交
哪些棱与棱AB异面?
A
C
B
D
F
E
H
G
在长方体AG中,棱EH、棱HD、棱FG、棱CG与棱AB异面
例题 在长方体ABCD-EFCH中
(1)哪些棱与棱AB平行
(2)哪些楼与棱AB相交
(3)哪些楼与棱AB异面
解 (1)与棱AB平行的棱有棱EF棱CD与棱GH
(2)与楼AB相交的棱有棱AE棱AD棱BC与棱BF
(3)与棱AB异面的棱有棱EH、棱DH棱FG与棱GC
课本练习
1.用生活实例说明两条直线相交、平行、异面这三种位置关系.
2.长方体ABCD-EFCH中,任意两条棱之间最多有几个公共点 如果两条棱之间没有公共点,那么它们一定异面吗
3.如果把图中建筑物的柱子与屋檐线看成直线,分别用红线与绿线表示.那么两根红线之间及红线与绿线之间的位置关系分别是什么呢
4.在如图所示的大衣柜中,请说出挂衣杆与长方体大衣柜各个面的交线之间的位置关系
随堂检测
一、判断题:
1.如果两条直线没有公共点,则这两条直线一定平行。 ( )
2.如果两条直线有一个公共点,则这两条直线一定相交,并且一定在同一个平面内。 ( )
3.两条直线的位置关系,要么相交,要么平行。 ( )
×
√
×
二、选择题:
1.分别和两条异面直线都相交的两条直线的位置关系是( )
A.异面 B. 相交 C.平行 D.异面或相交
D
2.已知a ,b是异面直线,直线c平行于直线a,那么c与b( )
A. 一定是异面直线 B.一定是相交直线
C. 不可能是平行直线 D.不可能是相交直线
C
1、空间两条不重合的直线的位置关系有________、________、________三种。
2、没有公共点的两条直线可能是________直线,也有可能是________直线。
平行
异面
相交
平行
异面
三.填空:
3.在长方体ABCD-EFGH中,
与棱HD平行的棱有 条?是哪些?
A
C
B
D
F
E
H
G
3
4
4
与棱HD相交的棱有 条?是哪些?
与棱HD异面的棱有 条?是哪些?
四、指出下列各对棱的位置关系:
A
B
C
D
E
F
G
H
⑴棱BC与棱GH
异面
⑵棱AD与棱AE
相交
⑶棱BF与棱DH
平行
⑷棱EF与棱DC
平行
⑸棱BF与棱DC
异面
⑹棱CD与棱CG
相交
A
B
D
C
五、数一数:
长方体ABCD-A1B1C1D1中,有多少对平行的棱?有多少对相交的棱?有多少对异面的棱?
E
F
G
F
有18对平行的棱
有24对相交的棱
有24对异面的棱
课堂小结:
空间两条直线有三种位置关系:
相交、平行、异面。
如果直线AB与直线CD在同一平面内,具有唯一公共点,那么称这两条直线的位置关系为相交,读作:直线AB与直线CD相交。
如果直线AB与直线CD在同一平面内,但没有公共点,那么称这两条直线的位置关系为平行,记作:AB//CD,读作:直线AB与直线CD平行。
如果直线AB与直线CD既不平行,也不相交,那么称这两条直线的位置关系为异面,读作:直线AB与直线CD异面。
