第三章3.1不等关系与不等式课件
图片预览











文档简介
课件63张PPT。3.1不等关系与不等式第一课时长短轻重大小高矮一、不等关系是普遍存在的 现实世界和日常生活中,既有相等关系,又存在着大量的不等关系,如:1、今天的天气预报说:明天早晨最低温度为7℃,明天白天的最高温度为13℃;2、三角形ABC的两边之和大于第三边;3、a是一个非负实数。在数学中,我们怎样来表示这些不等关系?7℃≤t≤13℃AB+AC>BC或……a≥0一、不等关系是普遍存在的自主学习: p72~73, 理解:
1,现实世界中,不等关系是普遍存在的。 2,如何用不等式(组)表示不等关系?
3,怎样比较两个实数的大小? 我们用数学符号“≠”,“>”,“<”,“≥”,“≤”连接两个数或代数式,以表示它们之间的不等关系。含有这些不等号的式子叫做不等式. > ,<是严格不等式;≥,≤是非严格不等式.思考:1、右图是限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h ,写成不等式是:_________402、某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%,用不等式可以表示为:( )v≤40A. f ≥ 2.5%或p ≥ 2.3%B. f ≥ 2.5%且p ≥ 2.3%B自学成果展示:3、中国“神舟七号”宇宙飞船飞天取得了最圆满的成功.我们知道,它的飞行速度( )不小于第一宇宙速度( 记作 ),且小于第二宇宙速度(记作 ).><≥≤≤≥≤≥问题1. 设点A与平面 的距离为d,B为平面
上的任意一点,则ABBBdod≤|AB|.二、用不等式(组)来表示不等关系问题2、某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?思考(1 )销售量减少了多少?
(2)现在销售量是多少?(3)销售总收入为多少?
二、用不等式(组)来表示不等关系问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍 请思考:(1)找出两种规格的钢管的数量满足的不等关系.
(2)用不等式(组)表示上述不等关系.分析:假设截得500mm的钢管x根,截得600mm的钢管y根。根据题意,应当有什么样的不等关系呢?(3)截得两种钢管的数量都不能为负.(2)截得600mm钢管的数量不能超过500mm
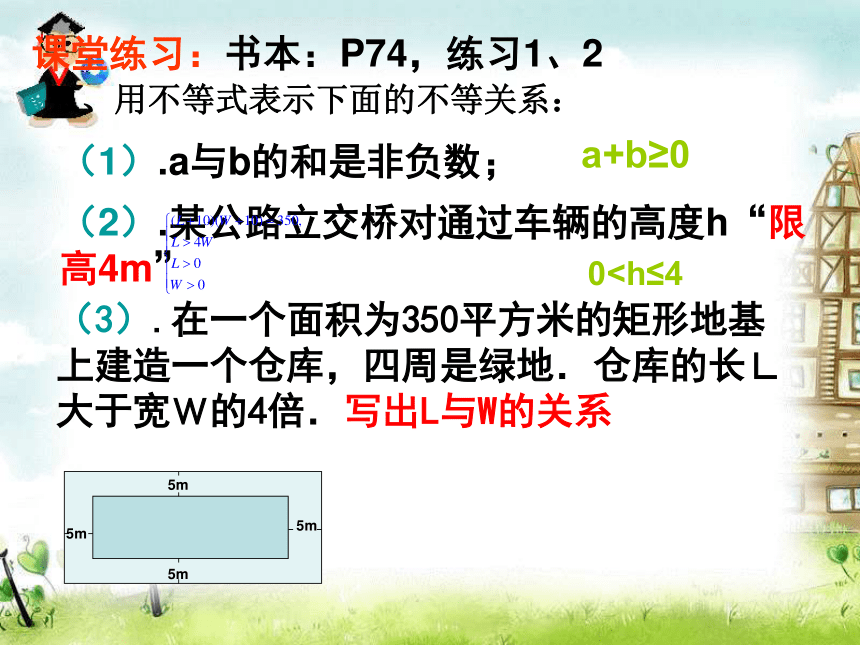
的钢管数量的3倍;(1)截得两种钢管的总长度不能超过4000mm;二、用不等式(组)来表示不等关系上面三个不等关系,是“且”的关系,要同时满足的话,可以用下面的不等式组来表示:考虑到实际问题的意义,还应有x,y∈Nx,y∈N二、用不等式(组)来表示不等关系课堂练习:书本:P74,练习1、2(1).a与b的和是非负数;(2).某公路立交桥对通过车辆的高度h“限高4m”(3).在一个面积为350平方米的矩形地基
上建造一个仓库,四周是绿地.仓库的长L
大于宽W的4倍.写出L与W的关系a+b≥002、有一个两位数大于50而小于60,其个位数字
比十位数字大2,试用不等式(组)表示上述关系1.分析:设个位数字为 , 十位数字为 ,则自主学习: p73,了解比较实数大小的方法作差变形判断结论因式分解、配方、通分等手段三、不等式基本原理例1.比较x2-x与x-2的大小.解:(x2-x)-(x-2)=x2-2x+2 =(x-1)2+1,因为(x-1)2≥0,
所以(x2-x)-(x-2)>0,因此x2-x>x-2.比较两个数(式)的大小的方法:(1)作差(2)变形(3)判号(4)结论小结:作差法的步骤:(1)作差→(2)变形→(3)定号→(4)结论其中,变形的方法有:配方法;因式分解法;分子有理化等。 例2:比较下面两式的大小:
小结:作差法的步骤:
(1)作差→(2)变形→(3)定号→(4)结论其中,变形的方法有:配方法;因式分解法;分子有理化等。配方配方因式分解比较两个数(式)的大小的方法:若b>a,结论又会怎样呢? 例4.
(1)已知a>0且a≠1,
比较p与q的大小;
(2)设a>0,b>0且a≠b,比较aabb与baab的大小.例5.设m.>n>0,a>0且a≠1,试比较am+a-m与an+a-n的大小.
五、小结:1.不等关系是普遍存在的2.用不等式(组)来表示不等关系3.不等式基本原理
4.作差比较法
(1)作差→(2)变形→(3)定号→(4)结论其中,变形的方法有:配方法;因式分解法;分子有理化等。姚明身高>奥尼尔身高生活中,我们可用不等式来表示一些不等关系横看成岭侧成峰
远近高低各不同行车速度 V≤40km/h解:x3-(x2-x+1)=x3-x2+x-1
=x2(x-1)+(x-1)
=(x-1)(x2+1),∵ x2+1>0,
∴ 当x>1时,x3>x2-x+1; 当x=1时,x3=x2-x+1,当x<1时,x3 b,c > d是同向不等式.(2) 异向不等式:两个不等号方向相反的不等式 .例如:a > b,c < d是异向不等式.新课知识探究(二):比较实数大小的基本原理 思考1:实数可以比较大小,对于两个实数a,b,其大小关系有哪几种可能? a>b,a=b,a<b. 思考2:任何一个实数都对应数轴上的一个点,那么大数与小数所对应的点的相对位置关系如何? 大数对应的点位于小数对应的点的右边 思考3:如果两个实数的差是正数,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理? a-b>0 a>b 思考5:如果两个实数的差等于零,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理? a-b=0 a=b 思考4:如果两个实数的差是负数,那么这两个实数的大小关系如何?反之成立吗?如何用数学语言描述这个原理? a-b<0 a<b 两数大小的比较 某人为自己制定的月支出计划中,规定手机费不超过150元,他所选用的中国电信卡的收费标准为:求这个人月通话时间的取值范围。 即:30+0.4x≤150. 解得x≤300.练习1:若需在长为4000mm圆钢上,截出长为698mm和518mm的两种毛坯,问怎样写出满足上述所有不等关系的不等式组?分析:
设698mm与518mm分别x与y个练习2 、一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料需要的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨。现有库存磷酸盐10吨、硝酸盐66吨,在此基础上进行生产。请用不等式组把此实例中的不等关系表示出来。分析:设分别生产甲.乙两种肥料为x吨,y吨练习3、某年夏天,我国遭受特大洪灾,灾区学生小李家中经济发生困难,为帮助小李解决开学费用问题,小李所在班级学生(小李除外)决定承担这笔费用。若每人承担12元人民币,则多余84元;若每人承担10元,则不够;若每人承担11元,又多出40元以上。问该班共有多少人?这笔开学费用共多少元?分析:设该班除小李外共有x人,这笔开学费用共y元,则:变式:如果设杂志的单价提高了0.1n元(n∈N*),如何用不等式表示销售的总收入仍不低于20万元呢?你能计算出n在哪个范围内变化吗?分析:销售量减少了0.2n万本,单价为
(2.5+0.1n)元,则可得到销售的总以收入为不低于20万元的不等式可表示为:
(2.5+0.1n)(8-0.2n)≥20二、用不等式(组)来表示不等关系A 例题讲解 例1 某用户计划购买单价分别为60元、70元的单片软件和盒装磁盘,使用资金不超过500元,根据需要,软件至少买3片,磁盘至少买2盒,用不等式组表示软件数x与磁盘数y应满足的条件. 例2 比较下列三组代数式的大小: (1)x2+3与3x; (2) x6+1与x4+x2;(3)例题讲解解:例题讲解解:从而练 习:例题讲解方法:作差比较法练习:P74 第3题 例2. 如果 16 < x <32 , 4 < y < 8 ,分别求 x + y , 2x – 3y , xy2 , 的取值范围.解: 由16 =x2(x-1)+(x-1)
=(x-1)(x2+1),∵ x2+1>0,
∴ 当x>1时,x3>x2-x+1; 当x=1时,x3=x2-x+1,当x<1时,x3
1,现实世界中,不等关系是普遍存在的。 2,如何用不等式(组)表示不等关系?
3,怎样比较两个实数的大小? 我们用数学符号“≠”,“>”,“<”,“≥”,“≤”连接两个数或代数式,以表示它们之间的不等关系。含有这些不等号的式子叫做不等式. > ,<是严格不等式;≥,≤是非严格不等式.思考:1、右图是限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h ,写成不等式是:_________402、某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%,用不等式可以表示为:( )v≤40A. f ≥ 2.5%或p ≥ 2.3%B. f ≥ 2.5%且p ≥ 2.3%B自学成果展示:3、中国“神舟七号”宇宙飞船飞天取得了最圆满的成功.我们知道,它的飞行速度( )不小于第一宇宙速度( 记作 ),且小于第二宇宙速度(记作 ).><≥≤≤≥≤≥问题1. 设点A与平面 的距离为d,B为平面
上的任意一点,则ABBBdod≤|AB|.二、用不等式(组)来表示不等关系问题2、某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?思考(1 )销售量减少了多少?
(2)现在销售量是多少?(3)销售总收入为多少?
二、用不等式(组)来表示不等关系问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍 请思考:(1)找出两种规格的钢管的数量满足的不等关系.
(2)用不等式(组)表示上述不等关系.分析:假设截得500mm的钢管x根,截得600mm的钢管y根。根据题意,应当有什么样的不等关系呢?(3)截得两种钢管的数量都不能为负.(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;(1)截得两种钢管的总长度不能超过4000mm;二、用不等式(组)来表示不等关系上面三个不等关系,是“且”的关系,要同时满足的话,可以用下面的不等式组来表示:考虑到实际问题的意义,还应有x,y∈Nx,y∈N二、用不等式(组)来表示不等关系课堂练习:书本:P74,练习1、2(1).a与b的和是非负数;(2).某公路立交桥对通过车辆的高度h“限高4m”(3).在一个面积为350平方米的矩形地基
上建造一个仓库,四周是绿地.仓库的长L
大于宽W的4倍.写出L与W的关系a+b≥00
比十位数字大2,试用不等式(组)表示上述关系1.分析:设个位数字为 , 十位数字为 ,则自主学习: p73,了解比较实数大小的方法作差变形判断结论因式分解、配方、通分等手段三、不等式基本原理例1.比较x2-x与x-2的大小.解:(x2-x)-(x-2)=x2-2x+2 =(x-1)2+1,因为(x-1)2≥0,
所以(x2-x)-(x-2)>0,因此x2-x>x-2.比较两个数(式)的大小的方法:(1)作差(2)变形(3)判号(4)结论小结:作差法的步骤:(1)作差→(2)变形→(3)定号→(4)结论其中,变形的方法有:配方法;因式分解法;分子有理化等。 例2:比较下面两式的大小:
小结:作差法的步骤:
(1)作差→(2)变形→(3)定号→(4)结论其中,变形的方法有:配方法;因式分解法;分子有理化等。配方配方因式分解比较两个数(式)的大小的方法:若b>a,结论又会怎样呢? 例4.
(1)已知a>0且a≠1,
比较p与q的大小;
(2)设a>0,b>0且a≠b,比较aabb与baab的大小.例5.设m.>n>0,a>0且a≠1,试比较am+a-m与an+a-n的大小.
五、小结:1.不等关系是普遍存在的2.用不等式(组)来表示不等关系3.不等式基本原理
4.作差比较法
(1)作差→(2)变形→(3)定号→(4)结论其中,变形的方法有:配方法;因式分解法;分子有理化等。姚明身高>奥尼尔身高生活中,我们可用不等式来表示一些不等关系横看成岭侧成峰
远近高低各不同行车速度 V≤40km/h解:x3-(x2-x+1)=x3-x2+x-1
=x2(x-1)+(x-1)
=(x-1)(x2+1),∵ x2+1>0,
∴ 当x>1时,x3>x2-x+1; 当x=1时,x3=x2-x+1,当x<1时,x3
设698mm与518mm分别x与y个练习2 、一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料需要的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨。现有库存磷酸盐10吨、硝酸盐66吨,在此基础上进行生产。请用不等式组把此实例中的不等关系表示出来。分析:设分别生产甲.乙两种肥料为x吨,y吨练习3、某年夏天,我国遭受特大洪灾,灾区学生小李家中经济发生困难,为帮助小李解决开学费用问题,小李所在班级学生(小李除外)决定承担这笔费用。若每人承担12元人民币,则多余84元;若每人承担10元,则不够;若每人承担11元,又多出40元以上。问该班共有多少人?这笔开学费用共多少元?分析:设该班除小李外共有x人,这笔开学费用共y元,则:变式:如果设杂志的单价提高了0.1n元(n∈N*),如何用不等式表示销售的总收入仍不低于20万元呢?你能计算出n在哪个范围内变化吗?分析:销售量减少了0.2n万本,单价为
(2.5+0.1n)元,则可得到销售的总以收入为不低于20万元的不等式可表示为:
(2.5+0.1n)(8-0.2n)≥20二、用不等式(组)来表示不等关系A 例题讲解 例1 某用户计划购买单价分别为60元、70元的单片软件和盒装磁盘,使用资金不超过500元,根据需要,软件至少买3片,磁盘至少买2盒,用不等式组表示软件数x与磁盘数y应满足的条件. 例2 比较下列三组代数式的大小: (1)x2+3与3x; (2) x6+1与x4+x2;(3)例题讲解解:例题讲解解:从而练 习:例题讲解方法:作差比较法练习:P74 第3题 例2. 如果 16 < x <32 , 4 < y < 8 ,分别求 x + y , 2x – 3y , xy2 , 的取值范围.解: 由16
=(x-1)(x2+1),∵ x2+1>0,
∴ 当x>1时,x3>x2-x+1; 当x=1时,x3=x2-x+1,当x<1时,x3
