19.3课题学习 选择方案 课件(共39张PPT)
文档属性
| 名称 | 19.3课题学习 选择方案 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 06:03:39 | ||
图片预览





文档简介
(共39张PPT)
19.3 课题学习 选择方案
人教版八年级下册
知识回顾
1.回顾一次函数的性质和一次函数与方程、不等式之间的关系.
2.一次函数y=5x+435,当x=1时,y=_____,当x=14时,y=______,y随x的增大而________.
3.y1=-x+2,y2=3x-4,当x=______时,y1=y2; 当x_________时,y1>y2;当x________时,y1<y2.
440
505
增大
教学目标
1.会建立实际问题的数学模型,将实际问题转化为数学问题.
2.会综合运用一次函数的图象和性质、方程(组)和不等式(组)等知识解决方案设计问题.
新知导入
思考: 如图, 两射线a和b分别表示甲乙两人跑步路程和时间的关系, 由图象可知, 当t=__________时, 甲跑步的路程等于乙跑步的路程;
当t _________ 时, 甲跑步的路程大于乙跑步的路程.
A
A
>8
8
新知探究
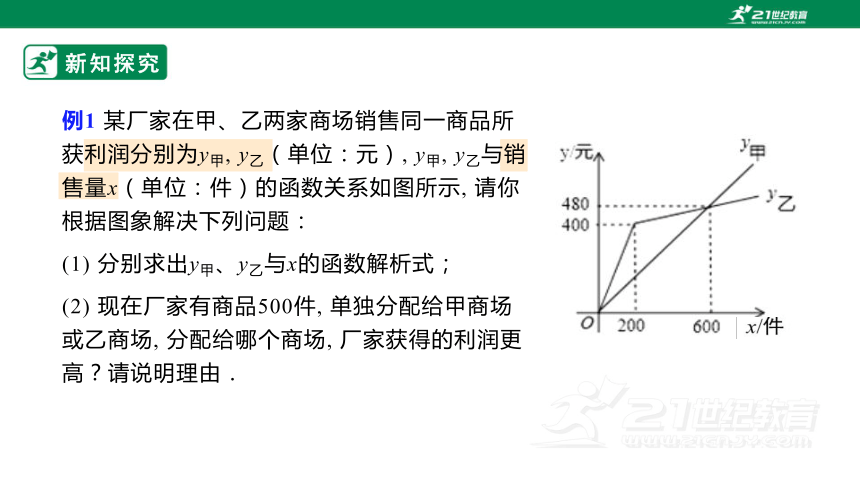
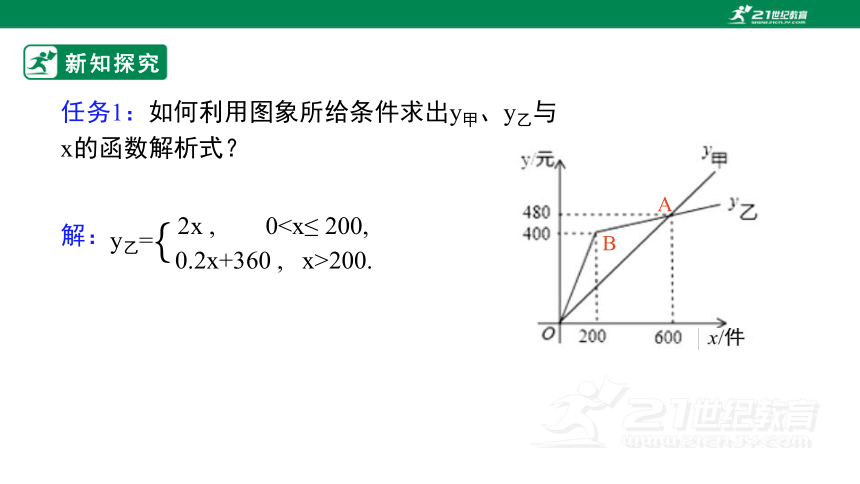
例1 某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲, y乙(单位:元), y甲, y乙与销售量x(单位:件)的函数关系如图所示, 请你根据图象解决下列问题:
(1) 分别求出y甲、y乙与x的函数解析式;
(2) 现在厂家有商品500件, 单独分配给甲商场或乙商场, 分配给哪个商场, 厂家获得的利润更高?请说明理由.
新知探究
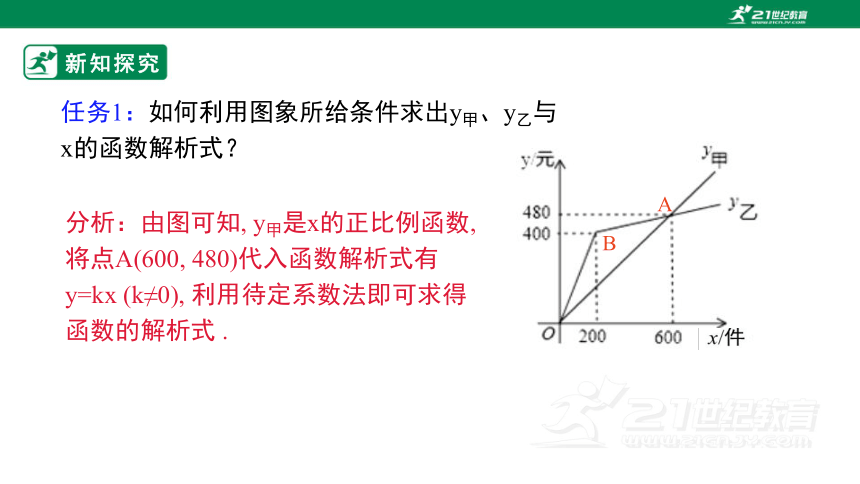
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
分析:由图可知, y甲是x的正比例函数, 将点A(600, 480)代入函数解析式有y=kx (k≠0), 利用待定系数法即可求得函数的解析式 .
新知探究
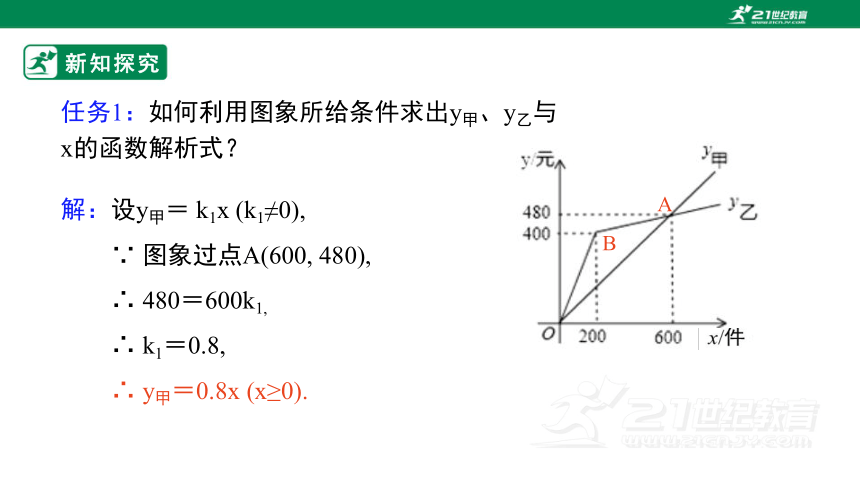
解:设y甲= k1x (k1≠0),
∵ 图象过点A(600, 480),
∴ 480=600k1,
∴ k1=0.8,
∴ y甲=0.8x (x≥0).
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
新知探究
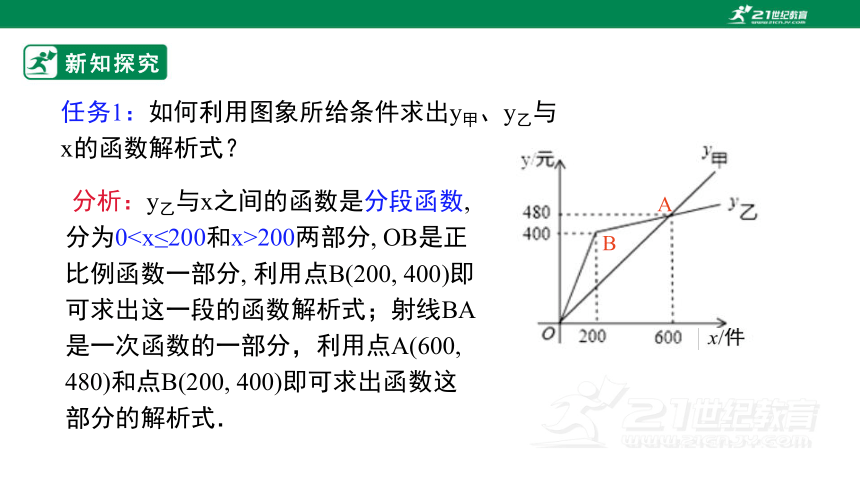
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
分析:y乙与x之间的函数是分段函数, 分为0200两部分, OB是正比例函数一部分, 利用点B(200, 400)即可求出这一段的函数解析式;射线BA是一次函数的一部分,利用点A(600, 480)和点B(200, 400)即可求出函数这部分的解析式.
新知探究
2x , 00.2x+360 , x>200.
y乙=
{
解:
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
新知探究
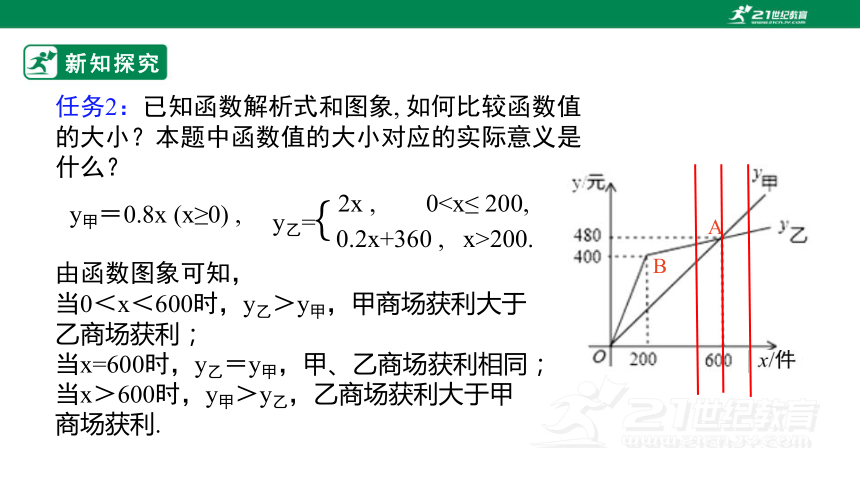
任务2:已知函数解析式和图象, 如何比较函数值的大小?本题中函数值的大小对应的实际意义是什么?
y甲=0.8x (x≥0) ,
2x , 00.2x+360 , x>200.
y乙=
{
A
B
由函数图象可知,
当0<x<600时,y乙>y甲,甲商场获利大于乙商场获利;
当x=600时,y乙=y甲,甲、乙商场获利相同;
当x>600时,y甲>y乙,乙商场获利大于甲商场获利.
新知探究
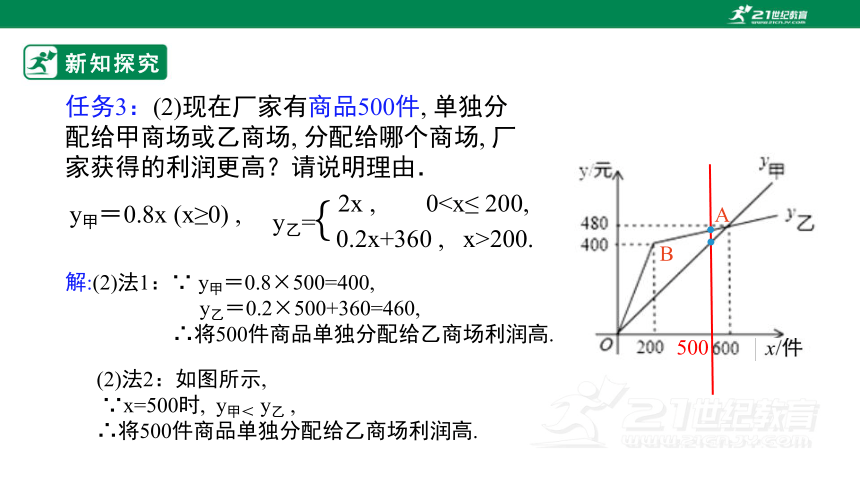
解:(2)法1:∵ y甲=0.8×500=400,
y乙=0.2×500+360=460,
∴将500件商品单独分配给乙商场利润高.
任务3:(2)现在厂家有商品500件, 单独分配给甲商场或乙商场, 分配给哪个商场, 厂家获得的利润更高?请说明理由.
A
B
y甲=0.8x (x≥0) ,
2x , 00.2x+360 , x>200.
y乙=
{
(2)法2:如图所示,
∵x=500时, y甲< y乙 ,
∴将500件商品单独分配给乙商场利润高.
500
新知探究
例2 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表中给出A、B、C三种上宽带网的收费方式.
选择哪种方式能节省上网费用?
新知探究
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
任务1:以收费方式A为例,上网费用是由哪几部分构成的?影响网费变化的因素是什么?
方式A的网费是由月使用费和超时费两部分构成, 影响网费变化的因素是时间 .
新知探究
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
例2
任务2:设上网时间为t小时, 所需费用为y, 你能表示出方式A的上网费用吗?
答:当0≤ t ≤25时, y=30;
当t>25时, y=30+0.05×60(t-25), 即y=3t-45;
30, 0≤ t ≤25 ,
3t-45, t>25 .
=
{
任务3:类比方式A, 你能用数学关系式表示出方式B中上网费用y与上网时间t的关系吗?方式C呢?
新知探究
从表中可以看出:当 0≤x≤50 时, y1=50.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
B 50 50 0.05
当 x>50 时, y2=50+0.0560(x-50)=3x-100.
50 (0≤x≤50)
3x-100 (x>50)
B 方式的函数解析式为: y2=
新知探究
从表中可以看出:无论上网时间多久,每月只用交一次费用即可.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
C 120 不限时
C 方式的函数解析式为: y3= 120 (x≥0)
= 时, 3t-45=50, 解方程,;
= 时, 3t-100=120, 解方程, 得 ;
= 时, 3t-45=120, 解方程, 得 t=55.
新知探究
任务4:你能在同一坐标系下画出三个函数解析式的图象吗?
任务5:如何求交点坐标?图象交点有什么实际意义?
=120 .
30, 0≤ t ≤25,
3t-45, t>25 .
=
{
=
50, 0≤ t≤50,
3t-100, t>50 .
{
55
新知探究
当时, yA最小 ,
当时, yC最小 ,
当时, yB最小 ,
任务6:如何判断函数值yA、yB、yC哪个最小呢?
55
新知探究
任务7:通过上述比较,函数值最小的实际意义是什么?
55
当时, yA最小 ,
当时, yC最小 ,
当时, yB最小 ,
选择方式A最省钱;
选择方式B最省钱;
选择方式C最省钱;
新知探究
例2 怎样选取上网收费方式?
55
当时, yA最小 ,
当时, yC最小 ,
当时, yB最小 ,
选择方式A最省钱;
选择方式B最省钱;
选择方式C最省钱;
解:
新知探究
用一次函数选择最佳方案的一般步骤
1.析:分析题意,弄清数量关系.
2.列:列出函数解析式、不等式或方程.
3.求:求出自变量取不同值对应的函数值的大小,或函数的最大(小)值.
4.选:结合实际需要选择最佳方案.
新知练习
甲种客车 乙种客车
载客量(人/辆) 45 30
租金(元/辆) 400 280
某学校计划在总费用 2300 元的限额内,租用汽车送 234 名学生和 6 名教师集体外出活动,每辆汽车上至少要有 1 名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
问题2 怎样租车?
新知练习
思考1 租车方案有哪几种?
①单独租用甲种客车;②单独租用乙种客车;
③同时租用甲种客车和乙种客车.
思考2 如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于 6 辆,不能超过 8 辆.
新知练习
设租用甲种客车 x 辆,则租用乙种客车 (6-x) 辆.
租车总费用为 y 元.
从人数上:6 名教师和 234 名学生共计 240 人,所以甲种客车和乙种客车总共的载客量要≥240.
从费用上:学校计划的费用是 2300 元,所以甲种客车和乙种客车总共的费用要≤2300.
新知练习
45x+30(6-x)≥240
400x+280(6-x)≤2300
由题意可得:
解得:4≤ x ≤ 5
结合实际意义,有几种选择?哪种选择更省钱?
新知练习
由题意可得: y=400x+280(6-x)
=120x+1680(4≤x≤5)
虽然 4≤ x≤ 5,但是根据实际意义,x只能取4或5.
设租用甲种客车 x 辆,则租用乙种客车 (6-x) 辆.
租车总费用为 y 元.
新知练习
方案一:当 x=4 时,即需用甲种客车 4 辆,乙种客车 2 辆.
此时 y=1204+1680=2160元.
方案二:当 x=5 时,即需用甲种客车 5 辆,乙种客车 1 辆.
此时 y=1205+1680=2280元.
由上述可知:选择方案一更划算.你能不计算就得出结论吗?
新知练习
通过一次函数的性质来判断:
费用 y=120x+1680(4≤x≤5),可以看出函数值 y 随着自变量 x 的增大而增大,因为 5>4,所以当 x=4 时,所花费的费用更少.
选择最佳方案实际上是在比较的基础上完成的,在没有学习函数之前,一般是将全部方案一一列举出来,然后根据题意选择一个最佳方案;学习函数之后,我们可以利用函数的性质,直接求出最佳方案.
新知练习
问题2 一家电信公司提供两种手机月通话方式供用户选择,其中一种有月租,另一种无月租,这两种收费方式的通话费用 y(元)与通话时间 x(分钟)之间的函数关系如图所示.请你判断下列叙述是否正确.
y
x
l2
400
O
20
400
l1
新知练习
(1)l1描述的是无月租费用的收费方式.
(2)l2描述的是有月租费用的收费方式.
(3)当每月的通话时间超过 400 分钟的时候选择有月租的收费方式更省钱.
错
正确,超过 400 分钟后, l1 方式的费用小于 l2 方式的费用.
错
y
x
l2
400
O
20
400
l1
课堂总结
1.析:分析题意,弄清数量关系.
2.列:列出函数解析式、不等式或方程.
3.求:求出自变量取不同值对应的函数值的大小,或函数的最大(小)值.
4.选:结合实际需要选择最佳方案.
用一次函数选择最佳方案的步骤是什么?
课堂练习
C
课堂练习
D
课堂练习
x=20
0<x<20
课堂练习
4. 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲、乙两厂的印刷费用 y(千元)与证书数量x(千个)的函数关系图象分别如图所示,下列说法:①甲厂的制版费为1千元;②当印制证书4千个时,选择乙厂印刷节省费用;③当印制证书8千个时,选择乙厂印刷节省费用.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
C
新知练习
5. 广安某水果店计划购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) 售价(元/千克)
甲种 5 8
乙种 9 13
(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?
(2)若该水果店决定乙种水果的进货量不超过甲种水果进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?此时利润为多少元?
课堂练习
【思路分析】(1)根据计划购进甲、乙两种新出产的水果共140千克,进而利用该水果店预计进货款为1000元,得出等式求出即可;(2)利用两种水果每千克的利润表示出总利润,再利用一次函数的增减性得出最大值即可.
解:(1)设购进甲种水果x千克,则购进乙种水果(140-x)千克.根据题意,得5x+9(140-x)=1000,解得x=65,∴140-x=75.答:购进甲种水果65千克,乙种水果75千克;
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
19.3 课题学习 选择方案
人教版八年级下册
知识回顾
1.回顾一次函数的性质和一次函数与方程、不等式之间的关系.
2.一次函数y=5x+435,当x=1时,y=_____,当x=14时,y=______,y随x的增大而________.
3.y1=-x+2,y2=3x-4,当x=______时,y1=y2; 当x_________时,y1>y2;当x________时,y1<y2.
440
505
增大
教学目标
1.会建立实际问题的数学模型,将实际问题转化为数学问题.
2.会综合运用一次函数的图象和性质、方程(组)和不等式(组)等知识解决方案设计问题.
新知导入
思考: 如图, 两射线a和b分别表示甲乙两人跑步路程和时间的关系, 由图象可知, 当t=__________时, 甲跑步的路程等于乙跑步的路程;
当t _________ 时, 甲跑步的路程大于乙跑步的路程.
A
A
>8
8
新知探究
例1 某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲, y乙(单位:元), y甲, y乙与销售量x(单位:件)的函数关系如图所示, 请你根据图象解决下列问题:
(1) 分别求出y甲、y乙与x的函数解析式;
(2) 现在厂家有商品500件, 单独分配给甲商场或乙商场, 分配给哪个商场, 厂家获得的利润更高?请说明理由.
新知探究
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
分析:由图可知, y甲是x的正比例函数, 将点A(600, 480)代入函数解析式有y=kx (k≠0), 利用待定系数法即可求得函数的解析式 .
新知探究
解:设y甲= k1x (k1≠0),
∵ 图象过点A(600, 480),
∴ 480=600k1,
∴ k1=0.8,
∴ y甲=0.8x (x≥0).
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
新知探究
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
分析:y乙与x之间的函数是分段函数, 分为0
新知探究
2x , 0
y乙=
{
解:
任务1:如何利用图象所给条件求出y甲、y乙与x的函数解析式?
A
B
新知探究
任务2:已知函数解析式和图象, 如何比较函数值的大小?本题中函数值的大小对应的实际意义是什么?
y甲=0.8x (x≥0) ,
2x , 0
y乙=
{
A
B
由函数图象可知,
当0<x<600时,y乙>y甲,甲商场获利大于乙商场获利;
当x=600时,y乙=y甲,甲、乙商场获利相同;
当x>600时,y甲>y乙,乙商场获利大于甲商场获利.
新知探究
解:(2)法1:∵ y甲=0.8×500=400,
y乙=0.2×500+360=460,
∴将500件商品单独分配给乙商场利润高.
任务3:(2)现在厂家有商品500件, 单独分配给甲商场或乙商场, 分配给哪个商场, 厂家获得的利润更高?请说明理由.
A
B
y甲=0.8x (x≥0) ,
2x , 0
y乙=
{
(2)法2:如图所示,
∵x=500时, y甲< y乙 ,
∴将500件商品单独分配给乙商场利润高.
500
新知探究
例2 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表中给出A、B、C三种上宽带网的收费方式.
选择哪种方式能节省上网费用?
新知探究
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
任务1:以收费方式A为例,上网费用是由哪几部分构成的?影响网费变化的因素是什么?
方式A的网费是由月使用费和超时费两部分构成, 影响网费变化的因素是时间 .
新知探究
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
例2
任务2:设上网时间为t小时, 所需费用为y, 你能表示出方式A的上网费用吗?
答:当0≤ t ≤25时, y=30;
当t>25时, y=30+0.05×60(t-25), 即y=3t-45;
30, 0≤ t ≤25 ,
3t-45, t>25 .
=
{
任务3:类比方式A, 你能用数学关系式表示出方式B中上网费用y与上网时间t的关系吗?方式C呢?
新知探究
从表中可以看出:当 0≤x≤50 时, y1=50.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
B 50 50 0.05
当 x>50 时, y2=50+0.0560(x-50)=3x-100.
50 (0≤x≤50)
3x-100 (x>50)
B 方式的函数解析式为: y2=
新知探究
从表中可以看出:无论上网时间多久,每月只用交一次费用即可.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
C 120 不限时
C 方式的函数解析式为: y3= 120 (x≥0)
= 时, 3t-45=50, 解方程,;
= 时, 3t-100=120, 解方程, 得 ;
= 时, 3t-45=120, 解方程, 得 t=55.
新知探究
任务4:你能在同一坐标系下画出三个函数解析式的图象吗?
任务5:如何求交点坐标?图象交点有什么实际意义?
=120 .
30, 0≤ t ≤25,
3t-45, t>25 .
=
{
=
50, 0≤ t≤50,
3t-100, t>50 .
{
55
新知探究
当时, yA最小 ,
当时, yC最小 ,
当时, yB最小 ,
任务6:如何判断函数值yA、yB、yC哪个最小呢?
55
新知探究
任务7:通过上述比较,函数值最小的实际意义是什么?
55
当时, yA最小 ,
当时, yC最小 ,
当时, yB最小 ,
选择方式A最省钱;
选择方式B最省钱;
选择方式C最省钱;
新知探究
例2 怎样选取上网收费方式?
55
当时, yA最小 ,
当时, yC最小 ,
当时, yB最小 ,
选择方式A最省钱;
选择方式B最省钱;
选择方式C最省钱;
解:
新知探究
用一次函数选择最佳方案的一般步骤
1.析:分析题意,弄清数量关系.
2.列:列出函数解析式、不等式或方程.
3.求:求出自变量取不同值对应的函数值的大小,或函数的最大(小)值.
4.选:结合实际需要选择最佳方案.
新知练习
甲种客车 乙种客车
载客量(人/辆) 45 30
租金(元/辆) 400 280
某学校计划在总费用 2300 元的限额内,租用汽车送 234 名学生和 6 名教师集体外出活动,每辆汽车上至少要有 1 名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
问题2 怎样租车?
新知练习
思考1 租车方案有哪几种?
①单独租用甲种客车;②单独租用乙种客车;
③同时租用甲种客车和乙种客车.
思考2 如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于 6 辆,不能超过 8 辆.
新知练习
设租用甲种客车 x 辆,则租用乙种客车 (6-x) 辆.
租车总费用为 y 元.
从人数上:6 名教师和 234 名学生共计 240 人,所以甲种客车和乙种客车总共的载客量要≥240.
从费用上:学校计划的费用是 2300 元,所以甲种客车和乙种客车总共的费用要≤2300.
新知练习
45x+30(6-x)≥240
400x+280(6-x)≤2300
由题意可得:
解得:4≤ x ≤ 5
结合实际意义,有几种选择?哪种选择更省钱?
新知练习
由题意可得: y=400x+280(6-x)
=120x+1680(4≤x≤5)
虽然 4≤ x≤ 5,但是根据实际意义,x只能取4或5.
设租用甲种客车 x 辆,则租用乙种客车 (6-x) 辆.
租车总费用为 y 元.
新知练习
方案一:当 x=4 时,即需用甲种客车 4 辆,乙种客车 2 辆.
此时 y=1204+1680=2160元.
方案二:当 x=5 时,即需用甲种客车 5 辆,乙种客车 1 辆.
此时 y=1205+1680=2280元.
由上述可知:选择方案一更划算.你能不计算就得出结论吗?
新知练习
通过一次函数的性质来判断:
费用 y=120x+1680(4≤x≤5),可以看出函数值 y 随着自变量 x 的增大而增大,因为 5>4,所以当 x=4 时,所花费的费用更少.
选择最佳方案实际上是在比较的基础上完成的,在没有学习函数之前,一般是将全部方案一一列举出来,然后根据题意选择一个最佳方案;学习函数之后,我们可以利用函数的性质,直接求出最佳方案.
新知练习
问题2 一家电信公司提供两种手机月通话方式供用户选择,其中一种有月租,另一种无月租,这两种收费方式的通话费用 y(元)与通话时间 x(分钟)之间的函数关系如图所示.请你判断下列叙述是否正确.
y
x
l2
400
O
20
400
l1
新知练习
(1)l1描述的是无月租费用的收费方式.
(2)l2描述的是有月租费用的收费方式.
(3)当每月的通话时间超过 400 分钟的时候选择有月租的收费方式更省钱.
错
正确,超过 400 分钟后, l1 方式的费用小于 l2 方式的费用.
错
y
x
l2
400
O
20
400
l1
课堂总结
1.析:分析题意,弄清数量关系.
2.列:列出函数解析式、不等式或方程.
3.求:求出自变量取不同值对应的函数值的大小,或函数的最大(小)值.
4.选:结合实际需要选择最佳方案.
用一次函数选择最佳方案的步骤是什么?
课堂练习
C
课堂练习
D
课堂练习
x=20
0<x<20
课堂练习
4. 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲、乙两厂的印刷费用 y(千元)与证书数量x(千个)的函数关系图象分别如图所示,下列说法:①甲厂的制版费为1千元;②当印制证书4千个时,选择乙厂印刷节省费用;③当印制证书8千个时,选择乙厂印刷节省费用.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
C
新知练习
5. 广安某水果店计划购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) 售价(元/千克)
甲种 5 8
乙种 9 13
(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?
(2)若该水果店决定乙种水果的进货量不超过甲种水果进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?此时利润为多少元?
课堂练习
【思路分析】(1)根据计划购进甲、乙两种新出产的水果共140千克,进而利用该水果店预计进货款为1000元,得出等式求出即可;(2)利用两种水果每千克的利润表示出总利润,再利用一次函数的增减性得出最大值即可.
解:(1)设购进甲种水果x千克,则购进乙种水果(140-x)千克.根据题意,得5x+9(140-x)=1000,解得x=65,∴140-x=75.答:购进甲种水果65千克,乙种水果75千克;
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
