探索三角形全等的条件

课件54张PPT。探索三角形全等的条件知识回顾能够完全重合的两个图形叫做全等图形.全等图形:知识回顾1、 什么叫全等三角形？能够完全重合的两个三角形叫 全等三角形。2、全等三角形的性质全等三角形的对应边相等，
全等三角形的对应角相等。两个三角形完全重合时，
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
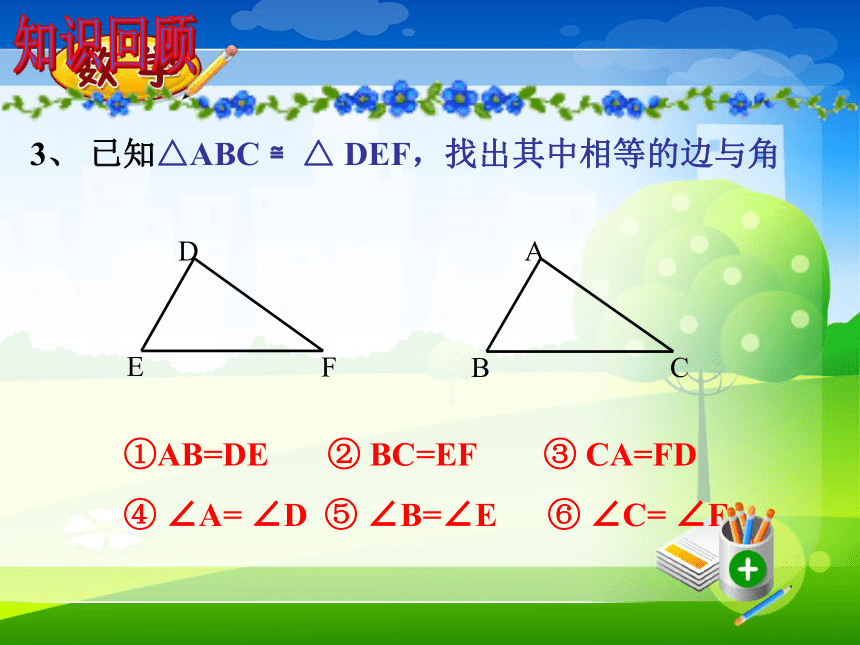
互相重合的角叫对应角.知识回顾3、 已知△ABC ≌△ DEF，找出其中相等的边与角①AB=DE ② BC=EF ③ CA=FD
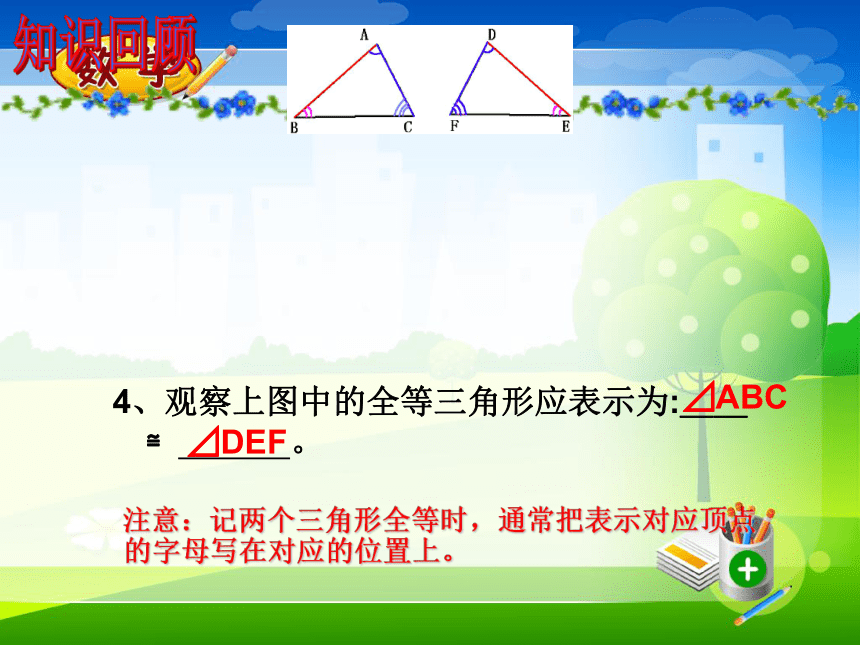
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F知识回顾4、观察上图中的全等三角形应表示为:＿＿ ≌ 。
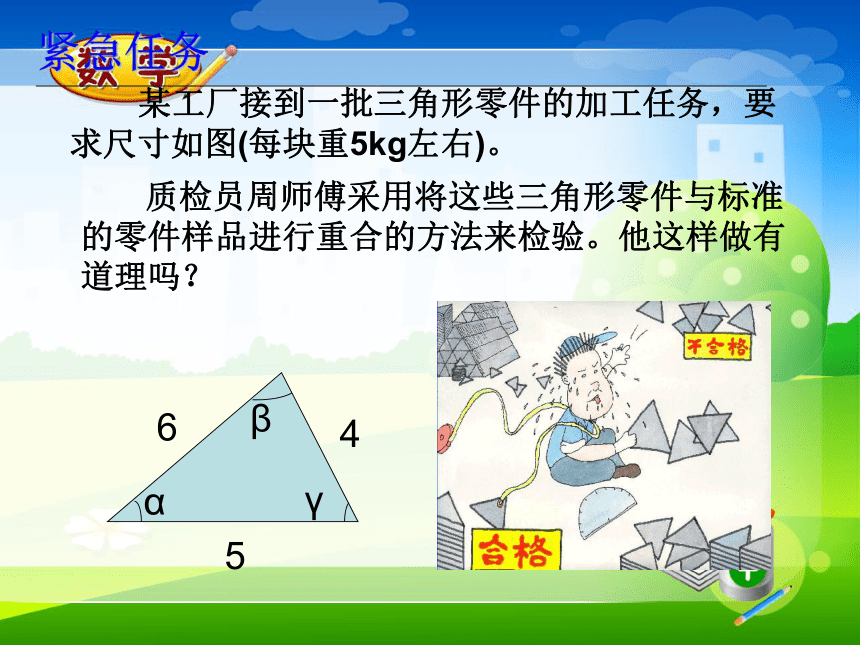
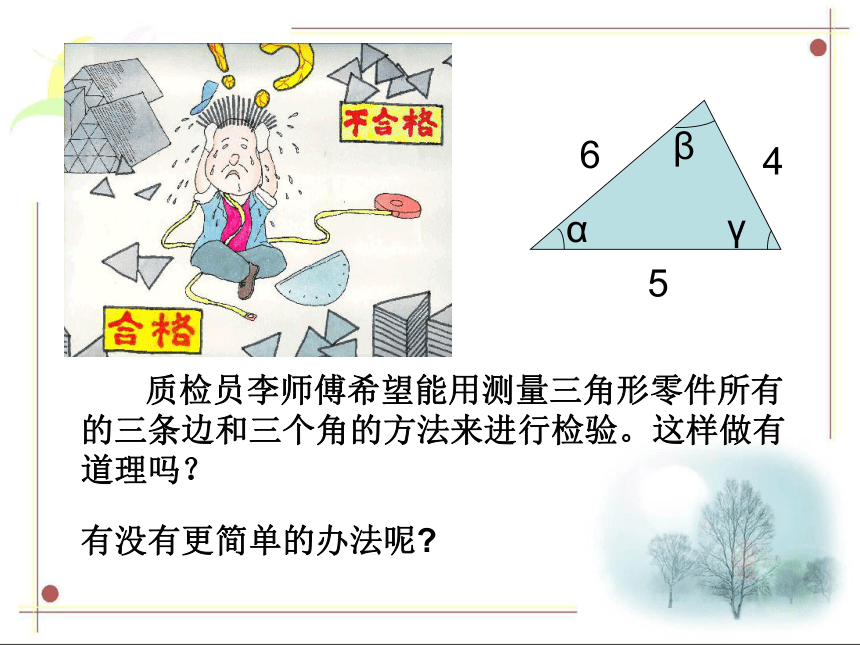
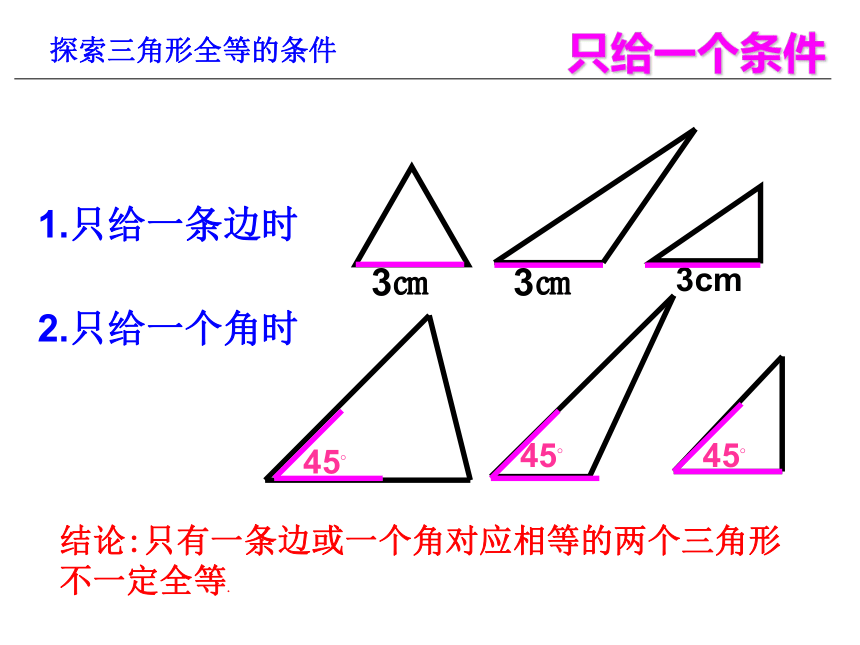
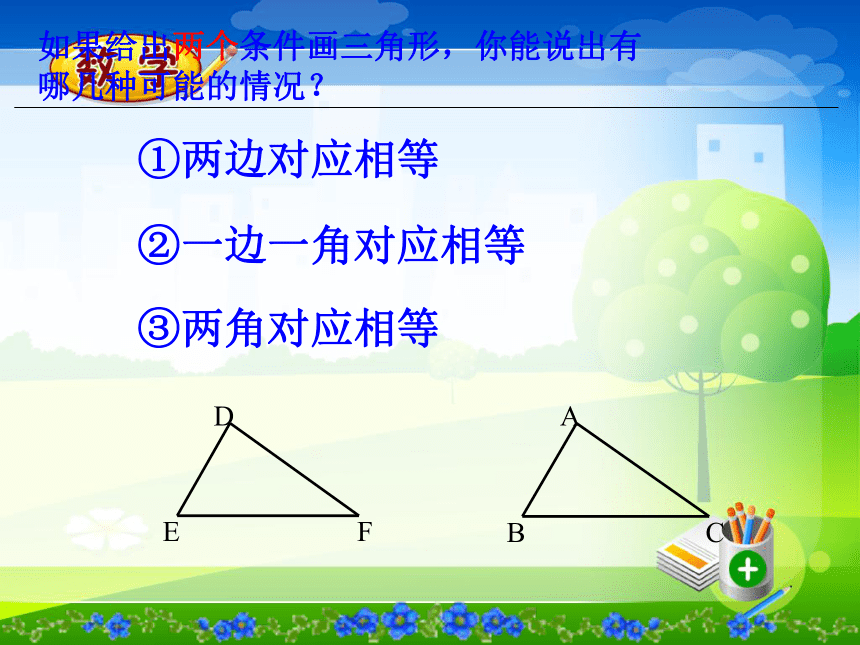
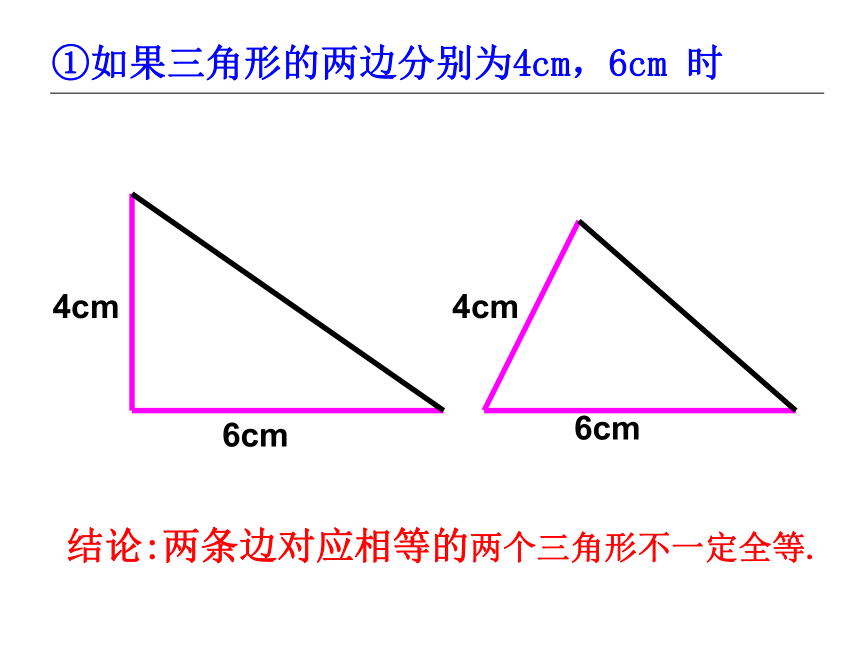
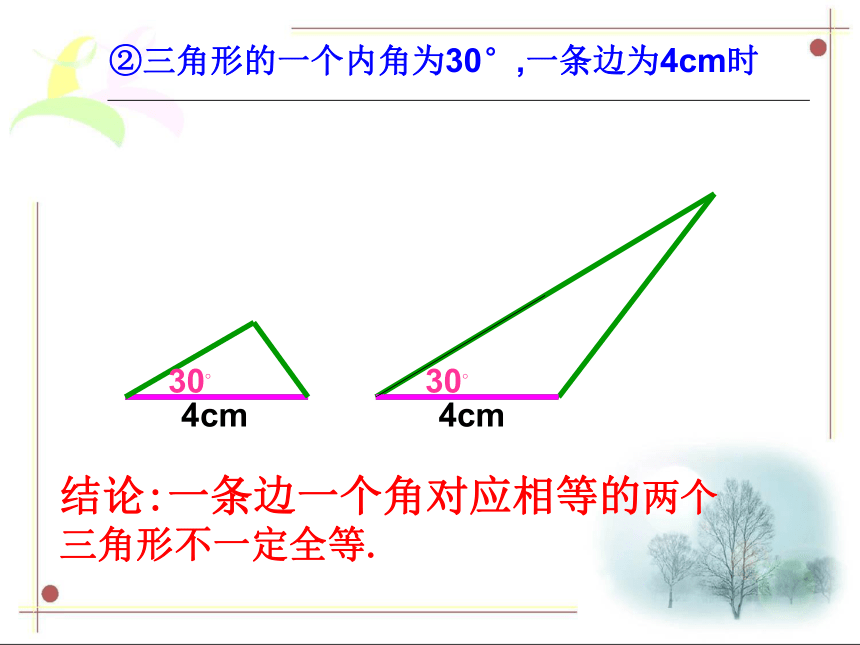
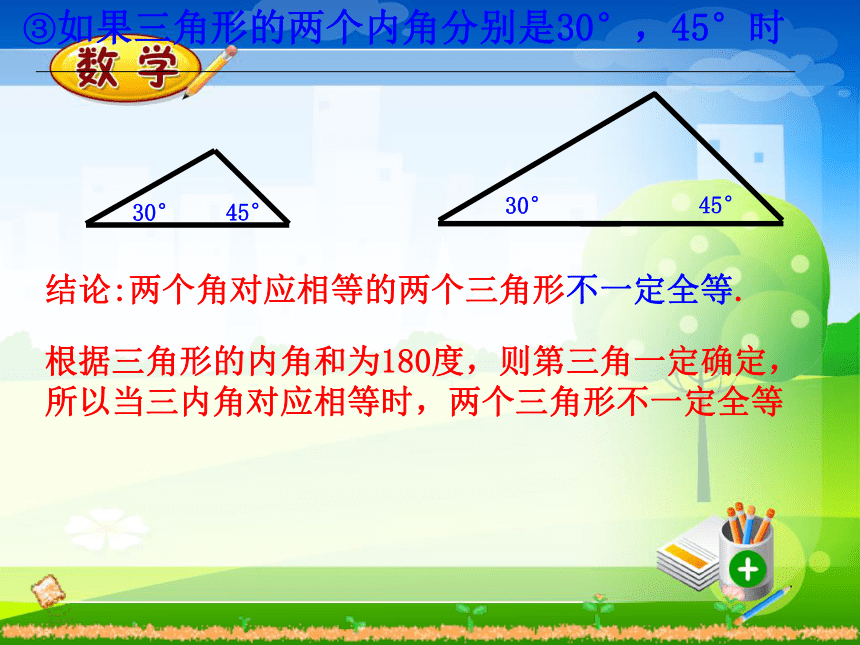
⊿ABC⊿DEF注意：记两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上。　　　某工厂接到一批三角形零件的加工任务，要求尺寸如图(每块重5kg左右)。紧急任务 质检员周师傅采用将这些三角形零件与标准的零件样品进行重合的方法来检验。他这样做有道理吗？有没有更简单的办法呢? 质检员李师傅希望能用测量三角形零件所有的三条边和三个角的方法来进行检验。这样做有道理吗？探索三角形全等的条件1.只给一条边时只给一个条件2.只给一个角时结论:只有一条边或一个角对应相等的两个三角形不一定全等.①两边对应相等③两角对应相等②一边一角对应相等如果给出两个条件画三角形，你能说出有哪几种可能的情况？①如果三角形的两边分别为4cm，6cm 时结论:两条边对应相等的两个三角形不一定全等.结论:一条边一个角对应相等的两个三角形不一定全等.②三角形的一个内角为30°,一条边为4cm时结论:两个角对应相等的两个三角形不一定全等.根据三角形的内角和为180度，则第三角一定确定，所以当三内角对应相等时，两个三角形不一定全等③如果三角形的两个内角分别是30°，45°时 如果两个三角形有三个条件（边或角）分别对应相等，那么有哪几种可能的情况？答：1、一边两角（1）两角夹边 ASA
（2）两角不夹边 AAS
2、两边一角（1）两边夹角 SAS
（2）两边不夹角 SSA
3、三边 SSS
4、三角 AAA AAA不成立。ASA与AAS等价。是不是六种情况都能得到全等三角形呢?SSSSASASA分组探究每组选择两个方案进行探究。并完成口头探究报告。（成立）（成立）（成立）（不成立）你能想到哪些方法来检验三角形零件是否合格？SSS ASA AAS SAS哪种方法用到的工具最少？请找出下图中的全等三角形AB=DE（已知）BC=EF （已知）AC=DF （已知）（SSS）用SSS公理证明的标准书写格式：在△ABC和△DEF中①准备条件：证全等要用的间接条件要先证好②三角形全等书写三步骤：写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤：写在大括号里的三个条件只能是“已知、已证、公共边、公共角、对顶角相等”五种之一　A　C　B　D证明：∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC（已知）BD=CD（已证）AD=AD（公共边）∴△ABD≌△ACD（SSS）例1 如图, △ABC是一个钢架，AB=AC,AD是连接A与BC中点D的支架，求证： △ABD≌△ACD若要求证：∠B=∠C，你会吗？探索与思考例2 小明有一块“飞镖”，想知道∠B和∠C是否相等，他没有量角器，只有刻度尺。经过小明测量，AC=AB，DC=DB，你能告诉小明∠B和∠C是否相等吗？CABD证明：连接AD在△ABD与△ACD中AB=AC（已知）BD=CD（已证）AD=AD（公共边）∴△ABD≌△ACD（SSS）∴ ∠B和∠C （全等三角形的对应角相等）生活中的三角形 鸭绿江大桥上的三角形结构输电铁塔上的三角形结构
取出课前自制长度适当的木条，把它们分别做成三角形和四边形框架，并拉动它们。你发现什么？三角形的稳定性。 做一做 想一想 三角形的大小和形状是固定不变的，而四边形
的形状会改变。 只要三角形三边的长度确定了，这个三形的形状和大小就确定，三角形的这个性质叫 四边形不具有稳定性，你能想出什么方法
让它们的形状不发生改变吗？ 试一试跳转收获与体会本节课你学到了什么？
发现了什么？
有什么收获？
还存在什么没有解决的问题？ 　　本节课我们应用分类讨论的方法对三角形全等的条件进行了探索，经历了用“画图、剪切、重叠”的方法验证两个三角形全等的过程，探索出能得到两个三角形全等的四种条件 ，并应用SSS公理对三角形全等进行了进一步的学习。
　　我们还知道了三角形具有稳定性，只要三角形的三边长度确定了，这个三角形的形状和大小就确定了。在生活实践中，三角形的稳定性有广泛的应用。
本节课用到的方法同学们要用心体会，今后的学习中我们还会不断地应用这些方法。课堂小结作业课本P140习题5.8 第1、2 题课件制作：姜日东再见本课时学习结束 丹东市第十四中学
姜日东探索三角形全等的条件2边边边公理知识回顾1、 什么叫全等三角形？能够完全重合的两个三角形叫 全等三角形。2、全等三角形的性质全等三角形的对应边相等，
全等三角形的对应角相等。两个三角形完全重合时，
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角. 如果两个三角形有三个条件（边或角）分别对应相等，那么有哪几种可能的情况？ 1、一边两角（1）两角夹边 ASA
（2）两角不夹边 AAS
2、两边一角（1）两边夹角 SAS
（2）两边不夹角 SSA
3、三边 SSS
4、三角 AAA其中哪些情况能够得到全等三角形呢?①准备条件：证全等要用的间接条件要先证好②三角形全等书写三步骤：写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤：写在大括号里的三个条件只能是“已知、已证、公共边、公共角、对顶角相等”五种之一AB=DE（已知）BC=EF （已知）AC=DF （已知）（SSS）用SSS公理证明的标准书写格式：在△ABC和△DEF中例1 已知：如图，AB=AD，BC=CD，
求证：△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC（SSS）证明：在△ABC和△ADC中=已知已知 公共边　A　C　B　D 分析：要证明两个三角形全等，需要那些条件？证明：∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC（已知）BD=CD（已证）AD=AD（公共边）∴△ABD≌△ACD（SSS）例2 如图, △ABC是一个钢架，AB=AC,AD是连接A与BC中点D的支架，求证： △ABD≌△ACD若要求证：∠B=∠C，你会吗？例题3已知: 如图,点B、E、C、F在同一直线上 ,
AB = DE ,AC = DF ,BE = CF .
求证: ∠ A =∠ D
CE证明:∴ △ABC ≌ △DEF ( SSS )∵ BE = CF∴ BC = EF∴ BE+EC = CF+CE练习 1如图已知: A、C、D、F四点在同一直线上，
AB = DE ,BC = EF ,AC = DF。
求证: AB ∥ DE分析:AB ∥ DE ∠ A =∠ D△ABC ≌ △DEF ( SSS )AB = DE BC = EF AC = DF证明:在△ABC 和△DEF中AB = DE
BC = EF
AC = DF∴ △ABC ≌ △DEF ( SSS )∴ AB ∥ DE ∴ ∠ A =∠ D甲(全等三角形对应角相等)(内错角相等两直线平行)如图已知: A、C、D、F四点在同一直线上,
AB = DE ,BC = EF ,AC = DF。
求证: AB ∥ DE练习 1 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 甲练习 2练习2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF乙练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF乙练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习：1、如图，AB＝AC，BD＝CD，BH＝CH，图中有几组全等的三角形？它们全等的条件是什么？HDCBA解：有三组。　　　　　　　　
在△ABH和△ACH中 ∵AB=AC，BH=CH，AH=AH　∴△ABH≌△ACH（SSS）；∵BD=CD，BH=CH，DH=DH
∴△DBH≌△DCH（SSS）　在△ABH和△ACH中
∵AB=AC，BD=CD，AD=AD　∴△ABD≌△ACD（SSS）；在△ABH和△ACH中BCBC△DCBBF=DC或 BD=FCABCD练习2。解： △ABC≌△DCB
理由如下：
AB = CD
AC = BD
=
△ABD ≌ （ ） S S S （1）如图，AB=CD，AC=BD，△ABC和△DCB是否全等？试说明理由。 （2）如图，D、F是线段BC上的两点，
AB=CE，AF=DE，要使△ABF≌△ECD ，
还需要条件
AE B D F C
练习3、如图，在四边形ABCD中，AB=CD,AD=CB,求证：∠ A= ∠ C. 证明：在△ABD和△CDB中DABCAB=CDAD=CBBD=DB∴△ABD≌△ACD（SSS）（已知）（已知）（公共边）∴ ∠ A= ∠ C （全等三角形的对应角相等）你能说明AB∥CD，AD∥BC吗？解：①∵E、F分别是AB，CD的中点（ ）又∵AB=CD∴AE=CF在△ADE与△CBF中AE==∴△ADE≌△CBF ( )∴AE= AB CF= CD（ ）补充练习：如图，已知AB=CD，AD=CB，E、F分别是AB，CD的中点，且DE=BF，说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )=思考 已知AC=FE，BC=DE，点A，D，B，F在一条直线上，AD=FB（如图），要用“边边边”证明△ABC ≌△ FDE，除了已知中的AC=FE，BC=DE以外，还应该有什么条件？怎样才能得到这个条件？解：要证明△ABC ≌△ FDE，还应该有AB=DF这个条件∵ DB是AB与DF的公共部分，且AD=BF
∴ AD+DB=BF+DB
即 AB=DF 已知三角形三条边分别是4cm，5cm，6cm，画出这个三角形1. 画线段AB=6cm，2. 在直尺上用圆规取5cm，然后以A点为圆心，画弧。3. 接着又在直尺上用圆规取4cm，然后以B点为圆心，画弧，交原弧于点C。画法：4. 连接AC，BC，?ABC就是我们要求所画的三角形C6cm5cm4cm返幻灯片 5回 以2.5cm，3.5cm为三角形的两边，长度为2.5cm的边所对的角为40° ，情况又怎样？动手画一画，你发现了什么？D结论：两边及其一边所对的角相等，两个三角形不一定全等回到讨论页面