全等三角形的判定课件
图片预览



文档简介
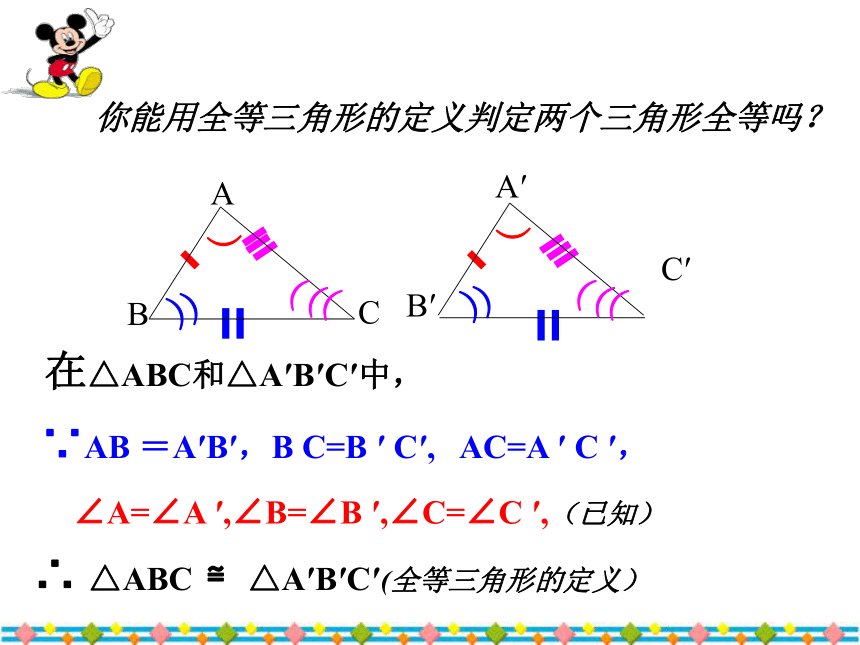
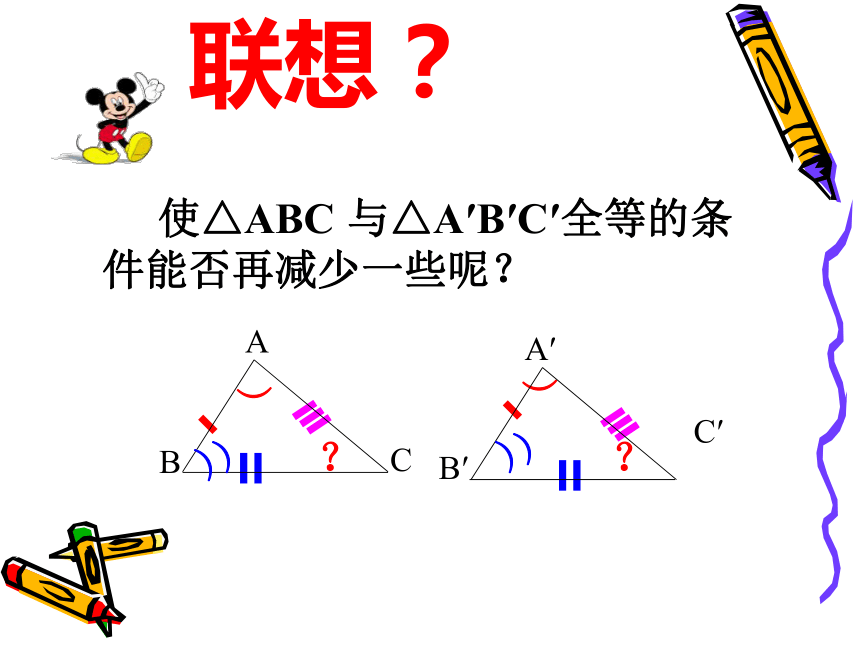
课件44张PPT。知识回顾(1) 什么叫全等三角形?(2)全等三角形有哪些性质?全等三角形的对应边、对应角分别相等。能够完全重合的两个三角形叫做全等三角形。思考:组成三角形的基本元素有几个?三条边和三个内角
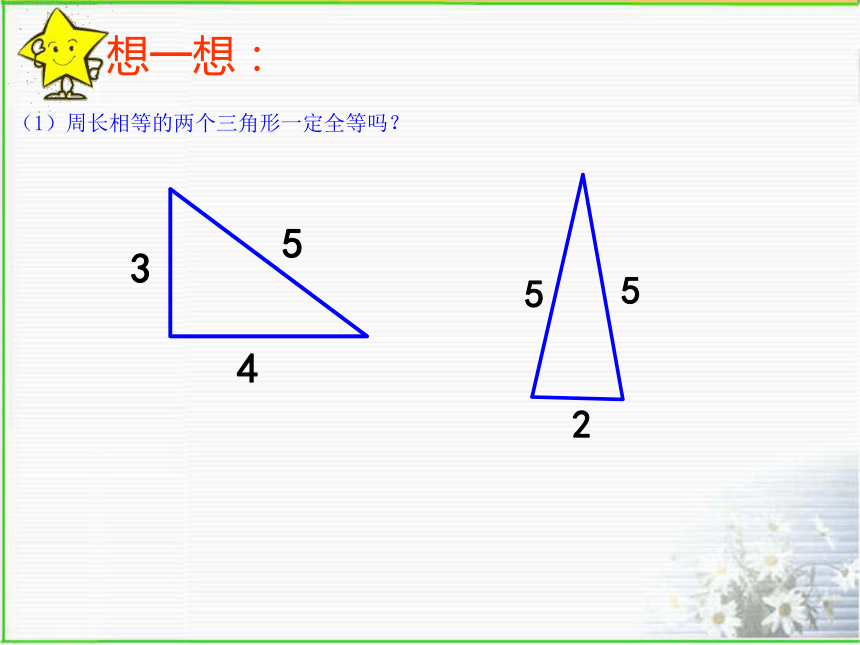
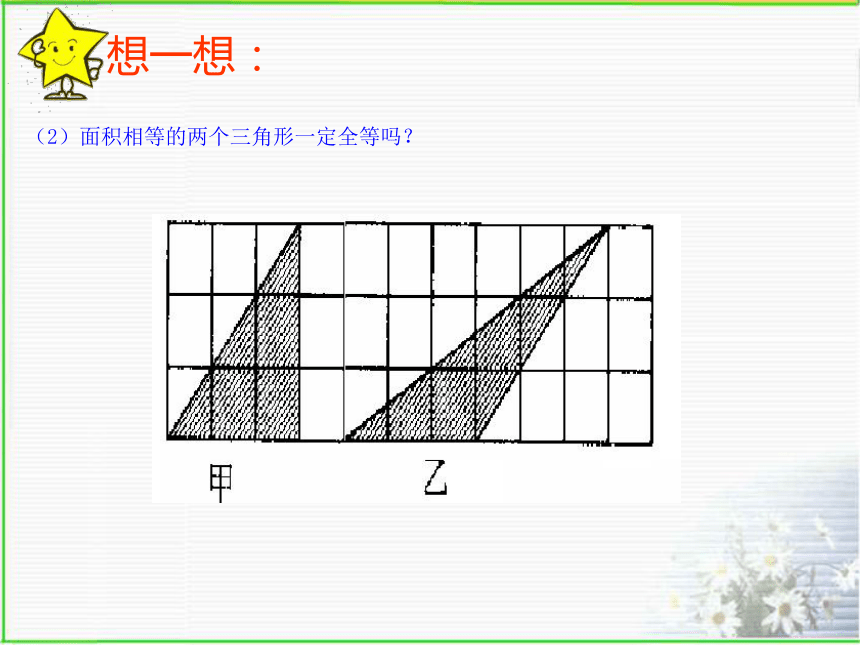
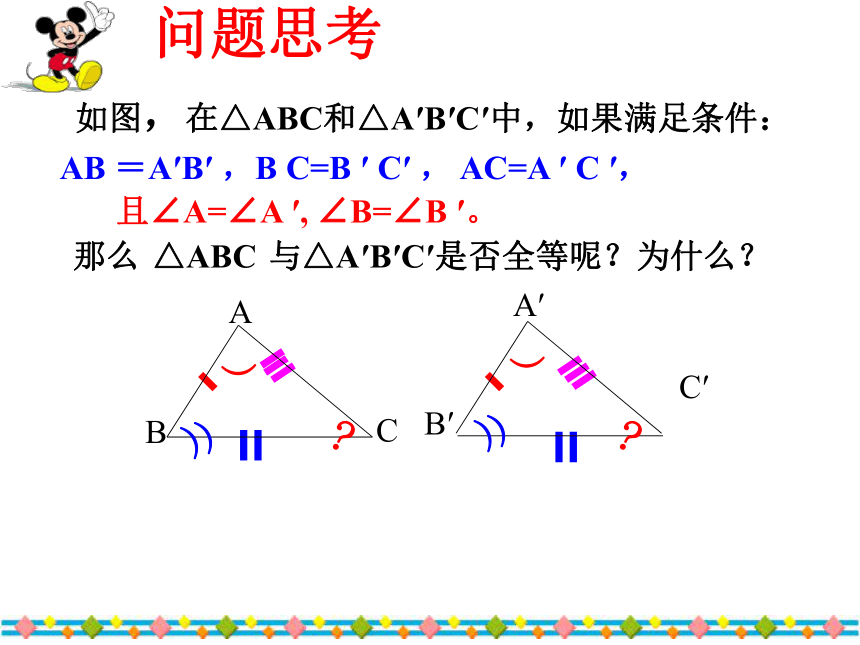
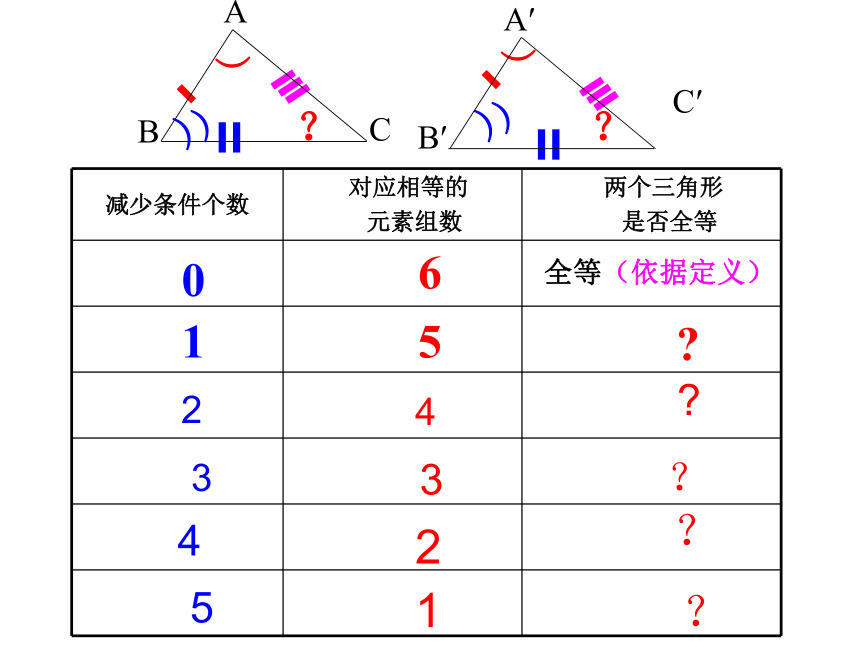
某检查人员到工厂检查三角形模型尺寸是否合格。其中标准模型尺寸如图,如果你是检查人员,你至少需要量出几个数据,才能判断出两个三角形模型全等呢?645βγα帮帮我探索全等三角形的判定条件(1)周长相等的两个三角形一定全等吗?想一想:想一想:(2)面积相等的两个三角形一定全等吗?∵AB =A′B′,B C=B ′ C′, AC=A ′ C ′,∴ △ABC ≌△A′B′C′(全等三角形的定义)∠A=∠A ′,∠B=∠B ′,∠C=∠C ′,(已知)AB =A′B′ ,B C=B ′ C′ , AC=A ′ C ′,且∠A=∠A ′, ∠B=∠B ′。那么 △ABC 与△A′B′C′是否全等呢?为什么?1
5
?
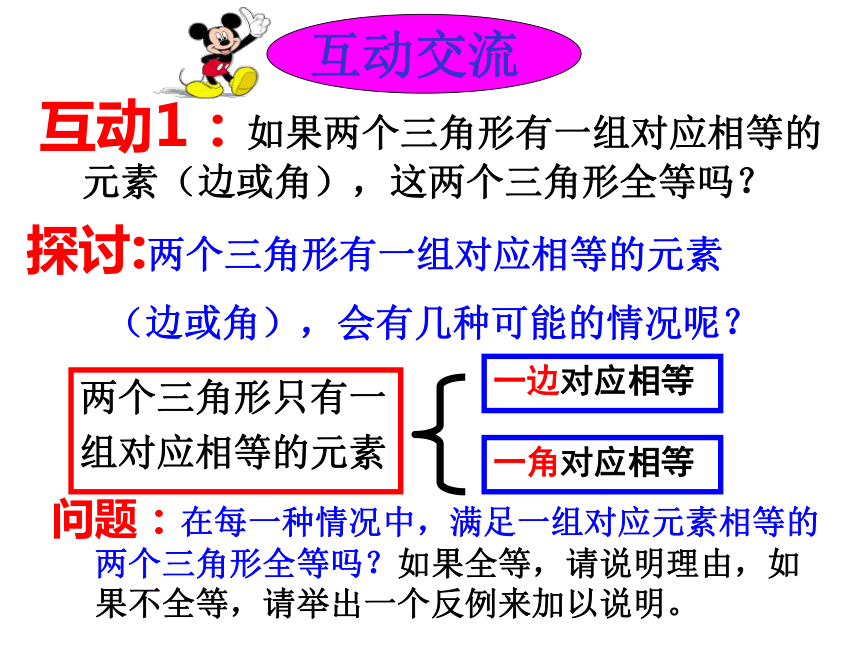
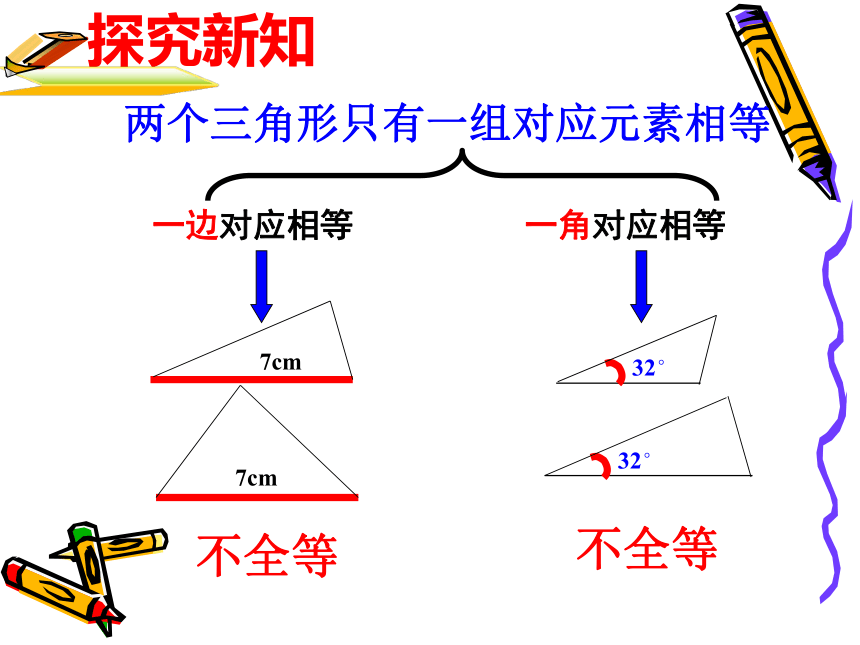
24?33?42?5?1问题:在每一种情况中,满足一组对应元素相等的两个三角形全等吗?如果全等,请说明理由,如果不全等,请举出一个反例来加以说明。不全等不全等第一组:画一个三角形,要求它的两个内角分别为30°和75°;
第二组:画一个三角形,要求三角形的两边分别为5cm和6cm;
第三组:画一个三角形,要求三角形的一个内角为30°,一条边为6cm,且这条长6cm的边是30°角的邻边;第四组:画一个三角形,要求三角形的一个内角为90°,一条边为5cm,且这条长5cm的边是90°角的对边;不全等不全等不全等不全等两个三角形有三组对应元素相等满足这些条件的三角形全等吗?作图:已知△ABC,再画一个ΔA′B′C′,使B′C′=BC, ∠ B′= ∠ B, ∠ C′= ∠ C.(同学们自己画图)。
1、画线段B′C′=BC
2、在B′C′的同旁,分别以B′、C′为顶点作∠M B′C′=∠B, ∠N C′ B′=∠C, B′M 、C′N交于点A′,得△ A′B′C′已知两角及其夹边如何作一个三角形呢?我探究现在同学们把我们所画的两个三角形重合在一起,你发现了什么?完全重合!由全等三角形定义你能得到什么结论?
如何用符号语言来表达呢?∠A=∠A AB=A B∴△ABC≌△A’B’C’(ASA)ACB′′′∠B=∠B′两角及夹边对应相等的两个三角形全等(ASA).在△ABC和△A'B'C'中, ∠A=∠A', ∠B=∠B',BC=B'C', △ABC和△A'B'C'全等吗?为什么?ACBB'A'C'探索分析:能否转化为ASA?证明:∵ ∠A=∠A', ∠B=∠B'(已知) ∴∠C=∠C'(三角形内角和定理) ∠B=∠B' 在△ABC和△A'B'C'中BC=B'C' ∠C=∠C'∴△ABC≌△A'B'C'(ASA)你能从上题中得到什么结论?两角及一角的对边对应相等的两个三角形全等(AAS)。如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A∴△ABC≌△A’B’C’(AAS)ACB′′′′∠B=∠B′ 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”(ASA)归纳解:在△ABD和△CDB中
∴ △ABD≌△CDB (ASA)
例2、已知:如图,AB为 的角平分线 ,∠ABD=∠ABC,求证:AC=AD
分析:要证AC=AD,只需证明△ACB≌△ADB,根据“ASA”即可证。证明:在△ACB和△ADB中
∴ △ACB≌△ADB (ASA)∴AC=AD∵∠CAB=∠DABAB=AB (公共边)∠ABC=∠ABD∵AB为 的角平分线 ∴∠CAB=∠DAB
三角形全等判定方法3用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了ABCDE证明:在△ABC和△DEC中CA=CD
∠ACB=∠DCE
CB=CE∴△ABC≌△DEC(SAS)∴AB=DE已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?例题推广证明:在△ABD与△CBD中AB=CB
∠ABD=∠CBD
BD=BD∴△ABD≌△CBD(SAS)∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D
.1、如图(1),AB=AC,E、F分别是AC、AB的中点,那么△ABE≌△ACF.
2、根据(1)的证明,若连结BC,如(2).请证明:△EBC≌△FCB2、如图,AB、CD均被点O平分,求证:AC=BD 如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?你能说明其中理由吗?议一议1.如图所示,有一块三角形镜子,小明不小心摔破成Ⅰ、Ⅱ两块,现需配制同样大小的镜子.为了方便起见,需带上 块即可,其理由是 .2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A、带①去 B、带②去
C、带③去 D、带①和②去 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法4应用迁移,巩固提高 例1. 如下图,△ABC是一个钢架, AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD分析:要证明△ ABD≌ △ACD,首先要看这两个三角形的三条边是否对应相等。证明: ∵D是BC中点,
∴BD=CD.
思考 已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,
还应该有AB=DF这个条件∵ DB是AB与DF的公共部分,
且AD=FB
∴ AD+DB=FB+DB
即 AB=FD思考 已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?思考 已知AC=FE,BC=DE,点A,B,D,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?ACEFDB变式再见
某检查人员到工厂检查三角形模型尺寸是否合格。其中标准模型尺寸如图,如果你是检查人员,你至少需要量出几个数据,才能判断出两个三角形模型全等呢?645βγα帮帮我探索全等三角形的判定条件(1)周长相等的两个三角形一定全等吗?想一想:想一想:(2)面积相等的两个三角形一定全等吗?∵AB =A′B′,B C=B ′ C′, AC=A ′ C ′,∴ △ABC ≌△A′B′C′(全等三角形的定义)∠A=∠A ′,∠B=∠B ′,∠C=∠C ′,(已知)AB =A′B′ ,B C=B ′ C′ , AC=A ′ C ′,且∠A=∠A ′, ∠B=∠B ′。那么 △ABC 与△A′B′C′是否全等呢?为什么?1
5
?
24?33?42?5?1问题:在每一种情况中,满足一组对应元素相等的两个三角形全等吗?如果全等,请说明理由,如果不全等,请举出一个反例来加以说明。不全等不全等第一组:画一个三角形,要求它的两个内角分别为30°和75°;
第二组:画一个三角形,要求三角形的两边分别为5cm和6cm;
第三组:画一个三角形,要求三角形的一个内角为30°,一条边为6cm,且这条长6cm的边是30°角的邻边;第四组:画一个三角形,要求三角形的一个内角为90°,一条边为5cm,且这条长5cm的边是90°角的对边;不全等不全等不全等不全等两个三角形有三组对应元素相等满足这些条件的三角形全等吗?作图:已知△ABC,再画一个ΔA′B′C′,使B′C′=BC, ∠ B′= ∠ B, ∠ C′= ∠ C.(同学们自己画图)。
1、画线段B′C′=BC
2、在B′C′的同旁,分别以B′、C′为顶点作∠M B′C′=∠B, ∠N C′ B′=∠C, B′M 、C′N交于点A′,得△ A′B′C′已知两角及其夹边如何作一个三角形呢?我探究现在同学们把我们所画的两个三角形重合在一起,你发现了什么?完全重合!由全等三角形定义你能得到什么结论?
如何用符号语言来表达呢?∠A=∠A AB=A B∴△ABC≌△A’B’C’(ASA)ACB′′′∠B=∠B′两角及夹边对应相等的两个三角形全等(ASA).在△ABC和△A'B'C'中, ∠A=∠A', ∠B=∠B',BC=B'C', △ABC和△A'B'C'全等吗?为什么?ACBB'A'C'探索分析:能否转化为ASA?证明:∵ ∠A=∠A', ∠B=∠B'(已知) ∴∠C=∠C'(三角形内角和定理) ∠B=∠B' 在△ABC和△A'B'C'中BC=B'C' ∠C=∠C'∴△ABC≌△A'B'C'(ASA)你能从上题中得到什么结论?两角及一角的对边对应相等的两个三角形全等(AAS)。如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A∴△ABC≌△A’B’C’(AAS)ACB′′′′∠B=∠B′ 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”(ASA)归纳解:在△ABD和△CDB中
∴ △ABD≌△CDB (ASA)
例2、已知:如图,AB为 的角平分线 ,∠ABD=∠ABC,求证:AC=AD
分析:要证AC=AD,只需证明△ACB≌△ADB,根据“ASA”即可证。证明:在△ACB和△ADB中
∴ △ACB≌△ADB (ASA)∴AC=AD∵∠CAB=∠DABAB=AB (公共边)∠ABC=∠ABD∵AB为 的角平分线 ∴∠CAB=∠DAB
三角形全等判定方法3用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了ABCDE证明:在△ABC和△DEC中CA=CD
∠ACB=∠DCE
CB=CE∴△ABC≌△DEC(SAS)∴AB=DE已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?例题推广证明:在△ABD与△CBD中AB=CB
∠ABD=∠CBD
BD=BD∴△ABD≌△CBD(SAS)∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D
.1、如图(1),AB=AC,E、F分别是AC、AB的中点,那么△ABE≌△ACF.
2、根据(1)的证明,若连结BC,如(2).请证明:△EBC≌△FCB2、如图,AB、CD均被点O平分,求证:AC=BD 如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?你能说明其中理由吗?议一议1.如图所示,有一块三角形镜子,小明不小心摔破成Ⅰ、Ⅱ两块,现需配制同样大小的镜子.为了方便起见,需带上 块即可,其理由是 .2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A、带①去 B、带②去
C、带③去 D、带①和②去 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法4应用迁移,巩固提高 例1. 如下图,△ABC是一个钢架, AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD分析:要证明△ ABD≌ △ACD,首先要看这两个三角形的三条边是否对应相等。证明: ∵D是BC中点,
∴BD=CD.
思考 已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,
还应该有AB=DF这个条件∵ DB是AB与DF的公共部分,
且AD=FB
∴ AD+DB=FB+DB
即 AB=FD思考 已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?思考 已知AC=FE,BC=DE,点A,B,D,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?ACEFDB变式再见
