空间直线二[上学期]
图片预览


文档简介
课件7张PPT。空间直线(二)【教学目标】
掌握定理及推论,以及公理4的应用。
【教学重点】
定理的证明。
【教学难点】
定理的证明。
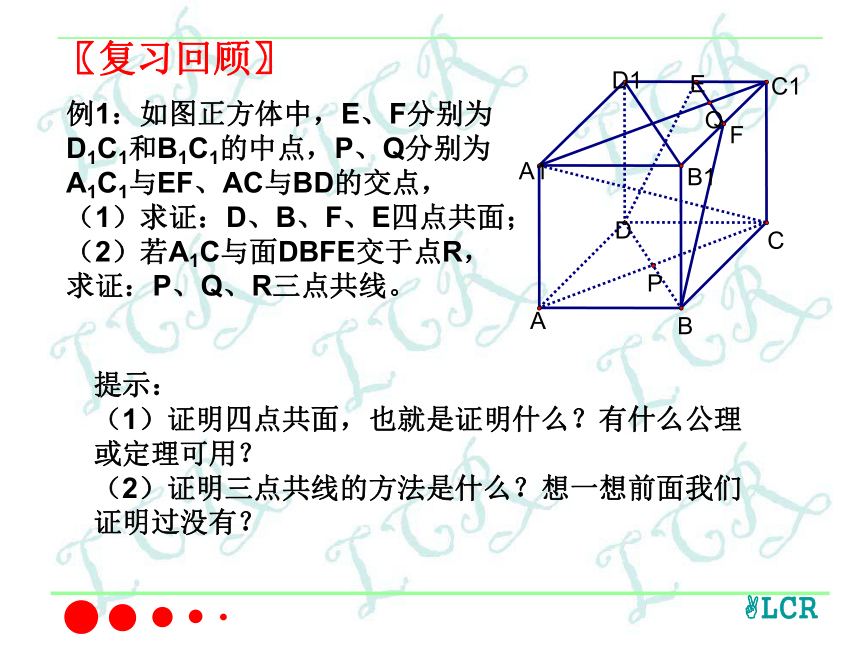
【教学过程】〖复习回顾〗例1:如图正方体中,E、F分别为D1C1和B1C1的中点,P、Q分别为A1C1与EF、AC与BD的交点,
(1)求证:D、B、F、E四点共面;
(2)若A1C与面DBFE交于点R,求证:P、Q、R三点共线。提示:
(1)证明四点共面,也就是证明什么?有什么公理或定理可用?
(2)证明三点共线的方法是什么?想一想前面我们证明过没有?例2:如图,空间四边形ABCD中,E、F分别为BC、CD的中点,G、H分别为AB、AD上的点,且AG:GB≠AH:HD
证明:GH与EF为异面直线。提示:什么叫异面直线?其相对的线线位置关系是什么?
考虑:(1)如果直接证明,就必须证明GH和EF不在同一平面内,有这样的定理或公理吗?
(2)从(1)知,正面证明是不可取,那么我们可以考虑从反而来考虑——平行或相交。【二、新课】
初中我们学过,如果一个角的两边分别平行另一个角的两边,那么这两个角的关系如何?
引申:如果在空间的两个角的两边分别平行,且方向相同那么这两个角的关系又是什么样的呢?〖定理〗如果一个角的两边和另一个角的两边分别平行,且方向相同,那么这两个角相等。要求:(1)自己动手画图。
(2)写出已知、求证。
(3)考虑如何证明两个角相等?〖推论〗 :如果两条相交直线和另两条相交直线分别平行,那么这两组相交直线所成的锐角(或直角)相等。观看动画【三练习】1、在正方体ABCD-A’B’C’D’中,表面的对角线中与AD’成600的角有( )
(A)4条 (B)6条 (C)8条 (D)10条2、如图,立体图形A-BCD的4个面分别是△ABC,△ABD,△BCD,E、FG分别为线段AB、AC、AD上的点,EF∥BC,FG∥CD, △EFG和△BCD有什么关系,证明你的结论。【作业】P15页 7,8,9题
掌握定理及推论,以及公理4的应用。
【教学重点】
定理的证明。
【教学难点】
定理的证明。
【教学过程】〖复习回顾〗例1:如图正方体中,E、F分别为D1C1和B1C1的中点,P、Q分别为A1C1与EF、AC与BD的交点,
(1)求证:D、B、F、E四点共面;
(2)若A1C与面DBFE交于点R,求证:P、Q、R三点共线。提示:
(1)证明四点共面,也就是证明什么?有什么公理或定理可用?
(2)证明三点共线的方法是什么?想一想前面我们证明过没有?例2:如图,空间四边形ABCD中,E、F分别为BC、CD的中点,G、H分别为AB、AD上的点,且AG:GB≠AH:HD
证明:GH与EF为异面直线。提示:什么叫异面直线?其相对的线线位置关系是什么?
考虑:(1)如果直接证明,就必须证明GH和EF不在同一平面内,有这样的定理或公理吗?
(2)从(1)知,正面证明是不可取,那么我们可以考虑从反而来考虑——平行或相交。【二、新课】
初中我们学过,如果一个角的两边分别平行另一个角的两边,那么这两个角的关系如何?
引申:如果在空间的两个角的两边分别平行,且方向相同那么这两个角的关系又是什么样的呢?〖定理〗如果一个角的两边和另一个角的两边分别平行,且方向相同,那么这两个角相等。要求:(1)自己动手画图。
(2)写出已知、求证。
(3)考虑如何证明两个角相等?〖推论〗 :如果两条相交直线和另两条相交直线分别平行,那么这两组相交直线所成的锐角(或直角)相等。观看动画【三练习】1、在正方体ABCD-A’B’C’D’中,表面的对角线中与AD’成600的角有( )
(A)4条 (B)6条 (C)8条 (D)10条2、如图,立体图形A-BCD的4个面分别是△ABC,△ABD,△BCD,E、FG分别为线段AB、AC、AD上的点,EF∥BC,FG∥CD, △EFG和△BCD有什么关系,证明你的结论。【作业】P15页 7,8,9题
