沪教版(五四学制)七年级下册15.2直角坐标平面内点的运动(第3课时)课件(共20张PPT)
文档属性
| 名称 | 沪教版(五四学制)七年级下册15.2直角坐标平面内点的运动(第3课时)课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 581.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
2022-2023学年七年级数学下册同步精品课堂(沪教版)
第 15章平面直角坐标系
15.2直角坐标平面内点的运动(第3课时)
探究2
在直角坐标平面内,与点 M(,y) 关于 轴或y轴对称的点的坐标是什么
操作2
在直角坐标平面内,描出点 A(-3,2),再描出与点 A 关于x轴对称的点 B,与点A 关于r轴对称的点C,如图15-14所示。利用两个点关于一直线对称的性质,可知点 B 的坐标是(-3,-2),点 C 的坐标是(3,2).
一般地,在直角坐标平面内,
与点 M(x,y)关于 x轴对称的点的坐标为(x,-y);
与点 M(x,y)关于 y轴对称的点的坐标为(-x,y).
口答
(1)点M(-2,-3)关于x轴对称的点的坐标是_____;
(2)点N(0,- )关于x轴对称的点的坐标是______ ;
(-2,3)
(0, )
口答
(1)点P(1,-4)关于y轴对称的点的坐标是______;
(2)点Q(x,0)关于y轴对称的点的坐标是______;
(-1,-4)
(-x,0)
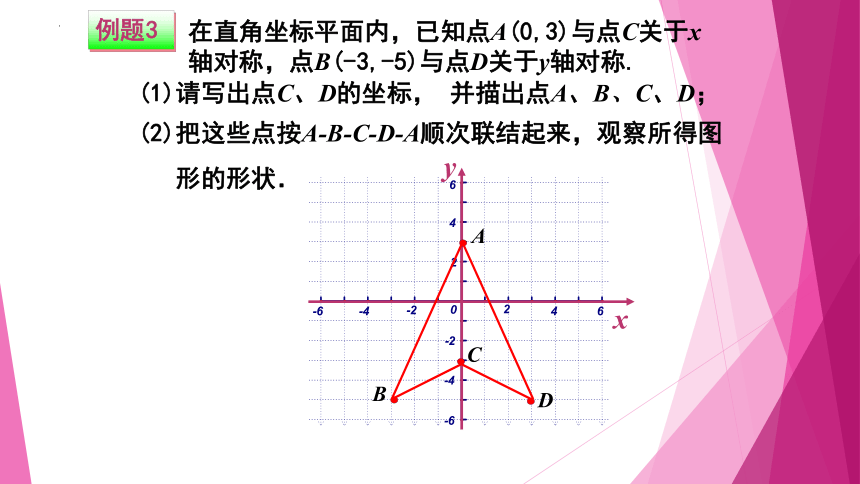
在直角坐标平面内,已知点A(0,3)与点C关于x轴对称,点B(-3,-5)与点D关于y轴对称.
x
y
A
B
(2)把这些点按A-B-C-D-A顺次联结起来,观察所得图
形的形状.
(1)请写出点C、D的坐标, 并描出点A、B、C、D;
例题3
D
C
探究3
在直角坐标平面内,与点M(x,y) 关于原点对称的点的坐标是什么
操作3
在直角坐标平面内,描出点 A(-3,2),再描出与点 A 关于原点 0 对称的点 B,如图15-16所示。分别过点 A、B作x轴的垂线,垂足分别为A‘、B.因为 OA’=B‘(为什么 ),所以点A与点 B 的横坐标瓦为相反数;同样,点A与点 B 的纵坐标也互为相反数。于是得到点 B 的坐标是(3,2).
口答
(1)点G(-6,8)关于原点对称的点的坐标是____ ;
(2)点H(2.5,0)关于原点对称的点的坐标是____ ;
(6,-8)
(-2.5,0)
一般地,在直角坐标平面内,与点 M(x,y)关于原点对称的点的坐标为(-x,-y).
F1
F2
A
B
C
D
E
F
F4
F3
例题4 如图,是一个风车的图案,F1、F2、F3 、F4表示风车的四个叶片,图案是一个中心对称图形,点O是对称中心.
试在右图中画出风车图案 .
平面直角坐标系内对称点的坐标的特点:
1、关于x轴对称的两点,横坐标相同,纵坐标互为相反数。
2、关于y轴对称的两点,纵坐标相同,横坐标互为相反数。
3、关于原点对称的两点,横纵坐标都互为相反数。
(6)点M(0,-7)关于y轴对称的点N的坐标是______;
(1)点M(1,-4)关于y轴对称的点N的坐标是______;
(2)点M(-2,-3)关于x轴对称的点N的坐标是_____;
快速抢答
(3)点M(-6,-8)关于原点对称的点N的坐标是____;
(4)点M(0,4)关于x轴对称的点N的坐标是_______;
(5)点M(-5,0)关于y轴对称的点N的坐标是______;
(-1,-4)
(-2,3)
(6,8)
(0,-4)
(5,0)
(0,-7)
(12)点G(4,0)与点H(-4,0)关于_________对称.
(7)点M(-2,3)与点N(2,3)关于______对称;
(8)点E ______与点F(5,4)关于x轴对称;
(9)点A(-2,-4)与点B(2,4)关于______对称;
(10)点E ______与点F(0,-3)关于y轴对称;
(11)点G ______与点H(-5,0)关于原点对称;
y 轴
(5,-4)
原点
(0,-3)
y 轴或原点
(5,0)
快速抢答
课本练习
1. 口答:
(1)与点 P(-4,-V2)关于x 轴对称的点的坐标是
(2) 与点 Q(V3,-1)关于y轴对称的点的坐标是
(3) 与点 M(0,-2)关于x 轴对称的点的坐标是
(4)与点 N(,0)关于轴对称的点的坐标是
2.在右图中,画出△ABC 分别关于 轴y 轴对称的图形△A1B1C1和△A2B2C2,再写出各个三角形的顶点坐标
3. 口答:
(1) 与点 P(-4,3)关于原点 0 对称的点的坐标是
(4)与点N(x,y)关于原点0 对称的点的坐标是
(5) 如果点A 在第三象限,那么与点A 关于原点0对称的点在
第 象限
(6) 如果点 B在x轴的正半轴上,那么与点 B 关于原点0 对称的
点在 。
4.如图,画出四边形 OABC 关于原点 0 对称的四边形 OABG,再写出这两个四边形的顶点坐标.
x
y
5.如图所示的平面直角坐标系内,有标记为甲、乙、丙、丁的四个三角形.
甲
丁
丙
乙
(2,5)
(-2,5)
(3,1)
(-3,1)
(4,2)
(-4,2)
(-3,-1)
(-4,-2)
(-2,-5)
(1)哪两个三角形关于y轴对称?
(2)哪两个三角形关于x轴对称?
(3)哪两个三角形关于原点对称?
(4)哪个三角形经过怎样的平移可以得到另一个三角形?
随堂检测
(3)点G(4,0)与点H(-4,0)关于_________对称.
(1)点M(2,-3)与点N(2,3)关于______对称;
(2)点A(-2,-4)与点B(2,4)关于______对称;
x 轴
原点
y 轴或原点
(4)点E ______与点F(5,4)关于x轴对称;
(5)点E ______与点F(0,-3)关于y轴对称;
(6)点G ______与点H(-5,0)关于原点对称;
(5,-4)
(0,-3)
(5,0)
2022-2023学年七年级数学下册同步精品课堂(沪教版)
第 15章平面直角坐标系
15.2直角坐标平面内点的运动(第3课时)
探究2
在直角坐标平面内,与点 M(,y) 关于 轴或y轴对称的点的坐标是什么
操作2
在直角坐标平面内,描出点 A(-3,2),再描出与点 A 关于x轴对称的点 B,与点A 关于r轴对称的点C,如图15-14所示。利用两个点关于一直线对称的性质,可知点 B 的坐标是(-3,-2),点 C 的坐标是(3,2).
一般地,在直角坐标平面内,
与点 M(x,y)关于 x轴对称的点的坐标为(x,-y);
与点 M(x,y)关于 y轴对称的点的坐标为(-x,y).
口答
(1)点M(-2,-3)关于x轴对称的点的坐标是_____;
(2)点N(0,- )关于x轴对称的点的坐标是______ ;
(-2,3)
(0, )
口答
(1)点P(1,-4)关于y轴对称的点的坐标是______;
(2)点Q(x,0)关于y轴对称的点的坐标是______;
(-1,-4)
(-x,0)
在直角坐标平面内,已知点A(0,3)与点C关于x轴对称,点B(-3,-5)与点D关于y轴对称.
x
y
A
B
(2)把这些点按A-B-C-D-A顺次联结起来,观察所得图
形的形状.
(1)请写出点C、D的坐标, 并描出点A、B、C、D;
例题3
D
C
探究3
在直角坐标平面内,与点M(x,y) 关于原点对称的点的坐标是什么
操作3
在直角坐标平面内,描出点 A(-3,2),再描出与点 A 关于原点 0 对称的点 B,如图15-16所示。分别过点 A、B作x轴的垂线,垂足分别为A‘、B.因为 OA’=B‘(为什么 ),所以点A与点 B 的横坐标瓦为相反数;同样,点A与点 B 的纵坐标也互为相反数。于是得到点 B 的坐标是(3,2).
口答
(1)点G(-6,8)关于原点对称的点的坐标是____ ;
(2)点H(2.5,0)关于原点对称的点的坐标是____ ;
(6,-8)
(-2.5,0)
一般地,在直角坐标平面内,与点 M(x,y)关于原点对称的点的坐标为(-x,-y).
F1
F2
A
B
C
D
E
F
F4
F3
例题4 如图,是一个风车的图案,F1、F2、F3 、F4表示风车的四个叶片,图案是一个中心对称图形,点O是对称中心.
试在右图中画出风车图案 .
平面直角坐标系内对称点的坐标的特点:
1、关于x轴对称的两点,横坐标相同,纵坐标互为相反数。
2、关于y轴对称的两点,纵坐标相同,横坐标互为相反数。
3、关于原点对称的两点,横纵坐标都互为相反数。
(6)点M(0,-7)关于y轴对称的点N的坐标是______;
(1)点M(1,-4)关于y轴对称的点N的坐标是______;
(2)点M(-2,-3)关于x轴对称的点N的坐标是_____;
快速抢答
(3)点M(-6,-8)关于原点对称的点N的坐标是____;
(4)点M(0,4)关于x轴对称的点N的坐标是_______;
(5)点M(-5,0)关于y轴对称的点N的坐标是______;
(-1,-4)
(-2,3)
(6,8)
(0,-4)
(5,0)
(0,-7)
(12)点G(4,0)与点H(-4,0)关于_________对称.
(7)点M(-2,3)与点N(2,3)关于______对称;
(8)点E ______与点F(5,4)关于x轴对称;
(9)点A(-2,-4)与点B(2,4)关于______对称;
(10)点E ______与点F(0,-3)关于y轴对称;
(11)点G ______与点H(-5,0)关于原点对称;
y 轴
(5,-4)
原点
(0,-3)
y 轴或原点
(5,0)
快速抢答
课本练习
1. 口答:
(1)与点 P(-4,-V2)关于x 轴对称的点的坐标是
(2) 与点 Q(V3,-1)关于y轴对称的点的坐标是
(3) 与点 M(0,-2)关于x 轴对称的点的坐标是
(4)与点 N(,0)关于轴对称的点的坐标是
2.在右图中,画出△ABC 分别关于 轴y 轴对称的图形△A1B1C1和△A2B2C2,再写出各个三角形的顶点坐标
3. 口答:
(1) 与点 P(-4,3)关于原点 0 对称的点的坐标是
(4)与点N(x,y)关于原点0 对称的点的坐标是
(5) 如果点A 在第三象限,那么与点A 关于原点0对称的点在
第 象限
(6) 如果点 B在x轴的正半轴上,那么与点 B 关于原点0 对称的
点在 。
4.如图,画出四边形 OABC 关于原点 0 对称的四边形 OABG,再写出这两个四边形的顶点坐标.
x
y
5.如图所示的平面直角坐标系内,有标记为甲、乙、丙、丁的四个三角形.
甲
丁
丙
乙
(2,5)
(-2,5)
(3,1)
(-3,1)
(4,2)
(-4,2)
(-3,-1)
(-4,-2)
(-2,-5)
(1)哪两个三角形关于y轴对称?
(2)哪两个三角形关于x轴对称?
(3)哪两个三角形关于原点对称?
(4)哪个三角形经过怎样的平移可以得到另一个三角形?
随堂检测
(3)点G(4,0)与点H(-4,0)关于_________对称.
(1)点M(2,-3)与点N(2,3)关于______对称;
(2)点A(-2,-4)与点B(2,4)关于______对称;
x 轴
原点
y 轴或原点
(4)点E ______与点F(5,4)关于x轴对称;
(5)点E ______与点F(0,-3)关于y轴对称;
(6)点G ______与点H(-5,0)关于原点对称;
(5,-4)
(0,-3)
(5,0)
