点到线的距离[上学期]

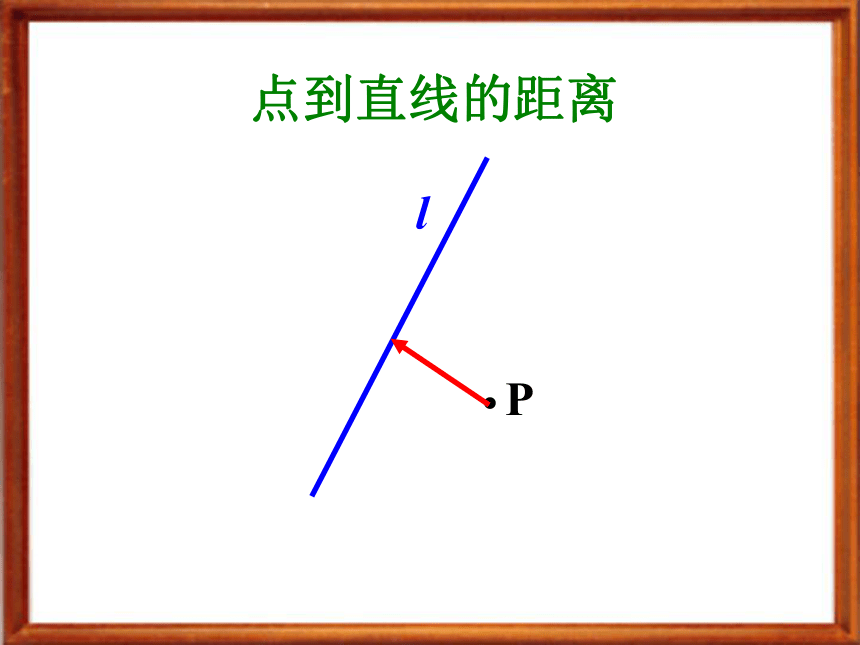
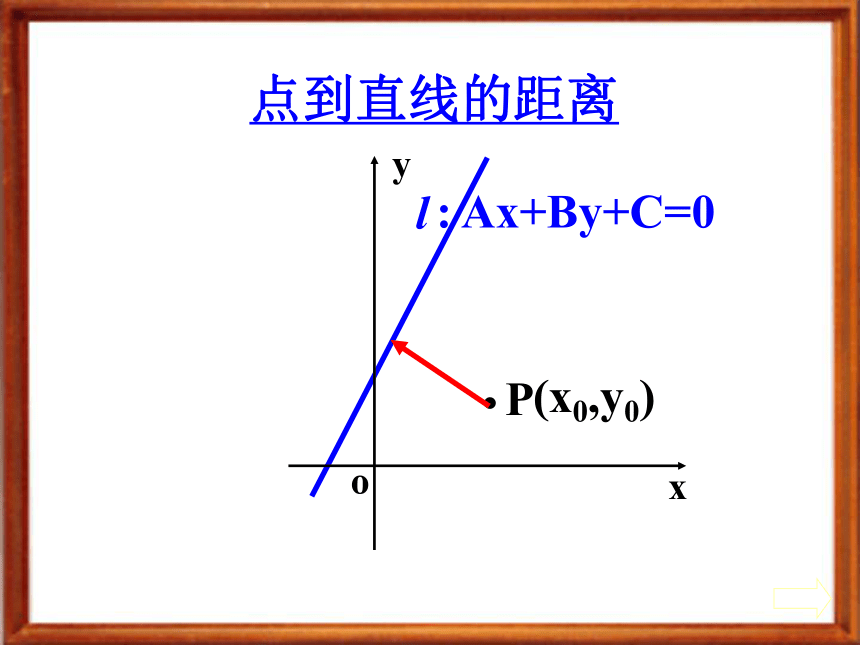
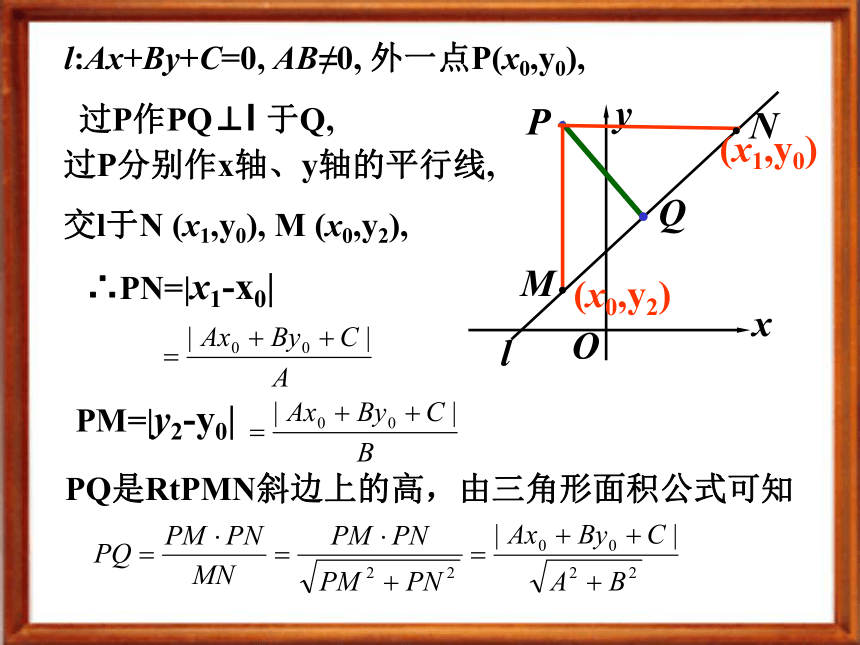
课件16张PPT。点到直线的距离姜堰二中高一数学组 张金龙学校铁路点到直线的距离llP.: Ax+By+C=0(x0,y0)点到直线的距离确定直线l的斜率k求与l垂直直线的斜率k′ 求过点P垂直于l的直线l′的方程求l与l ′的交点H 求点P与点H的距离 得到点P到l的距离d算法流程图 点评：点到直线的距离转化为点到点的距离Oyxll:Ax+By+C=0, AB≠0, 外一点P(x0,y0), (x1,y0)(x0,y2)过P作PQ⊥l 于Q,过P分别作x轴、y轴的平行线,
交l于N (x1,y0), M (x0,y2), ∴PN=|x1-x0|PM=|y2-y0|PQ是RtPMN斜边上的高，由三角形面积公式可知已知点P(x0, y0)和直线l:Ax+By+C=0.则P点到直线 l 的距离d为:点到直线的距离公式2.求两平行直线l1: 2x-7y+8=0yOxl2: 2x－7y－6=0l1:2x－7y+8=0 两平行直线间的距离转化为点到直线的距离l2: 2x-7y-6=0 间的距离.课堂练习直线的方程应化为一般式！点 到 直 线 的 距 离1.此公式的作用是求点到直线的距离；2.此公式是在A、B≠0的前提下推导的；3.如果A=0或B=0，此公式恰好也成立；4.如果A=0或B=0，一般不用此公式；5.用此公式时直线要先化成一般式。⑴应用理解：补全过程证明:建立如图直角坐标系,设P (x,0),x∈( )可求得lAB:( )lCB:( )|PE|=( )|PF|=( )A到BC的距离h=( )因为|PE|+|PF|=h，所以原命题得证。要求：1.掌握点到直线的距离公式的推导过程；2.能用点到直线的距离公式进行计算；3.能求有关平行线间的距离。自我检测作 业且与它距离为 的直线方程.用解析法证明:等腰三角形底边延长 线上一点到两腰所在直线的距离之差等于一腰上的高. 3. 求平行直线 l1: Ax+By+C1=01. 求平行于直线x－y－2=0 l2: Ax+By+C2=0的距离.欢迎大家提出宝贵意见！谢谢点到直线的距离