2014年快乐暑假初三数学衔接班——二元一次方程组(第2课时)
文档属性
| 名称 | 2014年快乐暑假初三数学衔接班——二元一次方程组(第2课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 68.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-07 00:00:00 | ||
图片预览


文档简介
2014年快乐暑假初三数学衔接班——二元一次方程组(第2课时)
一.选择题(共3小题)
1.(2014 泰安)方程5x+2y=﹣9与下列方程构成的方程组的解为的是( )
A. x+2y=1 B. 3x+2y=﹣8 C. 5x+4y=﹣3 D. 3x﹣4y=﹣8
2.(2011 泰安)某班为奖励在校运会 ( http: / / www.21cnjy.com )上取得较好成绩的运动员,花了400元钱购买甲.乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种各买多少件?该问题中,若设购买甲种奖品x件,乙种奖品y件,则列方程正确的是( )
A. B.
C. D.
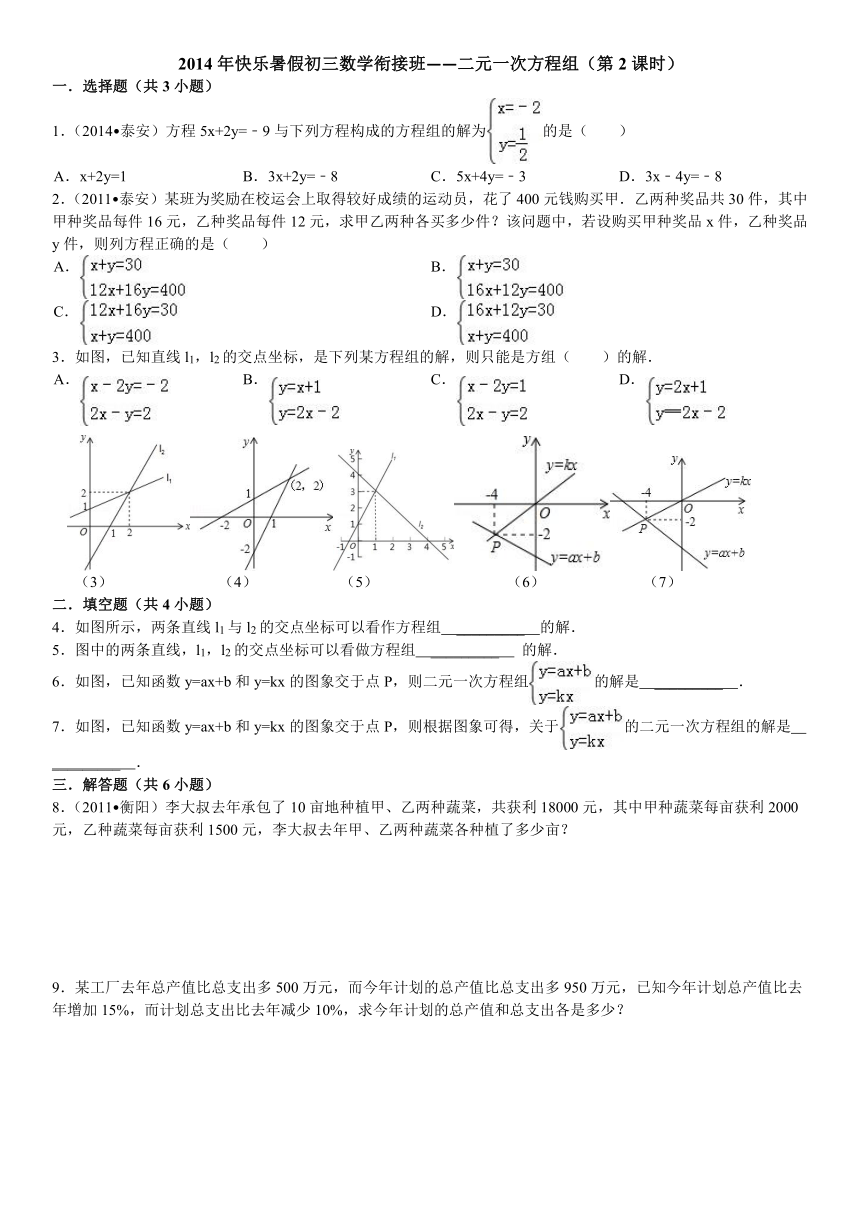
3.如图,已知直线l1,l2的交点坐标,是下列某方程组的解,则只能是方组( )的解.
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (4) ( http: / / www.21cnjy.com ) (5) (6) (7)
二.填空题(共4小题)
4.如图所示,两条直线l1与l2的交点坐标可以看作方程组 _________ 的解.
5.图中的两条直线,l1,l2的交点坐标可以看做方程组 _________ 的解.
6.如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组的解是 _________ .
7.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于的二元一次方程组的解是 _________ .
三.解答题(共6小题)
8.(2011 衡阳)李大叔去年承包了10 ( http: / / www.21cnjy.com )亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?
9.某工厂去年总产值比总支 ( http: / / www.21cnjy.com )出多500万元,而今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求今年计划的总产值和总支出各是多少?
10.(2011 烟台)小华从家里到学 ( http: / / www.21cnjy.com )校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?
11.一个两位数,个位数字比十位数字大5,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是143.求原来的两位数.
12.(2012 黔东南州)解方程组 ( http: / / www.21cnjy.com ). 13.解方程组:.
14、 ( http: / / www.21cnjy.com ) 15、 HYPERLINK "http://www.21cnjy.com"
2014年快乐暑假初三数学衔接复习部分——二元一次方程组第2课时
参考答案与试题解析
一.选择题(共3小题)
1.D2.B.3.A.
二.填空题(共4小题)
4.5..6..7. .
三.解答题(共6小题)
8.解:设甲、乙两种蔬菜各种植了x、y亩,依题意得:
,
解得:,
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
9.解:设去年计划的总产值是x万元,则总支出(x﹣500)万元.
根据题意,得(1+15%)x﹣(1﹣10%)(x﹣500)=950,
解得:x=2000,
∴x﹣500=1500,
则(1+15%)×2000=2300,(1﹣10%)×1500=1350.
答:今年计划的总产值为2300万元,总支出为1350万元.
10.解:设平路有x米,坡路有y米,根据题意列方程得,
( http: / / www.21cnjy.com ),
解这个方程组,得,
所以x+y=700.
所以小华家离学校700米.
11.解:设个位数字为x,十位数字为y,
由题意得,,
解得:,
即原来的两位数是49.
12.
解: ( http: / / www.21cnjy.com )
③+①得,3x+5y=11④,
③×2+②得,3x+3y=9⑤,
④﹣⑤得2y=2,y=1,
将y=1代入⑤得,3x=6,
x=2,
将x=2,y=1代入①得,z=6﹣2×2﹣3×1=﹣1,
∴方程组的解为.
13. 解:把③代入①得,5y+z=12④,
把③代入②得,6y+5z=22⑤,
④×5﹣⑤,得19y=38,
解得y=2,
把y=2代入④得z=2,
把把y=2,z=2代入①,得x+2+2=12,
解得x=8,
故原方程组的解为:
14、
15、:
一.选择题(共3小题)
1.(2014 泰安)方程5x+2y=﹣9与下列方程构成的方程组的解为的是( )
A. x+2y=1 B. 3x+2y=﹣8 C. 5x+4y=﹣3 D. 3x﹣4y=﹣8
2.(2011 泰安)某班为奖励在校运会 ( http: / / www.21cnjy.com )上取得较好成绩的运动员,花了400元钱购买甲.乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种各买多少件?该问题中,若设购买甲种奖品x件,乙种奖品y件,则列方程正确的是( )
A. B.
C. D.
3.如图,已知直线l1,l2的交点坐标,是下列某方程组的解,则只能是方组( )的解.
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (4) ( http: / / www.21cnjy.com ) (5) (6) (7)
二.填空题(共4小题)
4.如图所示,两条直线l1与l2的交点坐标可以看作方程组 _________ 的解.
5.图中的两条直线,l1,l2的交点坐标可以看做方程组 _________ 的解.
6.如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组的解是 _________ .
7.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于的二元一次方程组的解是 _________ .
三.解答题(共6小题)
8.(2011 衡阳)李大叔去年承包了10 ( http: / / www.21cnjy.com )亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?
9.某工厂去年总产值比总支 ( http: / / www.21cnjy.com )出多500万元,而今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求今年计划的总产值和总支出各是多少?
10.(2011 烟台)小华从家里到学 ( http: / / www.21cnjy.com )校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?
11.一个两位数,个位数字比十位数字大5,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是143.求原来的两位数.
12.(2012 黔东南州)解方程组 ( http: / / www.21cnjy.com ). 13.解方程组:.
14、 ( http: / / www.21cnjy.com ) 15、 HYPERLINK "http://www.21cnjy.com"
2014年快乐暑假初三数学衔接复习部分——二元一次方程组第2课时
参考答案与试题解析
一.选择题(共3小题)
1.D2.B.3.A.
二.填空题(共4小题)
4.5..6..7. .
三.解答题(共6小题)
8.解:设甲、乙两种蔬菜各种植了x、y亩,依题意得:
,
解得:,
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
9.解:设去年计划的总产值是x万元,则总支出(x﹣500)万元.
根据题意,得(1+15%)x﹣(1﹣10%)(x﹣500)=950,
解得:x=2000,
∴x﹣500=1500,
则(1+15%)×2000=2300,(1﹣10%)×1500=1350.
答:今年计划的总产值为2300万元,总支出为1350万元.
10.解:设平路有x米,坡路有y米,根据题意列方程得,
( http: / / www.21cnjy.com ),
解这个方程组,得,
所以x+y=700.
所以小华家离学校700米.
11.解:设个位数字为x,十位数字为y,
由题意得,,
解得:,
即原来的两位数是49.
12.
解: ( http: / / www.21cnjy.com )
③+①得,3x+5y=11④,
③×2+②得,3x+3y=9⑤,
④﹣⑤得2y=2,y=1,
将y=1代入⑤得,3x=6,
x=2,
将x=2,y=1代入①得,z=6﹣2×2﹣3×1=﹣1,
∴方程组的解为.
13. 解:把③代入①得,5y+z=12④,
把③代入②得,6y+5z=22⑤,
④×5﹣⑤,得19y=38,
解得y=2,
把y=2代入④得z=2,
把把y=2,z=2代入①,得x+2+2=12,
解得x=8,
故原方程组的解为:
14、
15、:
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
