直线的位置关系(复习)[上学期]
图片预览



文档简介
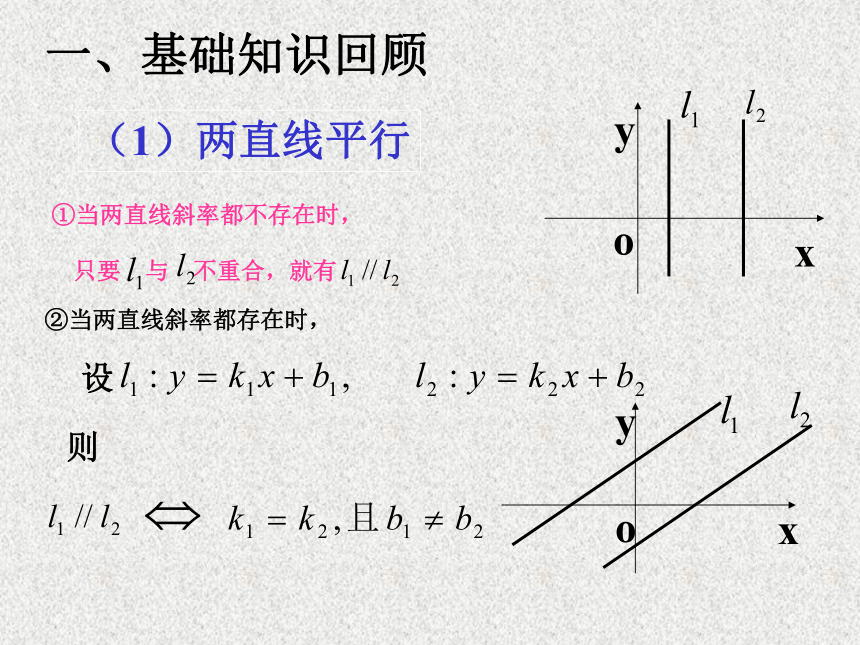
课件13张PPT。两条直线的位置关系--复习一、基础知识回顾(1)两直线平行①当两直线斜率都不存在时,②当两直线斜率都存在时,
设则(2)两直线垂直 ①两直线中有一条斜率不存在时,另一条直线的斜率为0②当两直线斜率都存在时,
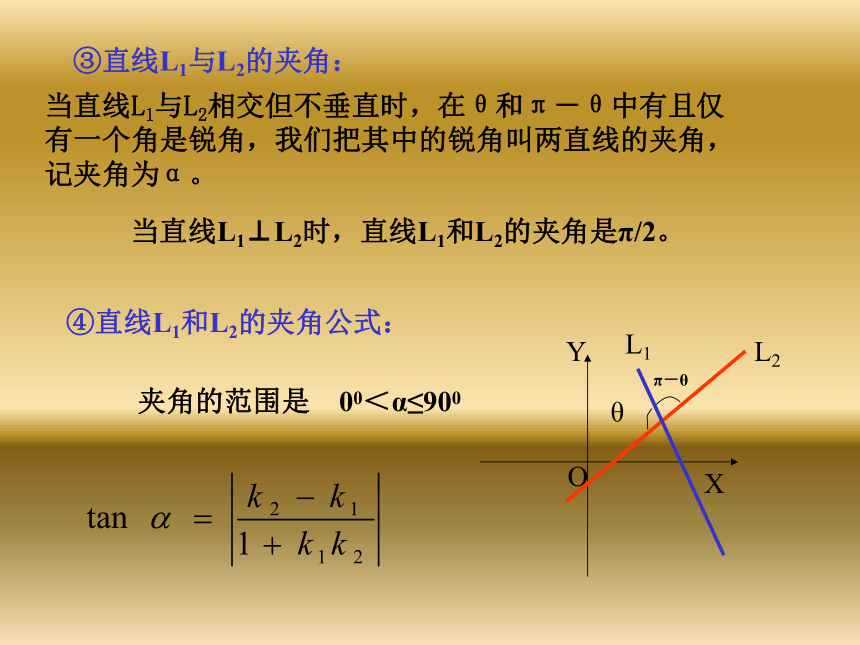
设为k1, k2θ1L1L2θ2①直线L1到L2的角:直线L1按逆时针方向旋转到与L2重合时所转的角,叫做L1到L2的角。图中θ1是L1到L2的角,θ2是L2到L1的角。(3)两直线的夹角②直线L1到L2的角公式:③直线L1与L2的夹角:当直线L1与L2相交但不垂直时,在θ和π-θ中有且仅
有一个角是锐角,我们把其中的锐角叫两直线的夹角,
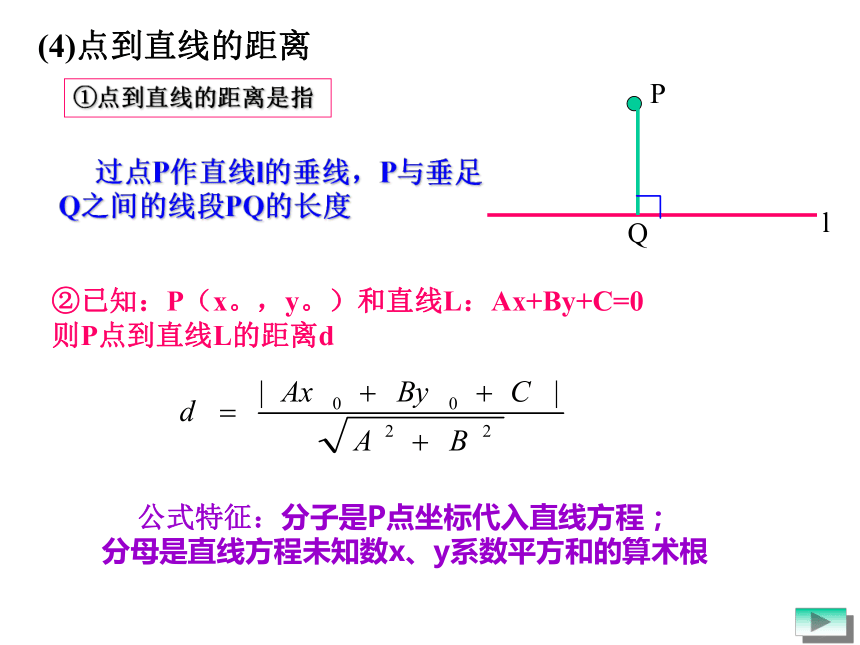
记夹角为α。当直线L1⊥L2时,直线L1和L2的夹角是π/2。④直线L1和L2的夹角公式:夹角的范围是 00<α≤900 过点P作直线l的垂线,P与垂足Q之间的线段PQ的长度①点到直线的距离是指PlQ(4)点到直线的距离公式特征:分子是P点坐标代入直线方程;
分母是直线方程未知数x、y系数平方和的算术根
②已知:P(x。,y。)和直线L:Ax+By+C=0 则P点到直线L的距离d例1.设a,b,c 分别是⊿ABC中∠A、∠B、∠C所对边的边长.
则直线L1: xsinA + ay + c =0 和直线L2: bx-ysinB+ sinC = 0
的位置关系是( ).
A .平行 B. 重合 C.垂直 D.相交但不垂直解:二.重要题型剖析直线L1的斜率直线L2的斜率由正弦定理知所以直线L1和直线L2垂直,故选C例2:已知两直线L1: x+a2y+6=0,
L2:(a-2)x+3ay+2a=0,
问a为何值时L1与L2(1)平行(2)重合(3)相交解:(1)若a=0时,L1:x+6=0 L2:x=0,所以L1∥L2①当a=3时,L1: x+9y+6=0 L2 : x+9y+6=0∴L1、L2重合②当a=-1,L1: x+y+6=0 L2 : -3x-3y-2=0 ∴ L1、L2平行③当a≠3,a≠-1,a≠0时,L1、L2相交综合上述:当a=0或-1时L1与L2平行;当a=3时L1与L2重合;当a≠3,a≠-1,a≠0时,L1、L2相交例4.已知△ABC的三边方程分别是AB:4x-3y+10=0,
BC:y-2=0,CA:3x-4y-5=0
(1)求∠B的大小.
(2) 求∠BAC的内角平分线所在直线方程.
(3)求AB边上的高所在的直线方程.解:(1)∠B是直线BA到BC的角(2)设P(x,y)为∠BAC的内角平分线所在直线上任意一点解得7x-7y+5=0或x+y+15=0由图形知7x-7y+5=0为所求(3)设AB边上的高所在的直线方程为3x-4y-5+λ(y-2)=0即3x-(4- λ)y-(5+2 λ)=0由直线垂直的充要条件,得解得λ=8所以所求直线方程是3x+4y-21=0例5. 正方形的中心为(-6,3),它的一边所在直线方程为5x+12y+7=0,求其它边所在直线方程。解:设正方形ABCD的边AB的方程是5x+12y+7=0∵CD∥AB ,∴CD边所在直线方程设为5x+12y+m=0(m≠7)∵正方形的中心P(-6,3)到直线5x+12y+7=0的距离d∴正方形的中心P到直线CD的距离是1∴直线CD的方程是5x+12y-19=0又AD、CB与直线AB垂直,可设AD、BC的方程是12x-5y+n=0∴AD、BC的方程是12x-5y+100=0或12x-5y+74=0例6.求直线a:2x+y-4=0关于直线L:3x+4y-1=0对称的直线b的方程分析:由平面几何知识,若直线a、b关于直线L对称,它们有下列几何性质:①若a、b相交,则L是a、b交角的平分线。②若点A在直线a上,那么,点A关于直线L的对称点B一定在直线b上,这时AB⊥L,且AB中点D在L上。解:解得a与L的交点E(3,-2),且点E在直线b上解法一:设直线b的斜率是k,又知a的斜率是-2,L的斜率是所以直线b的方程是即2x+11y+16=0求直线a:2x+y-4=0关于直线L:3x+4y-1=0对称的直线b的方程解法二:在直线a上取一点A(2,0),设点A关于直线L的对称点B的坐标是(x0,y0)AB则直线AB的方程是即4x-3y-8=0解得AB和L的交点M的坐标由中点坐标公式所以直线b的方程是∴b的方程是2x+11y+16=0例7.已知直线l经过点P(2,3),且和两条平行直线:3x+4y+8=0,3x+4y-7=0 分别交于A、B两点,且|AB|= 求直线l的方程分析 所求直线l经过点P(2,3),要想使问题解决,或求出它的斜率,或者再找到一个位于直线l上的点,此题难点是如何将条件|AB|= 转化为有用的信息
解:两条平行直线:3x+4y+8=0,3x+4y-7=0之间的距离因为|AB|=所以直线l与3x+4y+8=0的夹角是45o设直线l的斜率为k.则有即7x+y-17=0或x-7y+19=03x+4y+8=03x+4y-7=0BPA
设则(2)两直线垂直 ①两直线中有一条斜率不存在时,另一条直线的斜率为0②当两直线斜率都存在时,
设为k1, k2θ1L1L2θ2①直线L1到L2的角:直线L1按逆时针方向旋转到与L2重合时所转的角,叫做L1到L2的角。图中θ1是L1到L2的角,θ2是L2到L1的角。(3)两直线的夹角②直线L1到L2的角公式:③直线L1与L2的夹角:当直线L1与L2相交但不垂直时,在θ和π-θ中有且仅
有一个角是锐角,我们把其中的锐角叫两直线的夹角,
记夹角为α。当直线L1⊥L2时,直线L1和L2的夹角是π/2。④直线L1和L2的夹角公式:夹角的范围是 00<α≤900 过点P作直线l的垂线,P与垂足Q之间的线段PQ的长度①点到直线的距离是指PlQ(4)点到直线的距离公式特征:分子是P点坐标代入直线方程;
分母是直线方程未知数x、y系数平方和的算术根
②已知:P(x。,y。)和直线L:Ax+By+C=0 则P点到直线L的距离d例1.设a,b,c 分别是⊿ABC中∠A、∠B、∠C所对边的边长.
则直线L1: xsinA + ay + c =0 和直线L2: bx-ysinB+ sinC = 0
的位置关系是( ).
A .平行 B. 重合 C.垂直 D.相交但不垂直解:二.重要题型剖析直线L1的斜率直线L2的斜率由正弦定理知所以直线L1和直线L2垂直,故选C例2:已知两直线L1: x+a2y+6=0,
L2:(a-2)x+3ay+2a=0,
问a为何值时L1与L2(1)平行(2)重合(3)相交解:(1)若a=0时,L1:x+6=0 L2:x=0,所以L1∥L2①当a=3时,L1: x+9y+6=0 L2 : x+9y+6=0∴L1、L2重合②当a=-1,L1: x+y+6=0 L2 : -3x-3y-2=0 ∴ L1、L2平行③当a≠3,a≠-1,a≠0时,L1、L2相交综合上述:当a=0或-1时L1与L2平行;当a=3时L1与L2重合;当a≠3,a≠-1,a≠0时,L1、L2相交例4.已知△ABC的三边方程分别是AB:4x-3y+10=0,
BC:y-2=0,CA:3x-4y-5=0
(1)求∠B的大小.
(2) 求∠BAC的内角平分线所在直线方程.
(3)求AB边上的高所在的直线方程.解:(1)∠B是直线BA到BC的角(2)设P(x,y)为∠BAC的内角平分线所在直线上任意一点解得7x-7y+5=0或x+y+15=0由图形知7x-7y+5=0为所求(3)设AB边上的高所在的直线方程为3x-4y-5+λ(y-2)=0即3x-(4- λ)y-(5+2 λ)=0由直线垂直的充要条件,得解得λ=8所以所求直线方程是3x+4y-21=0例5. 正方形的中心为(-6,3),它的一边所在直线方程为5x+12y+7=0,求其它边所在直线方程。解:设正方形ABCD的边AB的方程是5x+12y+7=0∵CD∥AB ,∴CD边所在直线方程设为5x+12y+m=0(m≠7)∵正方形的中心P(-6,3)到直线5x+12y+7=0的距离d∴正方形的中心P到直线CD的距离是1∴直线CD的方程是5x+12y-19=0又AD、CB与直线AB垂直,可设AD、BC的方程是12x-5y+n=0∴AD、BC的方程是12x-5y+100=0或12x-5y+74=0例6.求直线a:2x+y-4=0关于直线L:3x+4y-1=0对称的直线b的方程分析:由平面几何知识,若直线a、b关于直线L对称,它们有下列几何性质:①若a、b相交,则L是a、b交角的平分线。②若点A在直线a上,那么,点A关于直线L的对称点B一定在直线b上,这时AB⊥L,且AB中点D在L上。解:解得a与L的交点E(3,-2),且点E在直线b上解法一:设直线b的斜率是k,又知a的斜率是-2,L的斜率是所以直线b的方程是即2x+11y+16=0求直线a:2x+y-4=0关于直线L:3x+4y-1=0对称的直线b的方程解法二:在直线a上取一点A(2,0),设点A关于直线L的对称点B的坐标是(x0,y0)AB则直线AB的方程是即4x-3y-8=0解得AB和L的交点M的坐标由中点坐标公式所以直线b的方程是∴b的方程是2x+11y+16=0例7.已知直线l经过点P(2,3),且和两条平行直线:3x+4y+8=0,3x+4y-7=0 分别交于A、B两点,且|AB|= 求直线l的方程分析 所求直线l经过点P(2,3),要想使问题解决,或求出它的斜率,或者再找到一个位于直线l上的点,此题难点是如何将条件|AB|= 转化为有用的信息
解:两条平行直线:3x+4y+8=0,3x+4y-7=0之间的距离因为|AB|=所以直线l与3x+4y+8=0的夹角是45o设直线l的斜率为k.则有即7x+y-17=0或x-7y+19=03x+4y+8=03x+4y-7=0BPA
