人教A版选择性必修第一册 1-4-1空间中点、直线和平面的向量表示 课件( 共24张PPT)
文档属性
| 名称 | 人教A版选择性必修第一册 1-4-1空间中点、直线和平面的向量表示 课件( 共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 940.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 16:24:57 | ||
图片预览







文档简介
(共24张PPT)
1.4.1空间中点、直线和平面的向量表示
空间向量与立体几何
第一课时
课程标准
理解利用向量表示空间中点、直线、平面的方式
掌握求取直线方向向量与平面法向量的方法
一
二
三
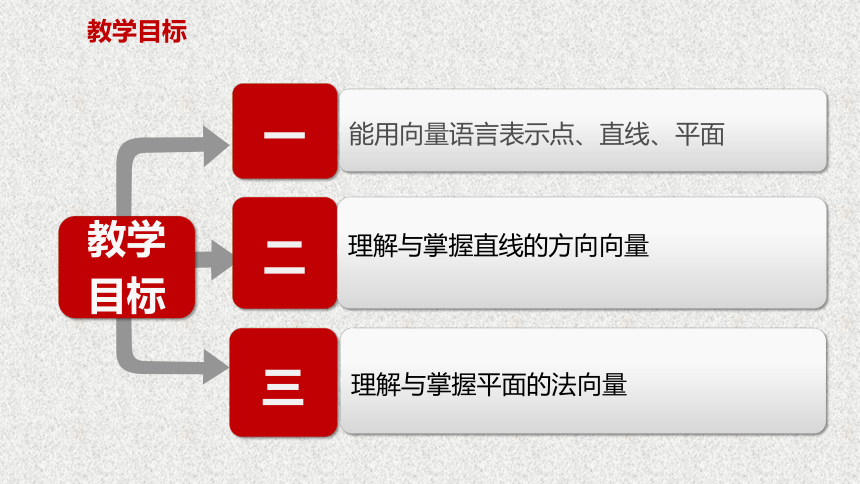
教学目标
能用向量语言表示点、直线、平面
理解与掌握直线的方向向量
理解与掌握平面的法向量
教学目标
重难点、易错点
重点
理解与掌握直线的方向向量、平面的法向量
难点
能用向量语言表示点、直线、平面
易错点
理解与掌握求平面的法向量的方法
复习回顾
我们上节课学习了什么知识呢?
1.空间向量运算的坐标表示
2.空间向量中平行、垂直的向量坐标之间的关系.
3.空间中两点间的距离公式和空间两向量夹角余弦值的计算公式.
(1)建系
(2)标点
(3)求向量
(4)算值(代公式)
方法:
新课导入
导
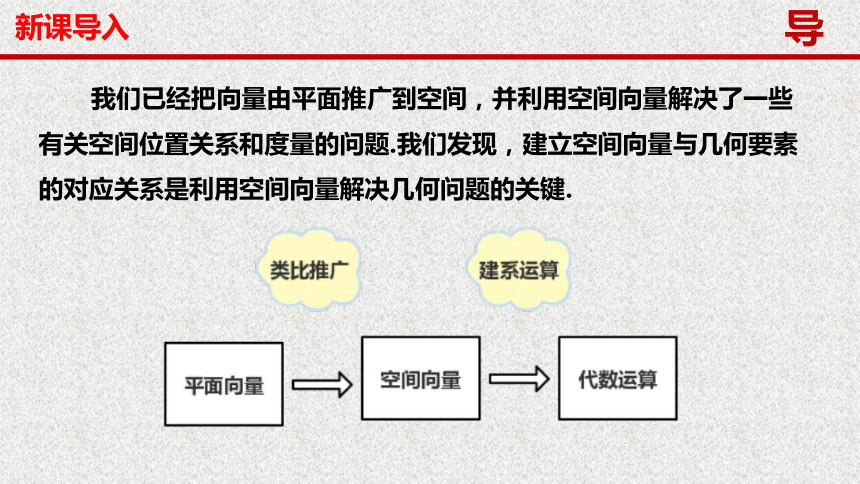
我们已经把向量由平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决几何问题的关键.
思
问题1 空间向量解决立体几何中那些问题?
可以解决立体几何中:
问题2 利用空间向量解决立体几何问题的关键是什么?
空间向量
立体几何
对应关系
点
线
面
思
探究一:用空间向量表示空间中点、线、面
思
问题4 如何用向量表示一个点?
如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示.我们把向量称为点P的位置向量.
O
P
定原点(参照物)
概念生成
思
问题5 如何用空间向量表示空间中的直线?
a
l
A
B
P
空间中给定一个点A和一个方向就能唯一确定一条直线l
几何中
一个点
一个方向
+
向量中
点
方向向量
如图,是直线l的方向向量,在直线l上取= ,设P是直线l上的任意一点,由向量共线的条件可知:
点P在直线l上充要条件存在实数t,使得,即
(1)= 为方向向量
(2)A,B,P三点共线
除了表示直线l,还有其他方法表示吗?
(A,B,P三点共线,还有其他表示方法吗?)
思
追问除了表示直线l,还有其他方法表示吗?
(1)= 为方向向量
(2)A,B,P三点共线(三角形法则)
空间直线的向量表示式
三角形法则
概念生成
空间直线的向量表示式
=
方向向量
空间任意直线由直线上一点和直线的方向向量唯一确定.
思
问题6 如何用空间向量表示平面?
(1)不共线的三点确定一个平面
(2)直线和直线外一点确定一个平面
(3)两条相交直线确定一个平面
(4)两条平行直线确定一个平面
立体几何
空间向量
?
在直线中:由直线上一点和直线的方向向量唯一确定.
一个定点和两个方向向量确定一个平面?
思
O
α
P
追问1 一个定点和两个方向向量确定一个平面?
共面向量定理:如果两个向量,不共线,那么向量与向量,共面的充要条件是存在唯一的有序实数对(x,y),使=x+y
OP=xa+yb
点O与向量,不仅可以确定平面α,还可以具体表示出面α内的任意一点.
这种表示在解决几何问题时有重要作用.
概念生成
α
A
C
P
O
如图,取定空间任意一点O,空间一点P位于平面ABC内的充要条件是存在实数x,y,使OP=OA+xAB+yAC.(三角形法则)
进一步:
我们把上式称为空间平面ABC的向量表示式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
空间中一点和一个向量是否可以表示一个平面?
问题7 空间中一点与一个方向向量如何表示一个平面?
给定空间一点A和一条直线l
过点A且垂直于直线l的平面是唯一确定的
利用点A和直线l的方向向量来确定平面.
思
概念生成
如图,直线l.取直线l的方向向量,我们称向量为平面α的法向量. 给定一个点A和一个向量,那么过点A,且以向量为法向量的平面完全确定,可以表示为集合{P|·=0}.
为面的法向量
共线
如果另有一条直线m面α,在直线m 上任取向量,与有什么关系
一个平面的法向量有无数条,他们之间的关系是共线的
概念生成
空间向量表示形式
点
直线
平面 1.点+两个不共线向量
2.点+平面法向量
=
为方向向量
OP=xa+yb
{P|
=0}
思
探究二:如何求直线的方向向量与求平面的法向量?
议、展、评
合作探究
如图,在长方体ABCD -A1B1C1D1,中,AB=4,BC=3,CC1=2,M是AB的中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求直线的方向向量
(2)求平面BCC1B1的法向量;
(3)求平面MCA1的法向量.
要求:(1)写出详细的解题步骤
(2)概括写题的方法
x
y
z
A1
D1
C1
B1
A
C
B
O
M
x
y
z
A1
D1
C1
B1
A
C
B
O
M
解:(1)因为AB=4,BC=3,CC1=2,M是AB的中点,所以M,A1的坐标分别为(3,2,0),(3,0,2).因此=(0,-2,2)
直线的方向向量为=(0,-2,2)
(2)因为y轴垂直于平面BCC1B,所以=(0,1,0)是平面 BCC1B1的一个法向量.
(1)去两点
(2)算向量
x
y
z
A1
D1
C1
B1
A
C
B
O
M
(3)因为AB=4,BC=3,CC1=2,M是AB的中点,所以M,C,A1的坐标分别为(3,2,0),(0,4,0),(3,0,2).因此(-3,2,0),=(0,-2,2).
设=(x,y,z)是平面MCA1的法向量,
则,
所以,
所以,
取z=3,则x=2,y=3.
于是=(2,3,3)是平面MCA1的一个法向量.
(1)算点,设法
(2)取向量:面内两个不共线向量
(3)建方程组
(4)取解
方法总结
(1)建系
(2)算点
(3)取向量
(4)建方程组
(5)取解
几何直观
运算
逻辑
直线的方向向量
法向量的运算
小结
1、空间中点、直线和平面的向量表示
点→点+位置向量
线→点+方向向量
平面→点+法向量
2.求直线的方向向量
3.求平面的方向向量
1.4.1空间中点、直线和平面的向量表示
空间向量与立体几何
第一课时
课程标准
理解利用向量表示空间中点、直线、平面的方式
掌握求取直线方向向量与平面法向量的方法
一
二
三
教学目标
能用向量语言表示点、直线、平面
理解与掌握直线的方向向量
理解与掌握平面的法向量
教学目标
重难点、易错点
重点
理解与掌握直线的方向向量、平面的法向量
难点
能用向量语言表示点、直线、平面
易错点
理解与掌握求平面的法向量的方法
复习回顾
我们上节课学习了什么知识呢?
1.空间向量运算的坐标表示
2.空间向量中平行、垂直的向量坐标之间的关系.
3.空间中两点间的距离公式和空间两向量夹角余弦值的计算公式.
(1)建系
(2)标点
(3)求向量
(4)算值(代公式)
方法:
新课导入
导
我们已经把向量由平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决几何问题的关键.
思
问题1 空间向量解决立体几何中那些问题?
可以解决立体几何中:
问题2 利用空间向量解决立体几何问题的关键是什么?
空间向量
立体几何
对应关系
点
线
面
思
探究一:用空间向量表示空间中点、线、面
思
问题4 如何用向量表示一个点?
如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示.我们把向量称为点P的位置向量.
O
P
定原点(参照物)
概念生成
思
问题5 如何用空间向量表示空间中的直线?
a
l
A
B
P
空间中给定一个点A和一个方向就能唯一确定一条直线l
几何中
一个点
一个方向
+
向量中
点
方向向量
如图,是直线l的方向向量,在直线l上取= ,设P是直线l上的任意一点,由向量共线的条件可知:
点P在直线l上充要条件存在实数t,使得,即
(1)= 为方向向量
(2)A,B,P三点共线
除了表示直线l,还有其他方法表示吗?
(A,B,P三点共线,还有其他表示方法吗?)
思
追问除了表示直线l,还有其他方法表示吗?
(1)= 为方向向量
(2)A,B,P三点共线(三角形法则)
空间直线的向量表示式
三角形法则
概念生成
空间直线的向量表示式
=
方向向量
空间任意直线由直线上一点和直线的方向向量唯一确定.
思
问题6 如何用空间向量表示平面?
(1)不共线的三点确定一个平面
(2)直线和直线外一点确定一个平面
(3)两条相交直线确定一个平面
(4)两条平行直线确定一个平面
立体几何
空间向量
?
在直线中:由直线上一点和直线的方向向量唯一确定.
一个定点和两个方向向量确定一个平面?
思
O
α
P
追问1 一个定点和两个方向向量确定一个平面?
共面向量定理:如果两个向量,不共线,那么向量与向量,共面的充要条件是存在唯一的有序实数对(x,y),使=x+y
OP=xa+yb
点O与向量,不仅可以确定平面α,还可以具体表示出面α内的任意一点.
这种表示在解决几何问题时有重要作用.
概念生成
α
A
C
P
O
如图,取定空间任意一点O,空间一点P位于平面ABC内的充要条件是存在实数x,y,使OP=OA+xAB+yAC.(三角形法则)
进一步:
我们把上式称为空间平面ABC的向量表示式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
空间中一点和一个向量是否可以表示一个平面?
问题7 空间中一点与一个方向向量如何表示一个平面?
给定空间一点A和一条直线l
过点A且垂直于直线l的平面是唯一确定的
利用点A和直线l的方向向量来确定平面.
思
概念生成
如图,直线l.取直线l的方向向量,我们称向量为平面α的法向量. 给定一个点A和一个向量,那么过点A,且以向量为法向量的平面完全确定,可以表示为集合{P|·=0}.
为面的法向量
共线
如果另有一条直线m面α,在直线m 上任取向量,与有什么关系
一个平面的法向量有无数条,他们之间的关系是共线的
概念生成
空间向量表示形式
点
直线
平面 1.点+两个不共线向量
2.点+平面法向量
=
为方向向量
OP=xa+yb
{P|
=0}
思
探究二:如何求直线的方向向量与求平面的法向量?
议、展、评
合作探究
如图,在长方体ABCD -A1B1C1D1,中,AB=4,BC=3,CC1=2,M是AB的中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求直线的方向向量
(2)求平面BCC1B1的法向量;
(3)求平面MCA1的法向量.
要求:(1)写出详细的解题步骤
(2)概括写题的方法
x
y
z
A1
D1
C1
B1
A
C
B
O
M
x
y
z
A1
D1
C1
B1
A
C
B
O
M
解:(1)因为AB=4,BC=3,CC1=2,M是AB的中点,所以M,A1的坐标分别为(3,2,0),(3,0,2).因此=(0,-2,2)
直线的方向向量为=(0,-2,2)
(2)因为y轴垂直于平面BCC1B,所以=(0,1,0)是平面 BCC1B1的一个法向量.
(1)去两点
(2)算向量
x
y
z
A1
D1
C1
B1
A
C
B
O
M
(3)因为AB=4,BC=3,CC1=2,M是AB的中点,所以M,C,A1的坐标分别为(3,2,0),(0,4,0),(3,0,2).因此(-3,2,0),=(0,-2,2).
设=(x,y,z)是平面MCA1的法向量,
则,
所以,
所以,
取z=3,则x=2,y=3.
于是=(2,3,3)是平面MCA1的一个法向量.
(1)算点,设法
(2)取向量:面内两个不共线向量
(3)建方程组
(4)取解
方法总结
(1)建系
(2)算点
(3)取向量
(4)建方程组
(5)取解
几何直观
运算
逻辑
直线的方向向量
法向量的运算
小结
1、空间中点、直线和平面的向量表示
点→点+位置向量
线→点+方向向量
平面→点+法向量
2.求直线的方向向量
3.求平面的方向向量
