人教A版选择性必修第一册 2-1-2 两条直线平行和垂直的判定 课件( 共24张PPT)
文档属性
| 名称 | 人教A版选择性必修第一册 2-1-2 两条直线平行和垂直的判定 课件( 共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 16:10:46 | ||
图片预览








文档简介
(共24张PPT)
2.1.2 两条直线平行和垂直的判定
人教A版选择性必修一
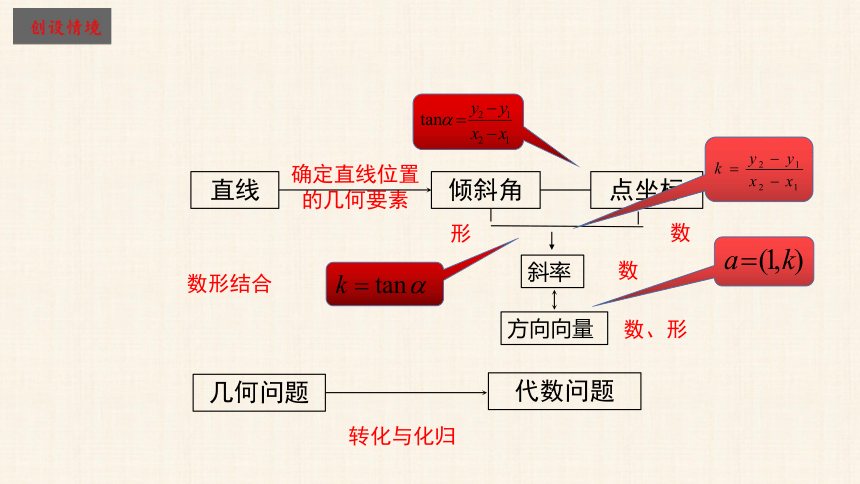
直线
倾斜角
确定直线位置
的几何要素
斜率
点坐标
方向向量
形
数
数
数、形
几何问题
代数问题
数形结合
转化与化归
问题1:平面中两条直线l1,l2有几种位置关系?
两种,相交和平行.
注:若今后没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.
学生探索
问题2:斜率是刻画直线倾斜程度的量,当两条直线相互平行或相互垂直时,它们之间的斜率有何关系?
学生探索
如图,直线l1与l2的倾斜角为α1,α2.
倾斜角的取值范围及正切函数的单调性
学生探索
于是,对于斜率分别为k1,k2的两条直线l1,l2有
存在
问题3:两条直线平行,它们的斜率一定相等吗?
学生探索
显然,当α1=α2=90°时,直线的斜率不存在,此时l1//l2.
学生探索
若直线l1,l2重合,此时仍然有k1=k2.
A,B,C三点共线
kAB=kAC
kAB=kBC
kAC=kBC
用斜率证明三点共线时,常常用到这个结论.
注:强调一下公共点
学生探索
例1 已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
分析:
绘图,猜想
思辨,论证
用代数方法研究几何问题
信息交流 运用规律
问题4:直线l1,l2垂直时,它们的斜
率除了不相等外,是否还有特殊
的数量关系?
平面内
两条直线
斜率相等
平行
相交
斜率不等
垂直
信息交流 运用规律
l1⊥l2 α2= α1+90o,
k2=tanα2=tan(α1+90o),
k1=tanα1.
思考:还有什么方法?
类比前面由倾斜角推导两条直线平行的方法,探究一下两条直线垂直的情况:
信息交流 运用规律
设两条直线l1,l2的斜率分别为k1,k2,则a=(1,k1),b=(1,k2)分别是直线l1,l2的一个方向向量.
信息交流 运用规律
当直线l1或l2的倾斜角为90°时,若l1⊥l2,则另一条直线的倾斜角为0°;反之亦然.
x
y
O
l1
l2
信息交流 运用规律
例2 已知A(5,-1),B(1,1),C(2,3)三点,
试判断△ABC的形状.
分析:如图,猜想AB⊥BC,
ABC是直角三角形.
变练演编
变式1:已知点A(5,–1),C(2,3) ,点B在x轴上,且∠ABC为直角,求点B的坐标.
分析:
设B(x,0)
计算kAB,kBC
kABkBC= 1
构造方程
变练演编
分析:
变式1:已知点A(5,–1),C(2,3) ,点B在x轴上,且∠ABC为直角,求点B的坐标.
综上,点B的坐标为 或 .
变练演编
类题通法
利用两条直线平行或垂直来判定图形形状的步骤
绘图
猜想
求斜率
结论
变练演编
变式2:已知A(5,-1),B(1,1),C(2,),若△ABC是直角三角形,试求 的值.
分类讨论的思想:讨论三种情况.
变练演编
解: 若∠A为直角,则AC⊥AB,∴kAC·kAB=-1,
若∠B为直角,则AB⊥BC,∴kAB·kBC=-1,
若∠C为直角,则AC⊥BC,∴kAC·kBC=-1,
综上所述,m=-7或m=3或m=±2.
变练演编
1.(多选)下列结论错误的是( )
A.若直线 的斜率相等,则
B.若直线 的斜率 ,则
C.若直线 的斜率都不存在,则
D.若直线 的斜率不相等,则 与 不平行
变练演编
:
2
1
l
l
和
解决1:对于两条不重合的直线
解决2:对于任意两条直线
:
2
1
l
l
和
l1∥l2 k1=k2
(条件:斜率都存在,且不重合)
或两直线中一个斜率不存在,一个斜率等于0
l1⊥l2 k1k2= –1(条件:斜率都存在)
或两直线斜率都不存在
反思小结
1
3
2
4
知识回顾
公式推导
绘图猜想
公式应用
数学抽象
数学运算
逻辑推理
直观想象
反思小结
几何问题
代数问题
代数问题的解
几何问题的解
直线方程
两直线交点
点到直线距离
······
数形结合
转化与化归
分类讨论
类比
反思小结
2.1.2 两条直线平行和垂直的判定
人教A版选择性必修一
直线
倾斜角
确定直线位置
的几何要素
斜率
点坐标
方向向量
形
数
数
数、形
几何问题
代数问题
数形结合
转化与化归
问题1:平面中两条直线l1,l2有几种位置关系?
两种,相交和平行.
注:若今后没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.
学生探索
问题2:斜率是刻画直线倾斜程度的量,当两条直线相互平行或相互垂直时,它们之间的斜率有何关系?
学生探索
如图,直线l1与l2的倾斜角为α1,α2.
倾斜角的取值范围及正切函数的单调性
学生探索
于是,对于斜率分别为k1,k2的两条直线l1,l2有
存在
问题3:两条直线平行,它们的斜率一定相等吗?
学生探索
显然,当α1=α2=90°时,直线的斜率不存在,此时l1//l2.
学生探索
若直线l1,l2重合,此时仍然有k1=k2.
A,B,C三点共线
kAB=kAC
kAB=kBC
kAC=kBC
用斜率证明三点共线时,常常用到这个结论.
注:强调一下公共点
学生探索
例1 已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
分析:
绘图,猜想
思辨,论证
用代数方法研究几何问题
信息交流 运用规律
问题4:直线l1,l2垂直时,它们的斜
率除了不相等外,是否还有特殊
的数量关系?
平面内
两条直线
斜率相等
平行
相交
斜率不等
垂直
信息交流 运用规律
l1⊥l2 α2= α1+90o,
k2=tanα2=tan(α1+90o),
k1=tanα1.
思考:还有什么方法?
类比前面由倾斜角推导两条直线平行的方法,探究一下两条直线垂直的情况:
信息交流 运用规律
设两条直线l1,l2的斜率分别为k1,k2,则a=(1,k1),b=(1,k2)分别是直线l1,l2的一个方向向量.
信息交流 运用规律
当直线l1或l2的倾斜角为90°时,若l1⊥l2,则另一条直线的倾斜角为0°;反之亦然.
x
y
O
l1
l2
信息交流 运用规律
例2 已知A(5,-1),B(1,1),C(2,3)三点,
试判断△ABC的形状.
分析:如图,猜想AB⊥BC,
ABC是直角三角形.
变练演编
变式1:已知点A(5,–1),C(2,3) ,点B在x轴上,且∠ABC为直角,求点B的坐标.
分析:
设B(x,0)
计算kAB,kBC
kABkBC= 1
构造方程
变练演编
分析:
变式1:已知点A(5,–1),C(2,3) ,点B在x轴上,且∠ABC为直角,求点B的坐标.
综上,点B的坐标为 或 .
变练演编
类题通法
利用两条直线平行或垂直来判定图形形状的步骤
绘图
猜想
求斜率
结论
变练演编
变式2:已知A(5,-1),B(1,1),C(2,),若△ABC是直角三角形,试求 的值.
分类讨论的思想:讨论三种情况.
变练演编
解: 若∠A为直角,则AC⊥AB,∴kAC·kAB=-1,
若∠B为直角,则AB⊥BC,∴kAB·kBC=-1,
若∠C为直角,则AC⊥BC,∴kAC·kBC=-1,
综上所述,m=-7或m=3或m=±2.
变练演编
1.(多选)下列结论错误的是( )
A.若直线 的斜率相等,则
B.若直线 的斜率 ,则
C.若直线 的斜率都不存在,则
D.若直线 的斜率不相等,则 与 不平行
变练演编
:
2
1
l
l
和
解决1:对于两条不重合的直线
解决2:对于任意两条直线
:
2
1
l
l
和
l1∥l2 k1=k2
(条件:斜率都存在,且不重合)
或两直线中一个斜率不存在,一个斜率等于0
l1⊥l2 k1k2= –1(条件:斜率都存在)
或两直线斜率都不存在
反思小结
1
3
2
4
知识回顾
公式推导
绘图猜想
公式应用
数学抽象
数学运算
逻辑推理
直观想象
反思小结
几何问题
代数问题
代数问题的解
几何问题的解
直线方程
两直线交点
点到直线距离
······
数形结合
转化与化归
分类讨论
类比
反思小结
