人教A版选择性必修第一册 2-2-2 直线的两点式方程 课件( 共17张PPT)
文档属性
| 名称 | 人教A版选择性必修第一册 2-2-2 直线的两点式方程 课件( 共17张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 856.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 00:00:00 | ||
图片预览







文档简介
(共17张PPT)
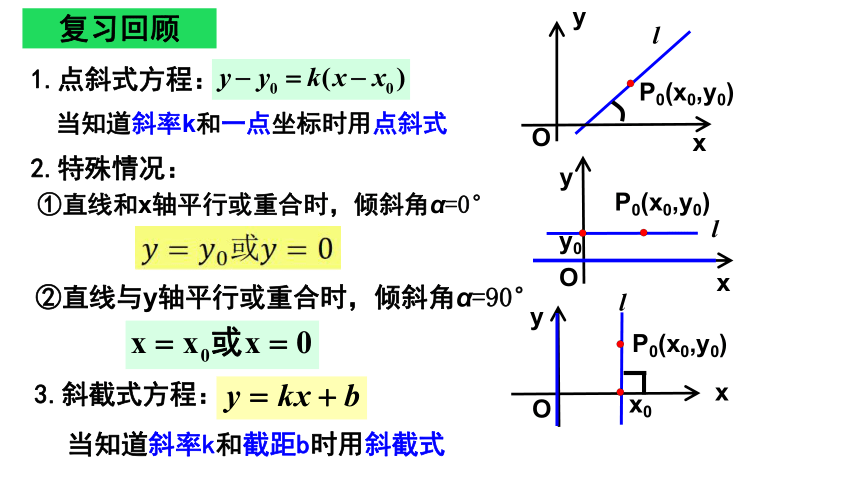
1.点斜式方程:
当知道斜率k和一点坐标时用点斜式
3.斜截式方程:
当知道斜率k和截距b时用斜截式
2.特殊情况:
①直线和x轴平行或重合时,倾斜角α=0°
②直线与y轴平行或重合时,倾斜角α=90°
复习回顾
x
y
l
O
P0(x0,y0)
x
y
l
y0
P0(x0,y0)
O
l
x
y
O
x0
P0(x0,y0)
第二章 直线和圆的方程
2.2 直线的方程
课时2 直线的两点式方程
1.掌握直线方程两点式的形式、特点及适用范围.(直观想象)
2.了解直线方程截距式的形式、特点及适用范围.(逻辑推理)
3.会用中点坐标公式求两点的中点坐标.(数学运算)
学习目标
x
y
l
P2(x2, y2)
P1(x1, y1)
O
知识点一 直线的两点式方程
注意:
(1)适用于斜率存在和斜率不等于0的直线,即与两坐标轴不垂直的直线.
(2)两点式方程与这两个点的顺序无关.
公式结构特点:(1)左边均为纵坐标y,右边均为横坐标x
(2)上下、左右下标序号一致
(3)方程中等号两边表达式中分子之比等于分母之比,也就是同一条直线的斜率相等.
笔记
思考
在P1(x1,y1),P2(x2,y2)中,如果x1=x2或y1=y2,则直线P1P2有没有两点式方程?方程分别为?
当x1=x2时,直线P1P2垂直于x轴,直线方程为:x=x1
当y1=y2时,直线P1P2垂直于y轴,直线方程为:y=y1
O
x
y
x1
O
x
y
y1
2.若点在过点,的直线上,则______.
1.过点和的直线方程是(@20@).
A.B.C.D.
B
导P68
-2
例3:已知直线l 与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程.
x
l
B(0,b)
A(a,0)
O
解:将两点A(a,0),B(0,b)的坐标代入两点式,得
即
y
横截距
纵截距
直线的截距式方程
知识点二 直线的截距式方程
书P63
x
l
B(0,b)
A(a,0)
O
*(1)截距式适用于横、纵截距都存在且都不为0的直线. 即过原点或与坐标轴平行的直线不能用截距式.
说明:
总结
我们把直线l与轴的交点(,0)的横坐标叫做直线在轴上的截距,
此时直线在y轴上的截距是b.
方程由直线l在两条坐标轴上的截距与b确定,我们把方程叫做直线的截距式方程,简称截距式.
(2)截距式方程是两点式方程的特殊情况,,所以截距式在解决直线与坐标轴围成的三角形的面积和周长问题时非常方便.
笔记
小组讨论
例2求过点
导P69
2min
提示:1.用截距式方程 2.截距可正,可负,可为0
总结:1.若直线l在两坐标轴上的截距相等,则直线l 的方程:
x+y=a
或y=kx
2.若直线l在两坐标轴上的截距互为相反数,则直线l的方程:
x-y=a
或y=kx
3.若直线l在两坐标轴上的截距绝对值相等,则直线l的方程:
x+y=a
或y=kx
或x-y=a
(1)若问题中涉及直线与两坐标轴相交,则可考虑选用直线的截距式方程,用待定系数法确定其系数即可.
(2)选用直线的截距式方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.
笔记
思考:截距式与两点式有什么联系和区别?
两点式:已知直线上两点的坐标,写出的直线方程.
截距式:已知直线在两个坐标轴上的截距, 写出的直线方程。
截距式方程是两点式方程
的特殊情况。
要求条件:斜率存在且斜率不为0的直线
要求条件:斜率存在且斜率不为0,还得不过原点的直线.
区别
联系
名 称 几 何 条 件 方程
直线方程的四种形式:
局限性
课堂小结
不垂直于x轴和y轴
不垂直于x轴
不垂直于x轴
x
y
P1(x1,y1)
P2(x2,y2)
M(x,y)
若点P1,P2的坐标分别为(x1,y1),(x2,y2),且线段P1P2的中点M的坐标为(x,y),则
x2
x
x1
y2
y
y2
知识点三 中点坐标公式
例4:三角形的顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线AM所在直线的方程.
x
y
O
C
B
A
.
.
.
.
M
解:过B(3,-3),C(0,2)两点式方程为
整理得:5x+3y-6=0
这就是BC边所在直线的方程。
书P63
边BC上的中线是顶点A与边BC中点M所连线段,由中点坐标公式,可得点M的坐标为,即.
过A(5,0),M两点的直线方程为:,
整理可得:x+13y+5=0.
这就是边 BC上中线AM所在直线的方程.
1.点斜式方程:
当知道斜率k和一点坐标时用点斜式
3.斜截式方程:
当知道斜率k和截距b时用斜截式
2.特殊情况:
①直线和x轴平行或重合时,倾斜角α=0°
②直线与y轴平行或重合时,倾斜角α=90°
复习回顾
x
y
l
O
P0(x0,y0)
x
y
l
y0
P0(x0,y0)
O
l
x
y
O
x0
P0(x0,y0)
第二章 直线和圆的方程
2.2 直线的方程
课时2 直线的两点式方程
1.掌握直线方程两点式的形式、特点及适用范围.(直观想象)
2.了解直线方程截距式的形式、特点及适用范围.(逻辑推理)
3.会用中点坐标公式求两点的中点坐标.(数学运算)
学习目标
x
y
l
P2(x2, y2)
P1(x1, y1)
O
知识点一 直线的两点式方程
注意:
(1)适用于斜率存在和斜率不等于0的直线,即与两坐标轴不垂直的直线.
(2)两点式方程与这两个点的顺序无关.
公式结构特点:(1)左边均为纵坐标y,右边均为横坐标x
(2)上下、左右下标序号一致
(3)方程中等号两边表达式中分子之比等于分母之比,也就是同一条直线的斜率相等.
笔记
思考
在P1(x1,y1),P2(x2,y2)中,如果x1=x2或y1=y2,则直线P1P2有没有两点式方程?方程分别为?
当x1=x2时,直线P1P2垂直于x轴,直线方程为:x=x1
当y1=y2时,直线P1P2垂直于y轴,直线方程为:y=y1
O
x
y
x1
O
x
y
y1
2.若点在过点,的直线上,则______.
1.过点和的直线方程是(@20@).
A.B.C.D.
B
导P68
-2
例3:已知直线l 与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程.
x
l
B(0,b)
A(a,0)
O
解:将两点A(a,0),B(0,b)的坐标代入两点式,得
即
y
横截距
纵截距
直线的截距式方程
知识点二 直线的截距式方程
书P63
x
l
B(0,b)
A(a,0)
O
*(1)截距式适用于横、纵截距都存在且都不为0的直线. 即过原点或与坐标轴平行的直线不能用截距式.
说明:
总结
我们把直线l与轴的交点(,0)的横坐标叫做直线在轴上的截距,
此时直线在y轴上的截距是b.
方程由直线l在两条坐标轴上的截距与b确定,我们把方程叫做直线的截距式方程,简称截距式.
(2)截距式方程是两点式方程的特殊情况,,所以截距式在解决直线与坐标轴围成的三角形的面积和周长问题时非常方便.
笔记
小组讨论
例2求过点
导P69
2min
提示:1.用截距式方程 2.截距可正,可负,可为0
总结:1.若直线l在两坐标轴上的截距相等,则直线l 的方程:
x+y=a
或y=kx
2.若直线l在两坐标轴上的截距互为相反数,则直线l的方程:
x-y=a
或y=kx
3.若直线l在两坐标轴上的截距绝对值相等,则直线l的方程:
x+y=a
或y=kx
或x-y=a
(1)若问题中涉及直线与两坐标轴相交,则可考虑选用直线的截距式方程,用待定系数法确定其系数即可.
(2)选用直线的截距式方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.
笔记
思考:截距式与两点式有什么联系和区别?
两点式:已知直线上两点的坐标,写出的直线方程.
截距式:已知直线在两个坐标轴上的截距, 写出的直线方程。
截距式方程是两点式方程
的特殊情况。
要求条件:斜率存在且斜率不为0的直线
要求条件:斜率存在且斜率不为0,还得不过原点的直线.
区别
联系
名 称 几 何 条 件 方程
直线方程的四种形式:
局限性
课堂小结
不垂直于x轴和y轴
不垂直于x轴
不垂直于x轴
x
y
P1(x1,y1)
P2(x2,y2)
M(x,y)
若点P1,P2的坐标分别为(x1,y1),(x2,y2),且线段P1P2的中点M的坐标为(x,y),则
x2
x
x1
y2
y
y2
知识点三 中点坐标公式
例4:三角形的顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线AM所在直线的方程.
x
y
O
C
B
A
.
.
.
.
M
解:过B(3,-3),C(0,2)两点式方程为
整理得:5x+3y-6=0
这就是BC边所在直线的方程。
书P63
边BC上的中线是顶点A与边BC中点M所连线段,由中点坐标公式,可得点M的坐标为,即.
过A(5,0),M两点的直线方程为:,
整理可得:x+13y+5=0.
这就是边 BC上中线AM所在直线的方程.
