【备考2023】湖北省武汉市中考数学模拟试卷1(含解析)
文档属性
| 名称 | 【备考2023】湖北省武汉市中考数学模拟试卷1(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 11:10:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【备考2023】湖北省武汉市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(共10小题,每小题3分,共30分。下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑)
1.如果a与互为相反数,那么a等于
A. B.3 C. D.
2.下列事件是必然事件的是( )
A.太阳从东方升起 B.汽车累计行驶1万千米,从未出现故障
C.姚明在罚球线上投篮一次,投中 D.经过有交通信号灯的路口,遇到绿灯
3.下列选项中的图案既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.下列运算中正确的是( )
A. B.
C. D.
5.如图,一个透明的玻璃正方体表面嵌有一根黑色的铁丝.这根铁丝在正方体俯视图中的形状是( )
A. B. C. D.
6.在函数的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y3<y1<y2 C.y3<y2<y1 D.y2<y1<y3
7.在平面直角坐标系中,点,,的图象如图所示,则a的值可以是( )
A.2 B. C. D.0.1
8.现有5张卡片,其中3张卡片正面上的图案是“”,2张卡片正面上的图案是“”,它们除此之外完全相同.把这5张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案相同的概率是( )
A. B. C. D.
9.下列结论:①的底数是;②若有理数a,b互为相反数,那么;③把1.804精确到0.01约等于1.80;④;⑤式子的最大值是6,其中正确的个数有( )
A.3个 B.2个 C.5个 D.4个
10.如图,矩形中,,分别为,的中点,且,,则的长为( )
A. B. C.3 D.
二、填空题(共6小题,每小题3分,共18分。下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.)
11.计算:______.
12.个裁判员对某一体操运动员的打分数据是:、、、、、,则这组数据的众数是______.
13.如果 ,那么A=__,B=___;
14.在中,若,则的度数是________.
15.已知抛物线与抛物线的形状相同,顶点在直线上,且顶点到轴的距离为5,则此抛物线的解析式为_________.
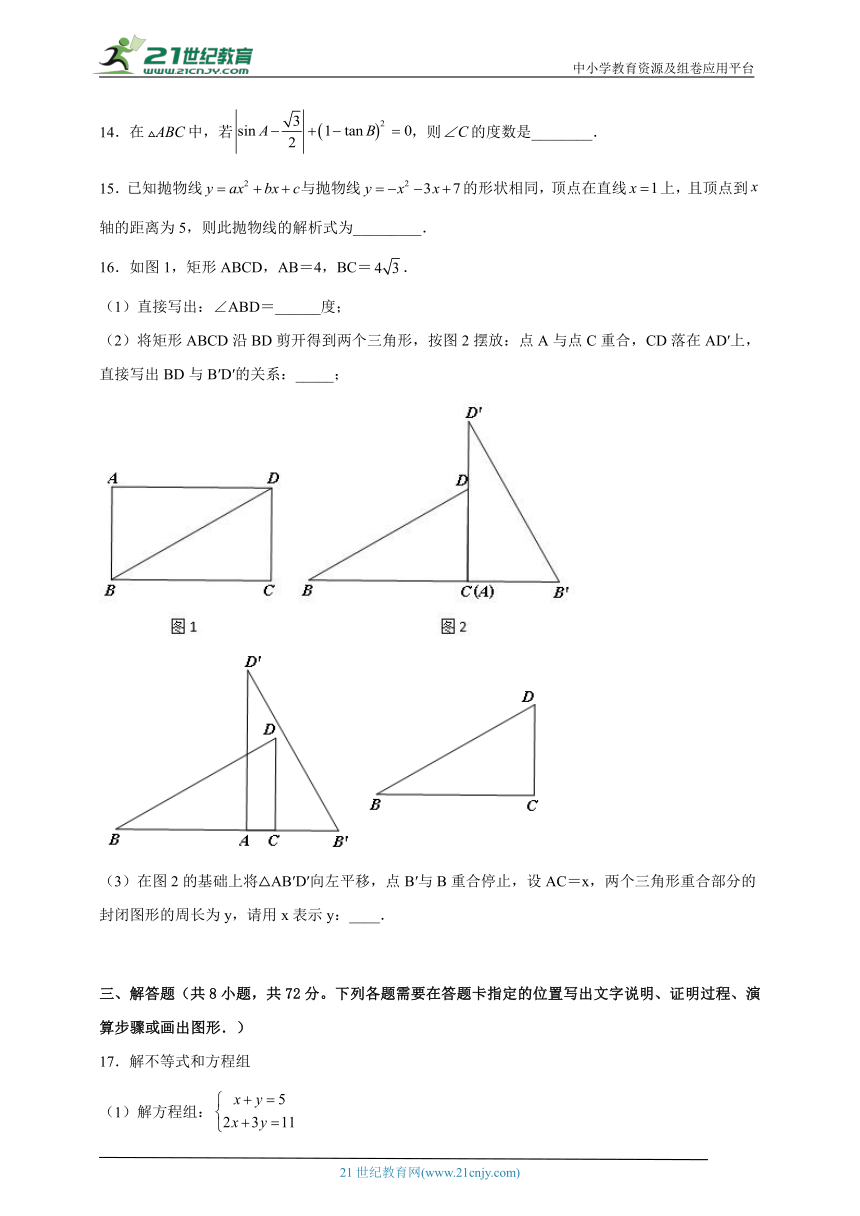
16.如图1,矩形ABCD,AB=4,BC=.
(1)直接写出:∠ABD=______度;
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
三、解答题(共8小题,共72分。下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.)
17.解不等式和方程组
(1)解方程组:
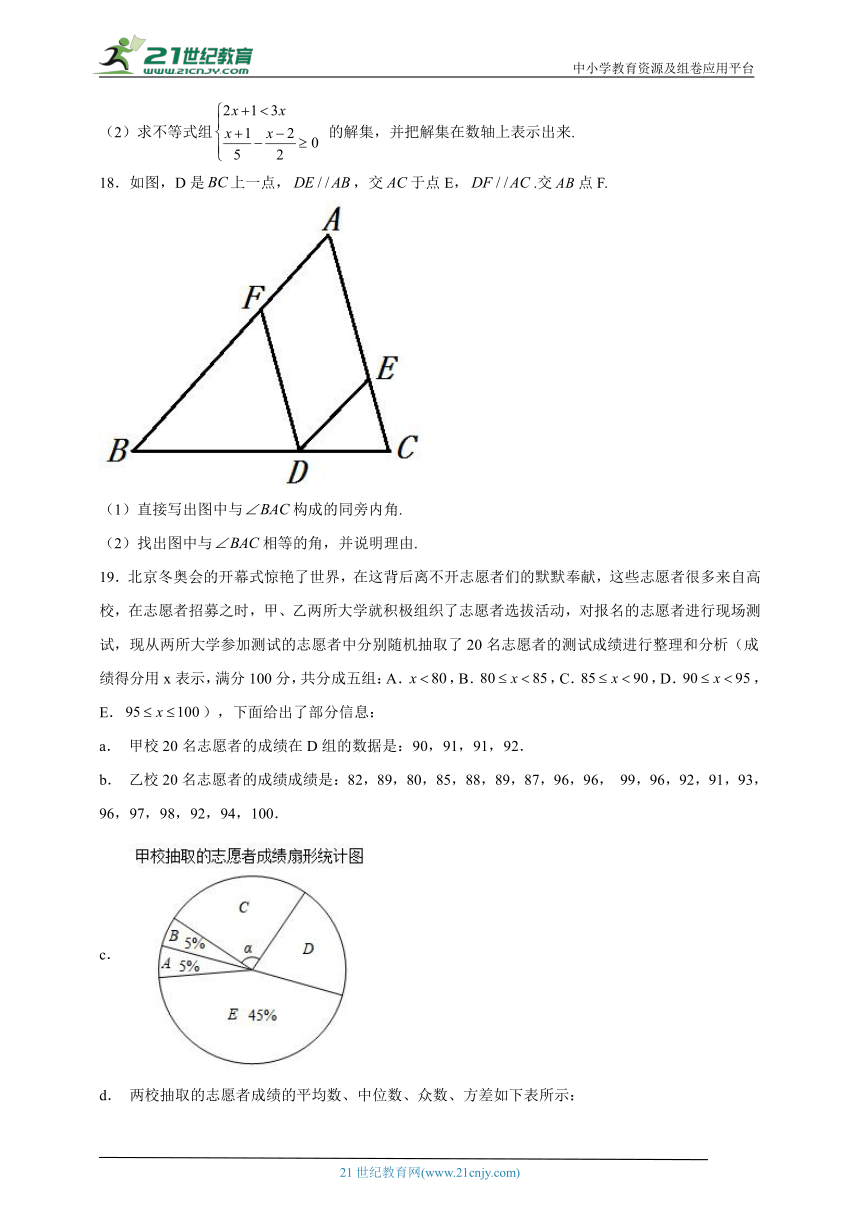
(2)求不等式组 的解集,并把解集在数轴上表示出来.
18.如图,D是上一点,,交于点E,.交点F.
(1)直接写出图中与构成的同旁内角.
(2)找出图中与相等的角,并说明理由.
19.北京冬奥会的开幕式惊艳了世界,在这背后离不开志愿者们的默默奉献,这些志愿者很多来自高校,在志愿者招募之时,甲、乙两所大学就积极组织了志愿者选拔活动,对报名的志愿者进行现场测试,现从两所大学参加测试的志愿者中分别随机抽取了20名志愿者的测试成绩进行整理和分析(成绩得分用x表示,满分100分,共分成五组:A.,B.,C.,D.,E.),下面给出了部分信息:
a. 甲校20名志愿者的成绩在D组的数据是:90,91,91,92.
b. 乙校20名志愿者的成绩成绩是:82,89,80,85,88,89,87,96,96, 99,96,92,91,93,96,97,98,92,94,100.
c.
d. 两校抽取的志愿者成绩的平均数、中位数、众数、方差如下表所示:
学校 平均数 中位数 众数 方差
甲 92 a 95 36.6
乙 92 92.5 b 31.4
根据以上信息,解答下列问题:
(1)由上表填空:a=___,b=___,= ___°.
(2)你认为哪个学校的志愿者测试成绩较好,请说明理由(写出一条即可).
(3)若甲校有200名志愿者,乙校有300名志愿者参加了此次侧试,估计此次参加测试的志愿者中,成绩在90分以上的志愿者有多少?
20.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.
求证:(1)BE⊥CE;
(2)BC=AB+CD.
21.如图,在由边长为1个单位长度的小正方形组成的8×8网格中,已知格点三角形ABC(顶点为网格线的交点).
(1)将△ABC绕点A顺时针旋转90°得到△AB1C1(点B,C的对应点分别为点B1,C1),画出△AB1C1;
(2)将△ABC平移,使得点A与点C1重合,得到△A2B2C2(点A,B,C的对应点分别为点A2,B2,C2,画出△A2B2C2)并说明平移过程;
(3)填空:sin∠B1C1B2=_______.
22.2022女足亚洲杯决赛中,中国女足时隔16年再次夺得亚洲杯冠军,向世界展示了中国精神和中国力量.某体育专卖店售卖各类体育用品,其中足球的进价为80元/个.经市场调查发现,在一段时间内,月销售量(个)与销售单价(元)()之间满足一次函数关系,当销售单价为100元时,月销售量为160个;当销售单价为110元时,月销售量为140个.
(1)求月销售量(个)与销售单价(元)之间的函数关系式;
(2)当销售单价定为90元时,该专卖店销售该足球的月利润为多少元?
23.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG的长.
24.抛物线 y=ax2 4ax+3a 交x轴于点B、C两点,交y轴于点A,点D为抛物线的顶点,连接AB、AC,已知△ABC的面积为3
(1)求抛物线的解析式;
(2)点P为抛物线对称轴右侧一点,点P的横坐标为m,过点P作PQ//AC交y轴于点Q,AQ的长度为d,求d与m的函数关系式;
(3)在(2)的条件下,当d=4时,作DN⊥y轴于点N,点G为抛物线上一点,AG交线段PD于点M,连接MN,若△AMN是以MN为底的等腰三角形,求点G的坐标.
参考答案:
1.【分析】根据相反数的性质即可解答.
解:由题意可得: ,解得 .
故选B.
【点评】本题主要考查相反数的性质(互为相反数的两个数相加等于0),熟记和掌握相反数的性质是解题关键.
2.【分析】根据确定事件和随机事件的定义来区分判断即可,必然事件和不可能事件统称确定性事件;必然事件:在一定条件下,一定会发生的事件称为必然事件;不可能事件:在一定条件下,一定不会发生的事件称为不可能事件;随机事件:在一定条件下,可能发生也可能不发生的事件称为随机事件.
解:A、太阳从东方升起,是必然事件,符合题意;
B、汽车累计行驶1万千米,从未出现故障,是随机事件,不符合题意;
C、姚明在罚球线上投篮一次,投中,是随机事件,不符合题意;
D、经过有交通信号灯的路口,遇到绿灯,是随机事件,不符合题意;
故选A.
【点评】本题考查了确定事件和随机事件的定义,熟悉定义是解题的关键.
3.【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
解:A、不是中心对称图形,不是轴对称图形,故此选项不合题意;
B、不是中心对称图形,是轴对称图形,故此选项不合题意;
C、不是中心对称图形,也不是轴对称图形,故此选项不合题意;
D、既是中心对称图形,也是轴对称图形,故此选项符合题意;
故选:D.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
4.【分析】利用合并同类项的法则进行计算,逐一判断即可解答.
解:A、与不能合并,故选项A不符合题意;
B、,故选项B符合题意;
C、,故选项C不符合题意;
D、与不能合并,故选项D不符合题意;
故选:B.
【点评】本题考查了合并同类项,熟练掌握合并同类项的法则是解题的关键.
5.【分析】根据从上面看得到的图形是俯视图,可得答案.
解:从上面看得到的图形是A表示的图形,
故选:A.
【点评】本题考查了组合体的三视图,从上面看得到的图形是俯视图.
6.【分析】根据反比例函数的性质可直接进行求解.
解:由可得:,
∴函数图像在第二、四象限,在每一象限内,y随x的增大而增大,
∵函数的图象上有三点(﹣3,y1),(-1,y2),(2,y3),
∴,
故选B.
【点评】本题主要考查反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
7.【分析】分析题中图形,可判断点,均在的图象的外面,即当时,抛物线上对应的函数值,当时,抛物线上对应的函数值,据此转化为解不等式组即可.
解:当时,
当时,
故选B
【点评】本题考查二次函数图象基本性质、点在坐标系中的坐标特征、点在图像外等知识,掌握采用数形结合方法解题是关键.
8.【分析】利用树状图列举出所有等可能的结果,再求两张卡片正面图案相同的概率.
解:令3张卡片正面上的图案是“”的为A1,A2,A3,2张卡片正面上的图案是“”的为B1,B2,画树状图如下:
所有机会均等的结果共20种,其中两张卡片正面图案相同的情况有8种
即两张卡片正面图案相同的概率P=
故选:B.
【点评】本题考查利用树状图或列表法求概率,是重要考点,掌握相关知识是解题关键.
9.【分析】根据乘方定义可判定①;根据相反数性质可计算得,从而可判定②;由近似数的精确度可求得近似数从而可判定③;根据合并同类项法则计算并判定④;根据绝对值的非负性可得式子的最小值是6,从而可判定⑤.
解:的底数是2,故①错误;
若有理数a,b互为相反数,那么,故②正确;
把1.804精确到0.01约等于1.80,故③正确;
化简合并同类项得0,故④正确;
式子的最小值是6,故⑤错误,
则其中正确的个数3个,
故选:A.
【点评】此题考查了整式的加减,以及绝对值的性质,近似数的求解,熟练掌握相关运算法则是解本题的关键.
10.【分析】根据矩形的性质可得 , , ,
从而,设 ,则 , ,可得,解出 ,最后在 中,利用勾股定理,即可解答.
解:在矩形中,,
∴ , , ,
∵,分别为,的中点,
∴ , ,
设 ,则 , ,
∵,
∴ ,
∴ ,
∵ ,
∴,
∴ ,
∴ ,
即 ,解得: 或(舍去),
∴ ,
在 中, .
故选:D
【点评】本题主要考查了矩形的性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握矩形的性质,找到相似三角形,根据相似三角形的对应边成比例解答即可.
11.【分析】利用二次根式的性质求解.
解:.
故答案为:3.
【点评】本题考查了二次根式的性质,熟记性质是解题的关键.
12.【分析】根据众数的定义求解即可.
解:这组数据中出现次数最多的数为,
即众数为.
故答案为:.
【点评】此题考查众数的定义,众数是这组数据中出现次数最多的数.
13.【分析】已知等式左边两项通分并利用同分母分式的加法法则计算,利用多项式相等的条件即可求出A与B的值.
解:,
可得(A+B)x+A-2B=3,
即A+B=0,A-2B=3,
解得:A=1,B=-1.
故答案为:1;-1.
【点评】本题考查了分式的加减法,分式加减法的关键是通分,通分的关键是找最简公分母.
14.【分析】根据非负性,求出,进而求出,根据三角形内角和,求出即可.
解:∵,,
∴,
∴,
∴,
∴;
故答案为:.
【点评】本题考查特殊角的三角函数值,非负性以及三角形的内角和.熟记特殊角的三角函数值,是解题的关键.
15.【分析】两个抛物线的形状相同,可知,则抛物线的解析式为;顶点在上,可以求出的值;又顶点到轴的距离是5,可以得到这个二次函数顶点纵坐标的绝对值是5,分情况讨论即可求出的值.
解:∵抛物线与抛物线的形状相同,
∴,
∴抛物线解析式为;,
∵抛物线顶点在直线上,
∴,
∴当时,,
∴;
当时,,
∴,
∴抛物线解析式为,或
,
∵抛物线顶点到轴的距离为5.
∴当
∴,解得或,
∴此时抛物线的解析式为:或;
∵当抛物线的解析式为时,
∴,解得或,
∴此时抛物线的解析式为:或.
∴抛物线的解析式为:或或或.
【点评】本题考查了二次函数的图像与几何变换,解答此题的关键是根据抛物线的对称轴方程得出抛物线的顶点式,然后求出的值,进而求出抛物线的解析式.
16.【分析】(1)解直角三角形即可解决问题.
(2)结论:BD⊥B′D′,BD=B′D′.利用“8字型”证明∠DHD′=∠BAD=90°即可.
(3)分四种情形①如图3-1中,当0<x≤时,重叠部分是四边形ACDH.②如图3-2中,当<x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当<x≤时,重叠部分是五边形ACMNH.如图3-4中,当<x<4+时,重叠部分是△BB′H.分别求解即可.
解:(1)如图1中,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=,
∴tan∠ABD=,
∴∠ABD=60°,
故答案为:60.
(2)结论:BD⊥B′D′,BD=B′D′.
理由:如图2中,延长BD交D′B′于H.
∵∠B=∠D′,∠BDA=∠HDD′,
∴∠BAD=∠DHD′=90°,
∴BD⊥B′D′.
∵BD与B′D′为矩形的对角线,则BD=B′D′;
故答案为:BD=B′D′,BD⊥B′D′.
(3)①如图3-1中,当0<x≤时,重叠部分是四边形ACDH,
由题意:AB=,AH=AB=,
∵AH∥CD,
∴,
∴,
∴BH=,
∴DH=8-()=,
y=x+4+
=x+4+4
=;
②如图3-2中,当<x≤4时,重叠部分是五边形ACMNH.
=
=;
③如图3-3中,当4<x≤时,重叠部分是四边形AB′NH.
=
=;
④如图3-4中,当时,重叠部分是△BB′H.
;
故答案为:;
【点评】本题属于四边形综合题,考查了平移变换,多边形的面积等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题,属于中考压轴题.
17.【分析】(1)利用加减消元法解二元一次方程组即可;
(2)根据一元一次不等式的性质求不等式组的解集,并再数轴上表示出来即可;
解: ①×3,得:=15 ③
③-②得x=4 ④
将④代入①解得y=1
方程组的解为:
(2) 解:<,解得>1
,解得≤4
∴不等式组的解集为1<x≤4
【点评】本题考查解二元一次方程组和解一元一次不等式组,熟练掌握解二元一次方程组和解一元一次不等式组是解题关键.
18.【分析】(1)根据同旁内角的概念解答即可;
(2)根据平行线的性质找到相等的角即可.
解:(1)由图知∠BAC的同旁内角有:∠AFD,∠AED,∠C,∠B;
(2)∵DE∥AB,
∴∠BAC=∠DEC,∠BFD=∠FDE,
∵DF∥AC,
∴∠BAC=∠BFD,
∴∠BAC=∠DEC=∠BFD=∠FDE.
【点评】本题是对平行线性质的考查,熟练掌握同旁内角的定义及平行线的性质是解决本题的关键.
19.【分析】(1)根据中位数、众数的意义分别求出a、b、的值以及α的值;
(2)根据中位数、众数的大小比较得出结论;
(3)求出90分以上学生所占的百分比即可
解:(1)解:甲校EE组20×45%=9(人),则第101,11个数据分别为91,92,
则,
乙校:96出现4次最多,则b=96,
甲校C组:20 4 9 20×(5%+5%)=5,则,
故答案为:91.5,96,90;
(2)解:乙校志愿者较好.
理由如下:
∵甲、乙两校的平均数虽然相同,但是乙校的中位数、众数均比甲校的大;或甲校的方差为36.6,乙校的方差是31.4,而,
∴乙校的成绩较为稳定,
∴乙校志愿者测试成绩较好;
(3)解:根据题意得:(人),
答:成绩在90分以上的共有315人.
【点评】本题考查中位数、众数、平均数以及样本估计总体,掌握平均数、中位数、众数的计算方法是正确解答的前提.
20.【分析】(1)先根据同旁内角互补得到∠1+∠2+∠3+∠4=180°,再利用角平分线性质即可解答,
(2)在BC上取点F,使BF=BA,连接EF,证明△ABE≌△FBE(SAS),△CDE≌△CFE(AAS)即可解题.
解:证明:如图所示:
(1)∵BE、CE分别是∠ABC和∠BCD的平分线,
∴∠1=∠2,∠3=∠4,
又∵AB∥CD,
∴∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∴∠BEC=90°,
∴BE⊥CE.
(2)在BC上取点F,使BF=BA,连接EF.
在△ABE和△FBE中,
,
∴△ABE≌△FBE(SAS),
∴∠A=∠5.
∵AB∥CD,
∴∠A+∠D=180°,
∴∠5+∠D=180,
∵∠5+∠6=180°,
∴∠6=∠D,
在△CDE和△CFE中,
,
∴△CDE≌△CFE(AAS),
∴CF=CD.
∵BC=BF+CF,
∴BC=AB+CD,
【点评】本题考查了平行线的性质,全等三角形的判定和性质,(1)中利用平行线的性质是解题关键,(2)中作辅助线证明三角形全等是解题关键.
21.【分析】(1)根据旋转的性质画图即可;
(2)根据平移的性质画图,根据平移变化描述过程即可;
(3) 过点B2作B2D⊥B1C1于点D,求出B2D 、B2C1即可.
解:(1)△AB1C1如图(1)所示.
(2)△A2B2C2如图(1)所示.
平移过程:将△ABC先向上平移1个单位长度,再向右平移4个单位长度或先向右平移4个单位长度,再向上平移1个单位长度.
(3)
如图(2),过点B2作B2D⊥B1C1于点D.
由题意可得,B1B2=1,B2C1=,B1C1=,
∵=×1×1=××B2D,
∴B2D=,
∴sin∠B1C1B2=.
故答案为:
【点评】本题考查了网格内的图形变换和解直角三角形,解题关键是熟练运用相关性质画图,构造直角三角形求三角函数值.
22.【分析】(1)设月销售量(个)与销售单价(元)之间的函数关系式为,根据“当销售单价为100元时,月销售量为160个;当销售单价为110元时,月销售量为140个”可得方程组,解之即可求得结论;
(2)根据“销售利润=每件销售利润×销售数量”据此即可求解.
解:(1)设月销售量(个)与销售单价(元)之间的函数关系式为,
由题意,得:,
解得:,
∴月销售量(个)与销售单价(元)之间的函数关系式为,
(2)由题意得:
当销售单价定为90元时,
专卖店销售该足球的月利润为:(元),
答:销售单价定为90元时,该专卖店销售该足球的月利润为1800元.
【点评】本题考查一次函数的应用,解题的关键正确解读题意,找准各数量之间的关系,求得月销售量(个)与销售单价(元)之间的函数关系式.
23.【分析】(1)连接OB,证得∠DBO=90°,即可得到BD与⊙O相切;
(2)由等腰直角三角形的性质得到CF=BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF=BF,根据勾股定理得到EF的长,根据圆的面积公式即可得到结论;
(3)根据等腰直角三角形和角平分线的定义即可得到结论.
解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,∠EBF=90°,
∴∠C=∠DBC,EF为直径,
∴点O在EF上,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF(ASA),
∵BC=BF,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴EF=
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=(EF)2 π=π=π;
(3)如图3,连接AE
∵AB=BE,∠ABE=90°,
∴∠AEB=45°,
∵EA=EC,
∴∠C=22.5°,
∴∠H=∠BEG=∠CED=90°﹣22.5°=67.5°,
∵BH平分∠CBF,
∴∠EBG=∠HBF=45°,
∴∠BGE=∠BFH=67.5°,
∴BG=BE=1,BH=BF=1+,
∴HG=BH﹣BG=.
【点评】本题考查全等三角形的判定和性质,切线的判定,圆周角定理,勾股定理,线段的垂直平分线的性质,直角三角形斜边上的中线等于斜边的一半,等腰直角三角形的判定和性质,熟练掌握这些定理,能根据定理正确作辅助线和推理是解决本题的关键.
24.【分析】(1)y=ax2-4ax+3a交x轴于点B、C两点,交y轴于点A,则点B、C的坐标分别为:(1,0)、(3,0),点A(0,3a),△ABC的面积=AB×OA=×2×3a=3,即可求解;
(2)PQ平行线于AC直线,其表达式设为:y=-x+b,设点P(m,m2-4m+3)(m>2),将点P的坐标代入上式,即可求解;
(3)d=4时,点P(4,3),设点,直线PD的函数表达式为:y=2x-5①,直线AG的函数表达式为:②,联立①②并解得:,故点,AN=AM,即2,即可求解.
解:(1)交x轴于B、C两点,
令y=0,则
解得,
∴点B、C的坐标分别为:、,
交交y轴于点A,
令x=0,则y=3a,
∴点,
∵的面积,解得:,
∴抛物线的表达式为:;
(2)如图,设直线AC的解析式为:y=kx+b,
∵点,点
代入得,,
解得,,
∴直线的解析式为;
∵
∴设的表达式设为:,
∵ ,
∴抛物线的对称轴为直线x=2,
∵点P为抛物线对称轴右侧一点,点P的横坐标为m,
∴设点,
将点P的坐标代入并解得:,
∴,
∵A(0,3),
∴OA=3,
∴;
(3)当时,则,
解得:或(舍去),
∴点,
如图,
∵
∴点,
∵DN⊥y轴于点N,
∵点
设直线PD的解析式为
把点(4,3),(2,-1)代入得
解得,
∴直线的函数表达式为:①,
设点,
设直线的函数表达式为:
把A(0,3),代入得,
解得
∴直线的函数表达式为: ②,
联立①②并解得:,
故点,
点、点,
∵,
∴,解得:或4,
∴点或.
【点评】本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、等腰三角形的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2023】湖北省武汉市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(共10小题,每小题3分,共30分。下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑)
1.如果a与互为相反数,那么a等于
A. B.3 C. D.
2.下列事件是必然事件的是( )
A.太阳从东方升起 B.汽车累计行驶1万千米,从未出现故障
C.姚明在罚球线上投篮一次,投中 D.经过有交通信号灯的路口,遇到绿灯
3.下列选项中的图案既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.下列运算中正确的是( )
A. B.
C. D.
5.如图,一个透明的玻璃正方体表面嵌有一根黑色的铁丝.这根铁丝在正方体俯视图中的形状是( )
A. B. C. D.
6.在函数的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y3<y1<y2 C.y3<y2<y1 D.y2<y1<y3
7.在平面直角坐标系中,点,,的图象如图所示,则a的值可以是( )
A.2 B. C. D.0.1
8.现有5张卡片,其中3张卡片正面上的图案是“”,2张卡片正面上的图案是“”,它们除此之外完全相同.把这5张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案相同的概率是( )
A. B. C. D.
9.下列结论:①的底数是;②若有理数a,b互为相反数,那么;③把1.804精确到0.01约等于1.80;④;⑤式子的最大值是6,其中正确的个数有( )
A.3个 B.2个 C.5个 D.4个
10.如图,矩形中,,分别为,的中点,且,,则的长为( )
A. B. C.3 D.
二、填空题(共6小题,每小题3分,共18分。下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.)
11.计算:______.
12.个裁判员对某一体操运动员的打分数据是:、、、、、,则这组数据的众数是______.
13.如果 ,那么A=__,B=___;
14.在中,若,则的度数是________.
15.已知抛物线与抛物线的形状相同,顶点在直线上,且顶点到轴的距离为5,则此抛物线的解析式为_________.
16.如图1,矩形ABCD,AB=4,BC=.
(1)直接写出:∠ABD=______度;
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
三、解答题(共8小题,共72分。下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.)
17.解不等式和方程组
(1)解方程组:
(2)求不等式组 的解集,并把解集在数轴上表示出来.
18.如图,D是上一点,,交于点E,.交点F.
(1)直接写出图中与构成的同旁内角.
(2)找出图中与相等的角,并说明理由.
19.北京冬奥会的开幕式惊艳了世界,在这背后离不开志愿者们的默默奉献,这些志愿者很多来自高校,在志愿者招募之时,甲、乙两所大学就积极组织了志愿者选拔活动,对报名的志愿者进行现场测试,现从两所大学参加测试的志愿者中分别随机抽取了20名志愿者的测试成绩进行整理和分析(成绩得分用x表示,满分100分,共分成五组:A.,B.,C.,D.,E.),下面给出了部分信息:
a. 甲校20名志愿者的成绩在D组的数据是:90,91,91,92.
b. 乙校20名志愿者的成绩成绩是:82,89,80,85,88,89,87,96,96, 99,96,92,91,93,96,97,98,92,94,100.
c.
d. 两校抽取的志愿者成绩的平均数、中位数、众数、方差如下表所示:
学校 平均数 中位数 众数 方差
甲 92 a 95 36.6
乙 92 92.5 b 31.4
根据以上信息,解答下列问题:
(1)由上表填空:a=___,b=___,= ___°.
(2)你认为哪个学校的志愿者测试成绩较好,请说明理由(写出一条即可).
(3)若甲校有200名志愿者,乙校有300名志愿者参加了此次侧试,估计此次参加测试的志愿者中,成绩在90分以上的志愿者有多少?
20.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.
求证:(1)BE⊥CE;
(2)BC=AB+CD.
21.如图,在由边长为1个单位长度的小正方形组成的8×8网格中,已知格点三角形ABC(顶点为网格线的交点).
(1)将△ABC绕点A顺时针旋转90°得到△AB1C1(点B,C的对应点分别为点B1,C1),画出△AB1C1;
(2)将△ABC平移,使得点A与点C1重合,得到△A2B2C2(点A,B,C的对应点分别为点A2,B2,C2,画出△A2B2C2)并说明平移过程;
(3)填空:sin∠B1C1B2=_______.
22.2022女足亚洲杯决赛中,中国女足时隔16年再次夺得亚洲杯冠军,向世界展示了中国精神和中国力量.某体育专卖店售卖各类体育用品,其中足球的进价为80元/个.经市场调查发现,在一段时间内,月销售量(个)与销售单价(元)()之间满足一次函数关系,当销售单价为100元时,月销售量为160个;当销售单价为110元时,月销售量为140个.
(1)求月销售量(个)与销售单价(元)之间的函数关系式;
(2)当销售单价定为90元时,该专卖店销售该足球的月利润为多少元?
23.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG的长.
24.抛物线 y=ax2 4ax+3a 交x轴于点B、C两点,交y轴于点A,点D为抛物线的顶点,连接AB、AC,已知△ABC的面积为3
(1)求抛物线的解析式;
(2)点P为抛物线对称轴右侧一点,点P的横坐标为m,过点P作PQ//AC交y轴于点Q,AQ的长度为d,求d与m的函数关系式;
(3)在(2)的条件下,当d=4时,作DN⊥y轴于点N,点G为抛物线上一点,AG交线段PD于点M,连接MN,若△AMN是以MN为底的等腰三角形,求点G的坐标.
参考答案:
1.【分析】根据相反数的性质即可解答.
解:由题意可得: ,解得 .
故选B.
【点评】本题主要考查相反数的性质(互为相反数的两个数相加等于0),熟记和掌握相反数的性质是解题关键.
2.【分析】根据确定事件和随机事件的定义来区分判断即可,必然事件和不可能事件统称确定性事件;必然事件:在一定条件下,一定会发生的事件称为必然事件;不可能事件:在一定条件下,一定不会发生的事件称为不可能事件;随机事件:在一定条件下,可能发生也可能不发生的事件称为随机事件.
解:A、太阳从东方升起,是必然事件,符合题意;
B、汽车累计行驶1万千米,从未出现故障,是随机事件,不符合题意;
C、姚明在罚球线上投篮一次,投中,是随机事件,不符合题意;
D、经过有交通信号灯的路口,遇到绿灯,是随机事件,不符合题意;
故选A.
【点评】本题考查了确定事件和随机事件的定义,熟悉定义是解题的关键.
3.【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
解:A、不是中心对称图形,不是轴对称图形,故此选项不合题意;
B、不是中心对称图形,是轴对称图形,故此选项不合题意;
C、不是中心对称图形,也不是轴对称图形,故此选项不合题意;
D、既是中心对称图形,也是轴对称图形,故此选项符合题意;
故选:D.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
4.【分析】利用合并同类项的法则进行计算,逐一判断即可解答.
解:A、与不能合并,故选项A不符合题意;
B、,故选项B符合题意;
C、,故选项C不符合题意;
D、与不能合并,故选项D不符合题意;
故选:B.
【点评】本题考查了合并同类项,熟练掌握合并同类项的法则是解题的关键.
5.【分析】根据从上面看得到的图形是俯视图,可得答案.
解:从上面看得到的图形是A表示的图形,
故选:A.
【点评】本题考查了组合体的三视图,从上面看得到的图形是俯视图.
6.【分析】根据反比例函数的性质可直接进行求解.
解:由可得:,
∴函数图像在第二、四象限,在每一象限内,y随x的增大而增大,
∵函数的图象上有三点(﹣3,y1),(-1,y2),(2,y3),
∴,
故选B.
【点评】本题主要考查反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
7.【分析】分析题中图形,可判断点,均在的图象的外面,即当时,抛物线上对应的函数值,当时,抛物线上对应的函数值,据此转化为解不等式组即可.
解:当时,
当时,
故选B
【点评】本题考查二次函数图象基本性质、点在坐标系中的坐标特征、点在图像外等知识,掌握采用数形结合方法解题是关键.
8.【分析】利用树状图列举出所有等可能的结果,再求两张卡片正面图案相同的概率.
解:令3张卡片正面上的图案是“”的为A1,A2,A3,2张卡片正面上的图案是“”的为B1,B2,画树状图如下:
所有机会均等的结果共20种,其中两张卡片正面图案相同的情况有8种
即两张卡片正面图案相同的概率P=
故选:B.
【点评】本题考查利用树状图或列表法求概率,是重要考点,掌握相关知识是解题关键.
9.【分析】根据乘方定义可判定①;根据相反数性质可计算得,从而可判定②;由近似数的精确度可求得近似数从而可判定③;根据合并同类项法则计算并判定④;根据绝对值的非负性可得式子的最小值是6,从而可判定⑤.
解:的底数是2,故①错误;
若有理数a,b互为相反数,那么,故②正确;
把1.804精确到0.01约等于1.80,故③正确;
化简合并同类项得0,故④正确;
式子的最小值是6,故⑤错误,
则其中正确的个数3个,
故选:A.
【点评】此题考查了整式的加减,以及绝对值的性质,近似数的求解,熟练掌握相关运算法则是解本题的关键.
10.【分析】根据矩形的性质可得 , , ,
从而,设 ,则 , ,可得,解出 ,最后在 中,利用勾股定理,即可解答.
解:在矩形中,,
∴ , , ,
∵,分别为,的中点,
∴ , ,
设 ,则 , ,
∵,
∴ ,
∴ ,
∵ ,
∴,
∴ ,
∴ ,
即 ,解得: 或(舍去),
∴ ,
在 中, .
故选:D
【点评】本题主要考查了矩形的性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握矩形的性质,找到相似三角形,根据相似三角形的对应边成比例解答即可.
11.【分析】利用二次根式的性质求解.
解:.
故答案为:3.
【点评】本题考查了二次根式的性质,熟记性质是解题的关键.
12.【分析】根据众数的定义求解即可.
解:这组数据中出现次数最多的数为,
即众数为.
故答案为:.
【点评】此题考查众数的定义,众数是这组数据中出现次数最多的数.
13.【分析】已知等式左边两项通分并利用同分母分式的加法法则计算,利用多项式相等的条件即可求出A与B的值.
解:,
可得(A+B)x+A-2B=3,
即A+B=0,A-2B=3,
解得:A=1,B=-1.
故答案为:1;-1.
【点评】本题考查了分式的加减法,分式加减法的关键是通分,通分的关键是找最简公分母.
14.【分析】根据非负性,求出,进而求出,根据三角形内角和,求出即可.
解:∵,,
∴,
∴,
∴,
∴;
故答案为:.
【点评】本题考查特殊角的三角函数值,非负性以及三角形的内角和.熟记特殊角的三角函数值,是解题的关键.
15.【分析】两个抛物线的形状相同,可知,则抛物线的解析式为;顶点在上,可以求出的值;又顶点到轴的距离是5,可以得到这个二次函数顶点纵坐标的绝对值是5,分情况讨论即可求出的值.
解:∵抛物线与抛物线的形状相同,
∴,
∴抛物线解析式为;,
∵抛物线顶点在直线上,
∴,
∴当时,,
∴;
当时,,
∴,
∴抛物线解析式为,或
,
∵抛物线顶点到轴的距离为5.
∴当
∴,解得或,
∴此时抛物线的解析式为:或;
∵当抛物线的解析式为时,
∴,解得或,
∴此时抛物线的解析式为:或.
∴抛物线的解析式为:或或或.
【点评】本题考查了二次函数的图像与几何变换,解答此题的关键是根据抛物线的对称轴方程得出抛物线的顶点式,然后求出的值,进而求出抛物线的解析式.
16.【分析】(1)解直角三角形即可解决问题.
(2)结论:BD⊥B′D′,BD=B′D′.利用“8字型”证明∠DHD′=∠BAD=90°即可.
(3)分四种情形①如图3-1中,当0<x≤时,重叠部分是四边形ACDH.②如图3-2中,当<x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当<x≤时,重叠部分是五边形ACMNH.如图3-4中,当<x<4+时,重叠部分是△BB′H.分别求解即可.
解:(1)如图1中,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=,
∴tan∠ABD=,
∴∠ABD=60°,
故答案为:60.
(2)结论:BD⊥B′D′,BD=B′D′.
理由:如图2中,延长BD交D′B′于H.
∵∠B=∠D′,∠BDA=∠HDD′,
∴∠BAD=∠DHD′=90°,
∴BD⊥B′D′.
∵BD与B′D′为矩形的对角线,则BD=B′D′;
故答案为:BD=B′D′,BD⊥B′D′.
(3)①如图3-1中,当0<x≤时,重叠部分是四边形ACDH,
由题意:AB=,AH=AB=,
∵AH∥CD,
∴,
∴,
∴BH=,
∴DH=8-()=,
y=x+4+
=x+4+4
=;
②如图3-2中,当<x≤4时,重叠部分是五边形ACMNH.
=
=;
③如图3-3中,当4<x≤时,重叠部分是四边形AB′NH.
=
=;
④如图3-4中,当时,重叠部分是△BB′H.
;
故答案为:;
【点评】本题属于四边形综合题,考查了平移变换,多边形的面积等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题,属于中考压轴题.
17.【分析】(1)利用加减消元法解二元一次方程组即可;
(2)根据一元一次不等式的性质求不等式组的解集,并再数轴上表示出来即可;
解: ①×3,得:=15 ③
③-②得x=4 ④
将④代入①解得y=1
方程组的解为:
(2) 解:<,解得>1
,解得≤4
∴不等式组的解集为1<x≤4
【点评】本题考查解二元一次方程组和解一元一次不等式组,熟练掌握解二元一次方程组和解一元一次不等式组是解题关键.
18.【分析】(1)根据同旁内角的概念解答即可;
(2)根据平行线的性质找到相等的角即可.
解:(1)由图知∠BAC的同旁内角有:∠AFD,∠AED,∠C,∠B;
(2)∵DE∥AB,
∴∠BAC=∠DEC,∠BFD=∠FDE,
∵DF∥AC,
∴∠BAC=∠BFD,
∴∠BAC=∠DEC=∠BFD=∠FDE.
【点评】本题是对平行线性质的考查,熟练掌握同旁内角的定义及平行线的性质是解决本题的关键.
19.【分析】(1)根据中位数、众数的意义分别求出a、b、的值以及α的值;
(2)根据中位数、众数的大小比较得出结论;
(3)求出90分以上学生所占的百分比即可
解:(1)解:甲校EE组20×45%=9(人),则第101,11个数据分别为91,92,
则,
乙校:96出现4次最多,则b=96,
甲校C组:20 4 9 20×(5%+5%)=5,则,
故答案为:91.5,96,90;
(2)解:乙校志愿者较好.
理由如下:
∵甲、乙两校的平均数虽然相同,但是乙校的中位数、众数均比甲校的大;或甲校的方差为36.6,乙校的方差是31.4,而,
∴乙校的成绩较为稳定,
∴乙校志愿者测试成绩较好;
(3)解:根据题意得:(人),
答:成绩在90分以上的共有315人.
【点评】本题考查中位数、众数、平均数以及样本估计总体,掌握平均数、中位数、众数的计算方法是正确解答的前提.
20.【分析】(1)先根据同旁内角互补得到∠1+∠2+∠3+∠4=180°,再利用角平分线性质即可解答,
(2)在BC上取点F,使BF=BA,连接EF,证明△ABE≌△FBE(SAS),△CDE≌△CFE(AAS)即可解题.
解:证明:如图所示:
(1)∵BE、CE分别是∠ABC和∠BCD的平分线,
∴∠1=∠2,∠3=∠4,
又∵AB∥CD,
∴∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∴∠BEC=90°,
∴BE⊥CE.
(2)在BC上取点F,使BF=BA,连接EF.
在△ABE和△FBE中,
,
∴△ABE≌△FBE(SAS),
∴∠A=∠5.
∵AB∥CD,
∴∠A+∠D=180°,
∴∠5+∠D=180,
∵∠5+∠6=180°,
∴∠6=∠D,
在△CDE和△CFE中,
,
∴△CDE≌△CFE(AAS),
∴CF=CD.
∵BC=BF+CF,
∴BC=AB+CD,
【点评】本题考查了平行线的性质,全等三角形的判定和性质,(1)中利用平行线的性质是解题关键,(2)中作辅助线证明三角形全等是解题关键.
21.【分析】(1)根据旋转的性质画图即可;
(2)根据平移的性质画图,根据平移变化描述过程即可;
(3) 过点B2作B2D⊥B1C1于点D,求出B2D 、B2C1即可.
解:(1)△AB1C1如图(1)所示.
(2)△A2B2C2如图(1)所示.
平移过程:将△ABC先向上平移1个单位长度,再向右平移4个单位长度或先向右平移4个单位长度,再向上平移1个单位长度.
(3)
如图(2),过点B2作B2D⊥B1C1于点D.
由题意可得,B1B2=1,B2C1=,B1C1=,
∵=×1×1=××B2D,
∴B2D=,
∴sin∠B1C1B2=.
故答案为:
【点评】本题考查了网格内的图形变换和解直角三角形,解题关键是熟练运用相关性质画图,构造直角三角形求三角函数值.
22.【分析】(1)设月销售量(个)与销售单价(元)之间的函数关系式为,根据“当销售单价为100元时,月销售量为160个;当销售单价为110元时,月销售量为140个”可得方程组,解之即可求得结论;
(2)根据“销售利润=每件销售利润×销售数量”据此即可求解.
解:(1)设月销售量(个)与销售单价(元)之间的函数关系式为,
由题意,得:,
解得:,
∴月销售量(个)与销售单价(元)之间的函数关系式为,
(2)由题意得:
当销售单价定为90元时,
专卖店销售该足球的月利润为:(元),
答:销售单价定为90元时,该专卖店销售该足球的月利润为1800元.
【点评】本题考查一次函数的应用,解题的关键正确解读题意,找准各数量之间的关系,求得月销售量(个)与销售单价(元)之间的函数关系式.
23.【分析】(1)连接OB,证得∠DBO=90°,即可得到BD与⊙O相切;
(2)由等腰直角三角形的性质得到CF=BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF=BF,根据勾股定理得到EF的长,根据圆的面积公式即可得到结论;
(3)根据等腰直角三角形和角平分线的定义即可得到结论.
解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,∠EBF=90°,
∴∠C=∠DBC,EF为直径,
∴点O在EF上,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF(ASA),
∵BC=BF,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴EF=
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=(EF)2 π=π=π;
(3)如图3,连接AE
∵AB=BE,∠ABE=90°,
∴∠AEB=45°,
∵EA=EC,
∴∠C=22.5°,
∴∠H=∠BEG=∠CED=90°﹣22.5°=67.5°,
∵BH平分∠CBF,
∴∠EBG=∠HBF=45°,
∴∠BGE=∠BFH=67.5°,
∴BG=BE=1,BH=BF=1+,
∴HG=BH﹣BG=.
【点评】本题考查全等三角形的判定和性质,切线的判定,圆周角定理,勾股定理,线段的垂直平分线的性质,直角三角形斜边上的中线等于斜边的一半,等腰直角三角形的判定和性质,熟练掌握这些定理,能根据定理正确作辅助线和推理是解决本题的关键.
24.【分析】(1)y=ax2-4ax+3a交x轴于点B、C两点,交y轴于点A,则点B、C的坐标分别为:(1,0)、(3,0),点A(0,3a),△ABC的面积=AB×OA=×2×3a=3,即可求解;
(2)PQ平行线于AC直线,其表达式设为:y=-x+b,设点P(m,m2-4m+3)(m>2),将点P的坐标代入上式,即可求解;
(3)d=4时,点P(4,3),设点,直线PD的函数表达式为:y=2x-5①,直线AG的函数表达式为:②,联立①②并解得:,故点,AN=AM,即2,即可求解.
解:(1)交x轴于B、C两点,
令y=0,则
解得,
∴点B、C的坐标分别为:、,
交交y轴于点A,
令x=0,则y=3a,
∴点,
∵的面积,解得:,
∴抛物线的表达式为:;
(2)如图,设直线AC的解析式为:y=kx+b,
∵点,点
代入得,,
解得,,
∴直线的解析式为;
∵
∴设的表达式设为:,
∵ ,
∴抛物线的对称轴为直线x=2,
∵点P为抛物线对称轴右侧一点,点P的横坐标为m,
∴设点,
将点P的坐标代入并解得:,
∴,
∵A(0,3),
∴OA=3,
∴;
(3)当时,则,
解得:或(舍去),
∴点,
如图,
∵
∴点,
∵DN⊥y轴于点N,
∵点
设直线PD的解析式为
把点(4,3),(2,-1)代入得
解得,
∴直线的函数表达式为:①,
设点,
设直线的函数表达式为:
把A(0,3),代入得,
解得
∴直线的函数表达式为: ②,
联立①②并解得:,
故点,
点、点,
∵,
∴,解得:或4,
∴点或.
【点评】本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、等腰三角形的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
