28.1.2 正弦、余弦、正切函数的简单应用 教学设计 人教版九年级数学下册
文档属性
| 名称 | 28.1.2 正弦、余弦、正切函数的简单应用 教学设计 人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 137.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 21:43:08 | ||
图片预览

文档简介
《正弦、余弦、正切》教学设计
【教材分析】
本节课选自人教版九年级数学下册第二十八章《锐角三角函数》第一小节复习课,旨在学生熟练解决三角函数的一些问题,为后边解直角三角形奠定了基础.
【学情分析】
本节课前边已经学习了基本的正弦 余弦 正切的求法,他们已经能够熟练求一个角的三角函数值,对其解法已具有一定的分析解决能力,所以本节课只需老师引导,学生可自主完成.
【教学目标】
知识技能:正弦 余弦 正切的综合应用;使学生理解锐角三角函数间的关系.
过程与方法:逐步培养学生分析、比较、概括的思维能力,提高学生对几何图形的认识、感受三角函数的实际价值;
情感态度与价值观:让学生在探究中感受数学知识的实际应用价值,养成良好的学习习惯。
教学重点、难点
重点:锐角三角函数的概念及应用
难点:锐角三角函数的综合应用
【教学过程设计】
一、复习引入:
1.正弦 余弦 正切
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b
(1)正弦:(2)余弦:
(3)正切:
锐角三角函数:我们把∠A的正弦、余弦、
正切叫做∠A的锐角三角函数.
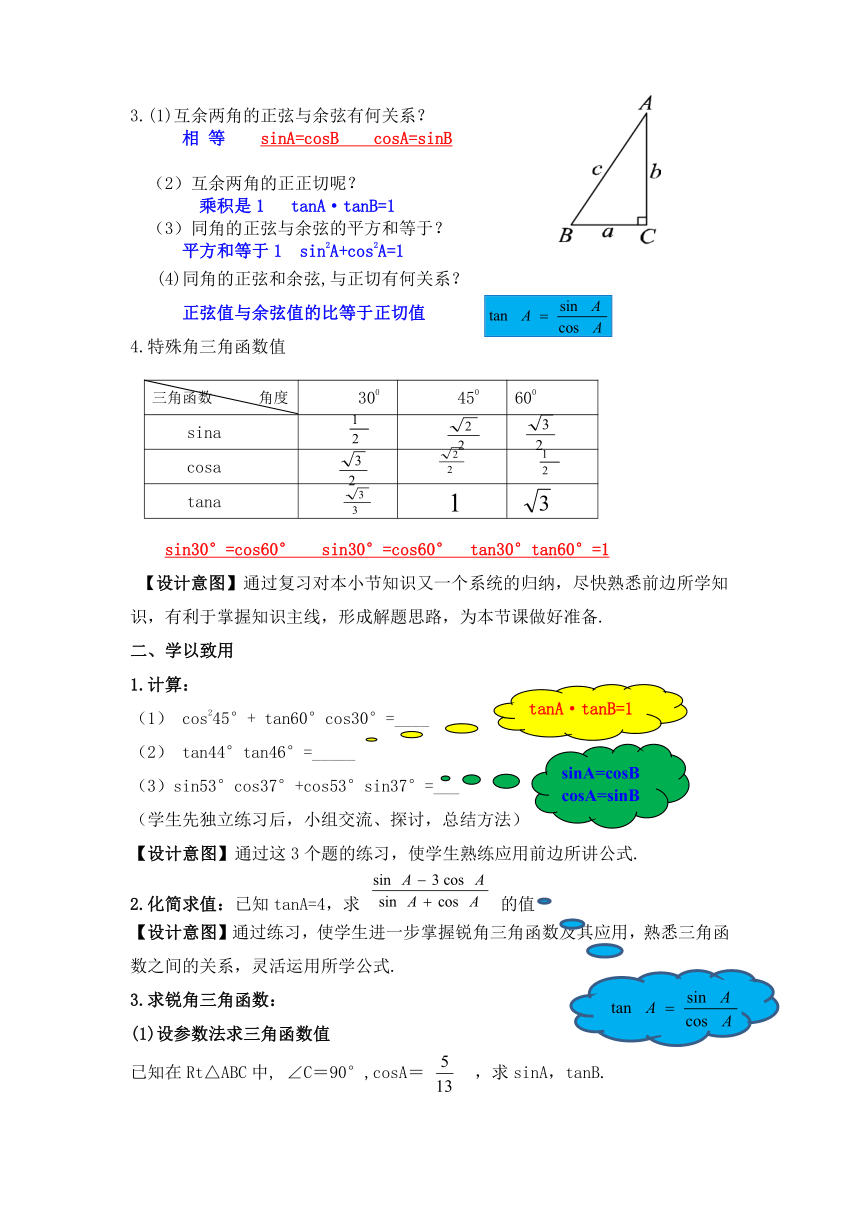
3.(1)互余两角的正弦与余弦有何关系?
相 等 sinA=cosB cosA=sinB
互余两角的正正切呢?
乘积是1 tanA·tanB=1
(3)同角的正弦与余弦的平方和等于?
平方和等于1 sin2A+cos2A=1
(4)同角的正弦和余弦,与正切有何关系?
正弦值与余弦值的比等于正切值
4.特殊角三角函数值
三角函数 角度 300 450 600
sina
cosa
tana
sin30°=cos60° sin30°=cos60° tan30°tan60°=1
【设计意图】通过复习对本小节知识又一个系统的归纳,尽快熟悉前边所学知识,有利于掌握知识主线,形成解题思路,为本节课做好准备.
二、学以致用
(
tanA·tanB=1
)1.计算:
(1) cos245°+ tan60°cos30°=____
(
sinA=cosB
cosA=sinB
)(2) tan44°tan46°=_____
(3)sin53°cos37°+cos53°sin37°=___
(学生先独立练习后,小组交流、探讨,总结方法)
【设计意图】通过这3个题的练习,使学生熟练应用前边所讲公式.
2.化简求值:已知tanA=4,求 的值
【设计意图】通过练习,使学生进一步掌握锐角三角函数及其应用,熟悉三角函数之间的关系,灵活运用所学公式.
3.求锐角三角函数:
(1)设参数法求三角函数值
已知在Rt△ABC中, ∠C=90°,cosA= ,求sinA,tanB.
【方法点拨】a.可先画出相应的直角三角形;
b.利用已知的三角函数值,通过采用设参数的方法,结合勾股定理表示出三角形的三条边的长;
c.根据锐角三角函数的定义求解.
(2)利用等角求三角函数值
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=____
解:连接BC,
∴∠D=∠A,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=3×2=6,AC=2,
【方法点拨】当不能直接锐角三角函数值时,可利用等角转换法,把要求的角转化为与其相等的角,找相等角有好多种方法:可以借助平行线、等腰三角形、三角形全等(相似)、圆等知识来解决,要根据题目的条件灵活选用方法。
(
A
C
B
)(3)构造直角三角形求三角函数值
在等腰△ABC中,AB=AC=13,BC=10.求sinB,cosB.
【方法点拨】锐角三角函数是在直角三角形的条件下定义的,因此当题目要求某一个锐角的三角函数值时,要先观察这个锐角是否在直角三角形中,如果不在,首先通过作辅助线,构造与该角有关的直角三角形,再利用锐角三角函数的定义求解。
【设计意图:通过专题模块训练,有利于学生对本小节知识归类,总结,进行条理、系统的复习,提高复习效率.】
三、快乐参与:
1.如图,折叠矩形ABCD的一边AD,使D落在BC边的点F处,已知AB=8cm, BC=10cm,求tan∠EAF的值.
2.在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。
【设计意图:让学生通过实践激发学生积极思考,认真交流;在学生小组讨论的过程中为学生提供充分从事数学活动的机会,从而激发学生的学习积极性,体会在解决问题的过程中,与他人合作的重要性】
五、课堂小结:
谈谈本节课你有哪些收获?
【设计意图:通过让学生自己总结学习的收获,使学生对锐角三角函数有系统的认识,体会三角函数之间的转化关系,目的是培养学生的归纳总结能力,锻炼他们的表达能力,通过自我评价,体现多元化的评价形式,培养学生的自信心.】
六、作业布置:
1.课本98页:第3,4题
111页:第2题
2.选做题:
【设计意图:分层作业中必作题体现新课标下落实“学有价值的数学”,达到“人人都能获得必需数学”;选做题让“不同的人在数学上得到不同的发展”,这样有利于学生的自主发展】
七、板书设计:
:
28.1正弦 余弦 正切
复习引入: 练习: 几个重要公式 例1: 例2: 例3
【教材分析】
本节课选自人教版九年级数学下册第二十八章《锐角三角函数》第一小节复习课,旨在学生熟练解决三角函数的一些问题,为后边解直角三角形奠定了基础.
【学情分析】
本节课前边已经学习了基本的正弦 余弦 正切的求法,他们已经能够熟练求一个角的三角函数值,对其解法已具有一定的分析解决能力,所以本节课只需老师引导,学生可自主完成.
【教学目标】
知识技能:正弦 余弦 正切的综合应用;使学生理解锐角三角函数间的关系.
过程与方法:逐步培养学生分析、比较、概括的思维能力,提高学生对几何图形的认识、感受三角函数的实际价值;
情感态度与价值观:让学生在探究中感受数学知识的实际应用价值,养成良好的学习习惯。
教学重点、难点
重点:锐角三角函数的概念及应用
难点:锐角三角函数的综合应用
【教学过程设计】
一、复习引入:
1.正弦 余弦 正切
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b
(1)正弦:(2)余弦:
(3)正切:
锐角三角函数:我们把∠A的正弦、余弦、
正切叫做∠A的锐角三角函数.
3.(1)互余两角的正弦与余弦有何关系?
相 等 sinA=cosB cosA=sinB
互余两角的正正切呢?
乘积是1 tanA·tanB=1
(3)同角的正弦与余弦的平方和等于?
平方和等于1 sin2A+cos2A=1
(4)同角的正弦和余弦,与正切有何关系?
正弦值与余弦值的比等于正切值
4.特殊角三角函数值
三角函数 角度 300 450 600
sina
cosa
tana
sin30°=cos60° sin30°=cos60° tan30°tan60°=1
【设计意图】通过复习对本小节知识又一个系统的归纳,尽快熟悉前边所学知识,有利于掌握知识主线,形成解题思路,为本节课做好准备.
二、学以致用
(
tanA·tanB=1
)1.计算:
(1) cos245°+ tan60°cos30°=____
(
sinA=cosB
cosA=sinB
)(2) tan44°tan46°=_____
(3)sin53°cos37°+cos53°sin37°=___
(学生先独立练习后,小组交流、探讨,总结方法)
【设计意图】通过这3个题的练习,使学生熟练应用前边所讲公式.
2.化简求值:已知tanA=4,求 的值
【设计意图】通过练习,使学生进一步掌握锐角三角函数及其应用,熟悉三角函数之间的关系,灵活运用所学公式.
3.求锐角三角函数:
(1)设参数法求三角函数值
已知在Rt△ABC中, ∠C=90°,cosA= ,求sinA,tanB.
【方法点拨】a.可先画出相应的直角三角形;
b.利用已知的三角函数值,通过采用设参数的方法,结合勾股定理表示出三角形的三条边的长;
c.根据锐角三角函数的定义求解.
(2)利用等角求三角函数值
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=____
解:连接BC,
∴∠D=∠A,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=3×2=6,AC=2,
【方法点拨】当不能直接锐角三角函数值时,可利用等角转换法,把要求的角转化为与其相等的角,找相等角有好多种方法:可以借助平行线、等腰三角形、三角形全等(相似)、圆等知识来解决,要根据题目的条件灵活选用方法。
(
A
C
B
)(3)构造直角三角形求三角函数值
在等腰△ABC中,AB=AC=13,BC=10.求sinB,cosB.
【方法点拨】锐角三角函数是在直角三角形的条件下定义的,因此当题目要求某一个锐角的三角函数值时,要先观察这个锐角是否在直角三角形中,如果不在,首先通过作辅助线,构造与该角有关的直角三角形,再利用锐角三角函数的定义求解。
【设计意图:通过专题模块训练,有利于学生对本小节知识归类,总结,进行条理、系统的复习,提高复习效率.】
三、快乐参与:
1.如图,折叠矩形ABCD的一边AD,使D落在BC边的点F处,已知AB=8cm, BC=10cm,求tan∠EAF的值.
2.在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。
【设计意图:让学生通过实践激发学生积极思考,认真交流;在学生小组讨论的过程中为学生提供充分从事数学活动的机会,从而激发学生的学习积极性,体会在解决问题的过程中,与他人合作的重要性】
五、课堂小结:
谈谈本节课你有哪些收获?
【设计意图:通过让学生自己总结学习的收获,使学生对锐角三角函数有系统的认识,体会三角函数之间的转化关系,目的是培养学生的归纳总结能力,锻炼他们的表达能力,通过自我评价,体现多元化的评价形式,培养学生的自信心.】
六、作业布置:
1.课本98页:第3,4题
111页:第2题
2.选做题:
【设计意图:分层作业中必作题体现新课标下落实“学有价值的数学”,达到“人人都能获得必需数学”;选做题让“不同的人在数学上得到不同的发展”,这样有利于学生的自主发展】
七、板书设计:
:
28.1正弦 余弦 正切
复习引入: 练习: 几个重要公式 例1: 例2: 例3
