第十四章整式的乘法与因式分解 (ab)n与杨辉三角教学设计(表格式)人教版八年级数学上册
文档属性
| 名称 | 第十四章整式的乘法与因式分解 (ab)n与杨辉三角教学设计(表格式)人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 21:51:23 | ||
图片预览

文档简介
教学设计
课题 (a+b)n与杨辉三角 课型 新授课 课时 1课时
年级 八年级 时间 节次 1
背景 分析 1.课程标准:通过教师在平时教学中渗透或通过课外阅读,了解杨辉三角的简史,掌握杨辉三角中隐含的基本规律,以拓宽整式乘法。 2.教材分析:本节是在学习了整式乘法的基础上进行探究的,是对整式乘法的拓展,为学习二项式(a+b)n 的展开式奠定基础,通过本节探究杨辉三角规律的教学,既能构建完整知识框架,又能多方位提高学生的数学素养。 3.学情分析: 本学段的学生具有对与自己的直观经验相冲突的现象和对有挑战性任务感兴趣的特点,也初步具备个体和群体参与“探究性问题”、“开放性问题”活动的能力,结合本节内容的特点,采用探究式学习方式,对于学生在探究过程中出现不全面、易出错等问题,教师给予及时的引导、点拨和激励评价。
学习 目标 1、了解(a+b)n(n=0,1,2,3……) 的展开式中的项数、项的次数、系数的规律。 2、探索并归纳展开式中的项数、项的次数、系数的一般规律。 3、了解 “杨辉三角”的历史。
评价 设计 1、采用课堂观察的方式进行评价。 2、采用随堂提问的方式进行评价。 3、采用达标检测的方式进行评价。
问题情境 师生活动 设计意图
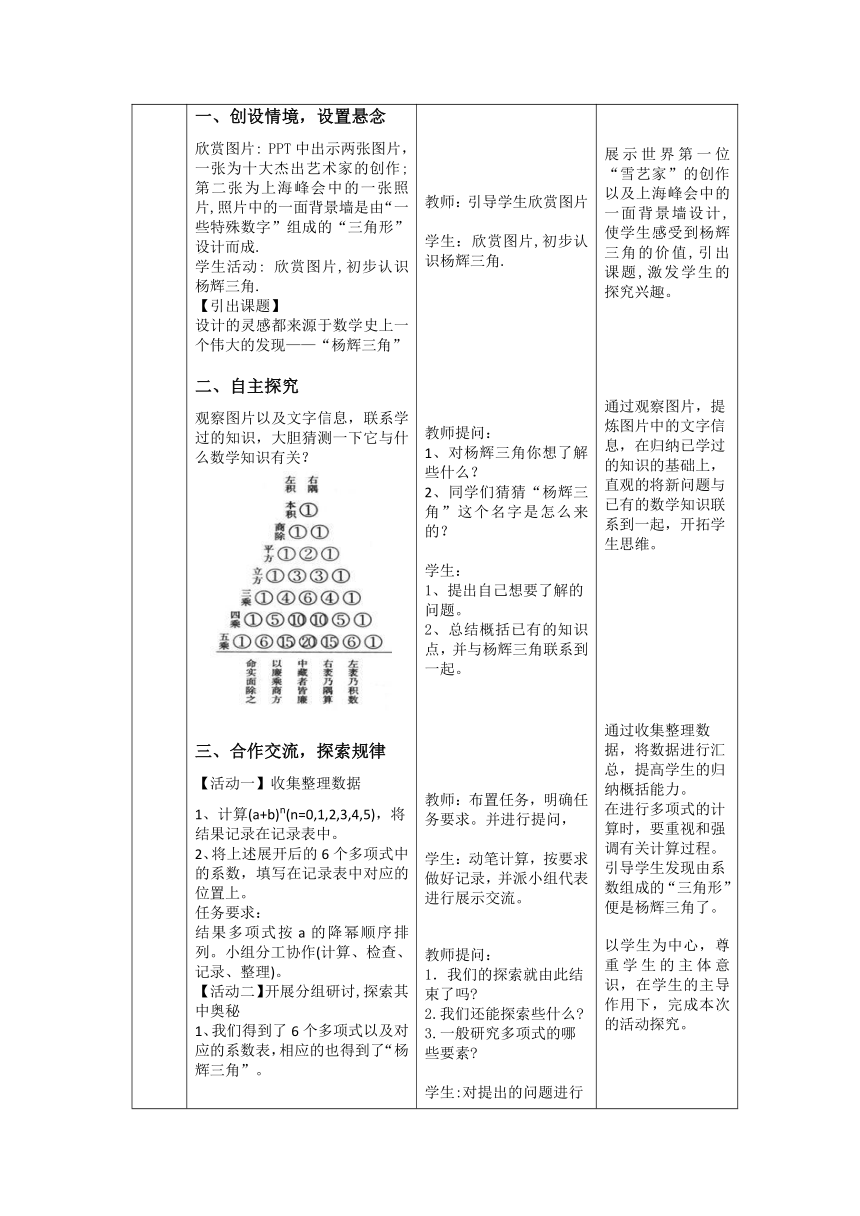
一、创设情境,设置悬念 欣赏图片: PPT中出示两张图片,一张为十大杰出艺术家的创作;第二张为上海峰会中的一张照片,照片中的一面背景墙是由“一些特殊数字”组成的“三角形”设计而成. 学生活动: 欣赏图片,初步认识杨辉三角. 【引出课题】 设计的灵感都来源于数学史上一个伟大的发现——“杨辉三角” 二、自主探究 观察图片以及文字信息,联系学过的知识,大胆猜测一下它与什么数学知识有关? 三、合作交流,探索规律 【活动一】收集整理数据 1、计算(a+b)n(n=0,1,2,3,4,5),将结果记录在记录表中。 2、将上述展开后的6个多项式中的系数,填写在记录表中对应的位置上。 任务要求: 结果多项式按a的降幂顺序排列。小组分工协作(计算、检查、记录、整理)。 【活动二】开展分组研讨,探索其中奥秘 1、我们得到了6个多项式以及对应的系数表,相应的也得到了“杨辉三角”。 2、【分组研讨】 【研讨问题1】观察得到的6个多项式,它们的项数有什么规律 【研讨问题2】每个多项式中,各项的次数有什么规律 【研讨问题3】观察系数表,你能发现哪些规律 【活动三】深入猜想验证,激发求知热情 【追问1】你能利用规律直接写出(a+b)7的展开式及系数吗 【追问2】当n=7,8,9,……时,我们怎么来验证呢 用已有的知识能验证“所有”吗 【总结】虽然可以用同样的方法逐一对更高次的情况进行验证,但是由于n可以取到无限大,所以用我们有限的知识和经验是无法完成的. 学无止境,当你学到的知识越来越多时,解决这个问题就是小菜一碟了.高中阶段我们就能深入探索这些规律了. 四、达标检测 1、将图补充完整。 2、直接写出〖( + )〗^5的展开式。 教师:引导学生欣赏图片 学生:欣赏图片,初步认识杨辉三角. 教师提问: 1、对杨辉三角你想了解些什么? 2、同学们猜猜“杨辉三角”这个名字是怎么来的? 学生: 1、提出自己想要了解的问题。 2、总结概括已有的知识点,并与杨辉三角联系到一起。 教师:布置任务,明确任务要求。并进行提问, 学生:动笔计算,按要求做好记录,并派小组代表进行展示交流。 教师提问: 1.我们的探索就由此结束了吗 2.我们还能探索些什么 3.一般研究多项式的哪些要素 学生:对提出的问题进行回答,发现还可以探索其中存在的规律.并且根据多项式的相关概念,确定研究方向。 教师提出:分组研讨,明确任务和要求。 小组合作交流,共同归纳猜想。并派小组代表进行展示交流。 【预设】发现以下规律: (1)项数等于次数加1。即:项数为 n+1. (2)每个多项式中,各项的次数都相等,都为n次。 (3)系数规律: ①“三角形”两腰上的数字都是1。 ②从第三行开始,每一个数都是上一行与其相邻的两个数之和。 ③每个多项式的系数之和为2n . ④数字的对称性. 教师提出要求,学生书面作答,并展示交流。 展示世界第一位“雪艺家”的创作以及上海峰会中的一面背景墙设计,使学生感受到杨辉三角的价值,引出课题,激发学生的探究兴趣。 通过观察图片,提炼图片中的文字信息,在归纳已学过的知识的基础上,直观的将新问题与已有的数学知识联系到一起,开拓学生思维。 通过收集整理数据,将数据进行汇总,提高学生的归纳概括能力。 在进行多项式的计算时,要重视和强调有关计算过程。 引导学生发现由系数组成的“三角形”便是杨辉三角了。 以学生为中心,尊重学生的主体意识,在学生的主导作用下,完成本次的活动探究。 在引导过程中,要明确探索方向,以及展开式中存在的规律,采用“从特殊到一般”的数学思想,概括归纳一般规律,从而提升自己的能力。 直接得出结论,从而掌握(a+b)n与杨辉三角的一般规律 当堂检测,并在规定时间内完成。从而检验学生当堂知识的掌握情况。
五、总结提升 1.谈谈你在本节课中有哪些收获 (1) 明确 (a+b)n(n=0,1,2,3,…)的展开式中的项数、项的次数、系数的规律。 (2)了解杨辉三角的历史。 六、课后思考 1.再次观察杨辉三角,你还能发现杨辉三角中有哪些有趣的规律? 2.上网查找关于杨辉三角的规律,并和你的同伴进行交流展示。 学生:自行总结本堂活动课的收获。 教师:予以补充。 学生课后完成 温故而知新,通过学生自己归纳学习内容,一方面提升学生的概括能力,另一方面对所学知识加以巩固,内化于心。 通过布置课后思考作业,启发学生了解更多的有关杨辉三角的内容,不断拓宽学生的知识面。
板 书 设 计 (a+b)n与杨辉三角 规律总结:
课 后 反 思 本节内容是八年级上册数学“阅读与思考”中的一项数学探究活动,旨在通过观察杨辉三角的结构特征,从而与多项式(a+b)n的展开式中的系数、项数、次数紧密结合,在探究中找到一般规律,并根据规律解决有关数学问题。 本节课学生的学习积极性普遍较高,上课举手回答问题的学生有所增加,大部分同学都能认真听讲,畅所欲言的提出自己心中的疑问,并在计算和观察记录中,总结归纳出一般规律,解决心中的疑惑,整体效果较好,但也存在很多不足之处。因此今后我会更加重视数学活动的研究,不断阅读与思考与课本知识息息相关的数学活动,让学生们在学习中不断提高自己各方面的能力。
课题 (a+b)n与杨辉三角 课型 新授课 课时 1课时
年级 八年级 时间 节次 1
背景 分析 1.课程标准:通过教师在平时教学中渗透或通过课外阅读,了解杨辉三角的简史,掌握杨辉三角中隐含的基本规律,以拓宽整式乘法。 2.教材分析:本节是在学习了整式乘法的基础上进行探究的,是对整式乘法的拓展,为学习二项式(a+b)n 的展开式奠定基础,通过本节探究杨辉三角规律的教学,既能构建完整知识框架,又能多方位提高学生的数学素养。 3.学情分析: 本学段的学生具有对与自己的直观经验相冲突的现象和对有挑战性任务感兴趣的特点,也初步具备个体和群体参与“探究性问题”、“开放性问题”活动的能力,结合本节内容的特点,采用探究式学习方式,对于学生在探究过程中出现不全面、易出错等问题,教师给予及时的引导、点拨和激励评价。
学习 目标 1、了解(a+b)n(n=0,1,2,3……) 的展开式中的项数、项的次数、系数的规律。 2、探索并归纳展开式中的项数、项的次数、系数的一般规律。 3、了解 “杨辉三角”的历史。
评价 设计 1、采用课堂观察的方式进行评价。 2、采用随堂提问的方式进行评价。 3、采用达标检测的方式进行评价。
问题情境 师生活动 设计意图
一、创设情境,设置悬念 欣赏图片: PPT中出示两张图片,一张为十大杰出艺术家的创作;第二张为上海峰会中的一张照片,照片中的一面背景墙是由“一些特殊数字”组成的“三角形”设计而成. 学生活动: 欣赏图片,初步认识杨辉三角. 【引出课题】 设计的灵感都来源于数学史上一个伟大的发现——“杨辉三角” 二、自主探究 观察图片以及文字信息,联系学过的知识,大胆猜测一下它与什么数学知识有关? 三、合作交流,探索规律 【活动一】收集整理数据 1、计算(a+b)n(n=0,1,2,3,4,5),将结果记录在记录表中。 2、将上述展开后的6个多项式中的系数,填写在记录表中对应的位置上。 任务要求: 结果多项式按a的降幂顺序排列。小组分工协作(计算、检查、记录、整理)。 【活动二】开展分组研讨,探索其中奥秘 1、我们得到了6个多项式以及对应的系数表,相应的也得到了“杨辉三角”。 2、【分组研讨】 【研讨问题1】观察得到的6个多项式,它们的项数有什么规律 【研讨问题2】每个多项式中,各项的次数有什么规律 【研讨问题3】观察系数表,你能发现哪些规律 【活动三】深入猜想验证,激发求知热情 【追问1】你能利用规律直接写出(a+b)7的展开式及系数吗 【追问2】当n=7,8,9,……时,我们怎么来验证呢 用已有的知识能验证“所有”吗 【总结】虽然可以用同样的方法逐一对更高次的情况进行验证,但是由于n可以取到无限大,所以用我们有限的知识和经验是无法完成的. 学无止境,当你学到的知识越来越多时,解决这个问题就是小菜一碟了.高中阶段我们就能深入探索这些规律了. 四、达标检测 1、将图补充完整。 2、直接写出〖( + )〗^5的展开式。 教师:引导学生欣赏图片 学生:欣赏图片,初步认识杨辉三角. 教师提问: 1、对杨辉三角你想了解些什么? 2、同学们猜猜“杨辉三角”这个名字是怎么来的? 学生: 1、提出自己想要了解的问题。 2、总结概括已有的知识点,并与杨辉三角联系到一起。 教师:布置任务,明确任务要求。并进行提问, 学生:动笔计算,按要求做好记录,并派小组代表进行展示交流。 教师提问: 1.我们的探索就由此结束了吗 2.我们还能探索些什么 3.一般研究多项式的哪些要素 学生:对提出的问题进行回答,发现还可以探索其中存在的规律.并且根据多项式的相关概念,确定研究方向。 教师提出:分组研讨,明确任务和要求。 小组合作交流,共同归纳猜想。并派小组代表进行展示交流。 【预设】发现以下规律: (1)项数等于次数加1。即:项数为 n+1. (2)每个多项式中,各项的次数都相等,都为n次。 (3)系数规律: ①“三角形”两腰上的数字都是1。 ②从第三行开始,每一个数都是上一行与其相邻的两个数之和。 ③每个多项式的系数之和为2n . ④数字的对称性. 教师提出要求,学生书面作答,并展示交流。 展示世界第一位“雪艺家”的创作以及上海峰会中的一面背景墙设计,使学生感受到杨辉三角的价值,引出课题,激发学生的探究兴趣。 通过观察图片,提炼图片中的文字信息,在归纳已学过的知识的基础上,直观的将新问题与已有的数学知识联系到一起,开拓学生思维。 通过收集整理数据,将数据进行汇总,提高学生的归纳概括能力。 在进行多项式的计算时,要重视和强调有关计算过程。 引导学生发现由系数组成的“三角形”便是杨辉三角了。 以学生为中心,尊重学生的主体意识,在学生的主导作用下,完成本次的活动探究。 在引导过程中,要明确探索方向,以及展开式中存在的规律,采用“从特殊到一般”的数学思想,概括归纳一般规律,从而提升自己的能力。 直接得出结论,从而掌握(a+b)n与杨辉三角的一般规律 当堂检测,并在规定时间内完成。从而检验学生当堂知识的掌握情况。
五、总结提升 1.谈谈你在本节课中有哪些收获 (1) 明确 (a+b)n(n=0,1,2,3,…)的展开式中的项数、项的次数、系数的规律。 (2)了解杨辉三角的历史。 六、课后思考 1.再次观察杨辉三角,你还能发现杨辉三角中有哪些有趣的规律? 2.上网查找关于杨辉三角的规律,并和你的同伴进行交流展示。 学生:自行总结本堂活动课的收获。 教师:予以补充。 学生课后完成 温故而知新,通过学生自己归纳学习内容,一方面提升学生的概括能力,另一方面对所学知识加以巩固,内化于心。 通过布置课后思考作业,启发学生了解更多的有关杨辉三角的内容,不断拓宽学生的知识面。
板 书 设 计 (a+b)n与杨辉三角 规律总结:
课 后 反 思 本节内容是八年级上册数学“阅读与思考”中的一项数学探究活动,旨在通过观察杨辉三角的结构特征,从而与多项式(a+b)n的展开式中的系数、项数、次数紧密结合,在探究中找到一般规律,并根据规律解决有关数学问题。 本节课学生的学习积极性普遍较高,上课举手回答问题的学生有所增加,大部分同学都能认真听讲,畅所欲言的提出自己心中的疑问,并在计算和观察记录中,总结归纳出一般规律,解决心中的疑惑,整体效果较好,但也存在很多不足之处。因此今后我会更加重视数学活动的研究,不断阅读与思考与课本知识息息相关的数学活动,让学生们在学习中不断提高自己各方面的能力。
