沪教版(上海)数学八年级第二学期 第二十二章四边形 梯形复习教案(表格式)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期 第二十二章四边形 梯形复习教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 120.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 06:31:51 | ||
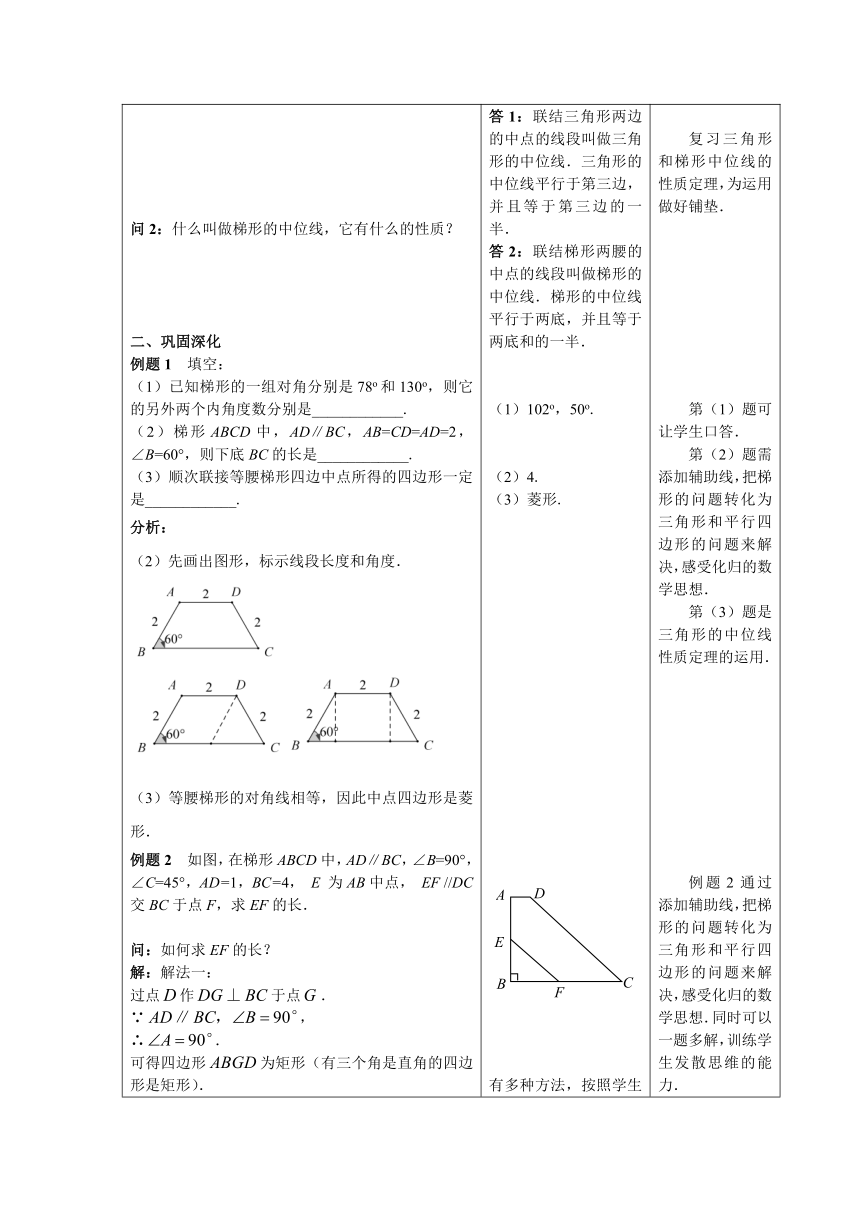
图片预览

文档简介
第二十二章 四边形(梯形)复习
普陀区课题组
教学目标:
1.理解梯形及其有关概念,知道梯形与平行四边形的区别和联系.
2.理解三角形和梯形之间的联系,感受化归的数学思想.
3.通过一题多解的教学,培养发散性思维能力.
4.掌握三角形和梯形中位线的性质定理,能运用定理进行计算和推理论证.
教学重点:梯形相关定理的灵活运用.
教学难点:梯形辅助线的添加.
教学过程:
教师活动 学生活动 教学设计意图
一、知识梳理 1.梯形 问1:梯形的定义? 问2:我们学过哪些特殊的梯形? 问3:等腰梯形的判定方法有哪些? 问4:等腰梯形有哪些性质呢?请完成下表的填写. (
图形的性质
边
角
对角线
对称性
等腰梯形
两底平行,
两腰相等
同一底上的两个角相等
两条对角线相等
轴对称图形
) 师:至此,四边形的分类可以直观地用下图来表示: 2.三角形和梯形中位线 问1:什么叫做三角形的中位线,它有什么的性质? 问2:什么叫做梯形的中位线,它有什么的性质? 二、巩固深化 例题1 填空: (1)已知梯形的一组对角分别是78o和130o,则它的另外两个内角度数分别是____________. (2)梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,则下底BC的长是____________. (3)顺次联接等腰梯形四边中点所得的四边形一定是____________. 分析: (2)先画出图形,标示线段长度和角度. (3)等腰梯形的对角线相等,因此中点四边形是菱形. 例题2 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4, E 为AB中点, EF //DC交BC于点F,求EF的长. 问:如何求EF的长? 解:解法一: 过点作于点. ∵, ∴. 可得四边形为矩形(有三个角是直角的四边形是矩形). ∴BG=AD=1,AB=DG(矩形的对边相等). ∵, ∴. ∵, ∴. ∴. ∴. 又∵为中点, ∴. ∵EF //DC, ∴. 在中,, ∴EF=BE=. 解法二: 取DC的中点G,联结EG, ∵E、G分别是AB、DC的中点, ∴EG=(AD+BC),EG//BC(梯形的中位线平行于两底,并且等于两底和的一半). ∵AD=1,BC=4, ∴EG=. ∵EF //DC, ∴EFCG是平行四边形(两组对边分别平行的四边形是平行四边形). ∴EG=FC=(平行四边形的对边相等). ∴EF=4 =. 在中,, ∴EF=BE=. (
A
D
B
E
C
F
G
) (
A
D
B
E
C
F
G
3
1
2
)还有其他解法,解略. 【适时小结】 1.梯形中常用的辅助线: 2.中点四边形一定是平行四边形,四边形的形状由原四边形的对角线决定: 对角线相等菱形; 对角线垂直矩形. 三、课堂练习 如图:在梯形ABCD中,AD∥BC,CA平分∠BCD,延长BC至点E,使CE=AD,∠B=2∠E. (1)求证:四边形ABCD是等腰梯形; (2)若∠B=60o,AB=4,求边BC的长. (
A
B
C
E
D
) 四、课堂小结 谈谈这节课你有什么收获、体会或想法 教师补充:化归、图形的分解组合的数学思想. 五、布置作业 练习册:复习题 答1:一组对边平行而另一组对边不平行的四边形叫做梯形. 答2:直角梯形和等腰梯形. 答3:(1)两腰相等的梯形是等腰梯形;(2)同一底角上的两个角相等的梯形是等腰梯形;(3)对角线相等的梯形是等腰梯形. 答1:联结三角形两边的中点的线段叫做三角形的中位线.三角形的中位线平行于第三边,并且等于第三边的一半. 答2:联结梯形两腰的中点的线段叫做梯形的中位线.梯形的中位线平行于两底,并且等于两底和的一半. (1)102o,50o. (2)4. (3)菱形. (
A
D
B
E
C
F
) 有多种方法,按照学生的说法来分析. (
A
D
B
E
C
F
G
) (
A
D
B
E
C
F
G
) (1)∵AD∥CE,CE=AD,∴四边形ADEC是平行四边形, ∴AC∥DE, ∴∠ACB=∠E. ∵CA平分∠BCD, ∴∠ACB=∠ACD. 即:∠BCD=2∠ACB. ∵∠B=2∠E, ∴∠B=∠BCD. ∵四边形ABCD是梯形,∴四边形ABCD是等腰梯形. (2)∵∠B=60o, ∴∠BCD=60o, ∴∠ACB=30o. 在△ABC中,∠B+∠ACB+∠BAC=180o, ∴∠BAC=90o, ∴AB=BC. ∵AB=4,∴BC=8. 预设学生: 1.等腰梯形的性质与判定. 2.三角形和梯形中位线的性质定理. 3.梯形常用的辅助线. 通过梳理知识,培养归纳、总结能力,形成知识系统,为运用做好铺垫. 用集合文氏图表示四边形之间的关系. 复习三角形和梯形中位线的性质定理,为运用做好铺垫. 第(1)题可让学生口答. 第(2)题需添加辅助线,把梯形的问题转化为三角形和平行四边形的问题来解决,感受化归的数学思想. 第(3)题是三角形的中位线性质定理的运用. 例题2通过添加辅助线,把梯形的问题转化为三角形和平行四边形的问题来解决,感受化归的数学思想.同时可以一题多解,训练学生发散思维的能力. 解法一是作高. 解法二是作梯形的中位线. 还可以关于一腰的中点建构中心对称的全等三角形;或延长两腰把梯形转化为三角形. 小结梯形添加辅助线的方法和决定中点四边形形状的关键. 巩固判定等腰梯形的方法. 梳理知识点,培养学生归纳反思的能力.
普陀区课题组
教学目标:
1.理解梯形及其有关概念,知道梯形与平行四边形的区别和联系.
2.理解三角形和梯形之间的联系,感受化归的数学思想.
3.通过一题多解的教学,培养发散性思维能力.
4.掌握三角形和梯形中位线的性质定理,能运用定理进行计算和推理论证.
教学重点:梯形相关定理的灵活运用.
教学难点:梯形辅助线的添加.
教学过程:
教师活动 学生活动 教学设计意图
一、知识梳理 1.梯形 问1:梯形的定义? 问2:我们学过哪些特殊的梯形? 问3:等腰梯形的判定方法有哪些? 问4:等腰梯形有哪些性质呢?请完成下表的填写. (
图形的性质
边
角
对角线
对称性
等腰梯形
两底平行,
两腰相等
同一底上的两个角相等
两条对角线相等
轴对称图形
) 师:至此,四边形的分类可以直观地用下图来表示: 2.三角形和梯形中位线 问1:什么叫做三角形的中位线,它有什么的性质? 问2:什么叫做梯形的中位线,它有什么的性质? 二、巩固深化 例题1 填空: (1)已知梯形的一组对角分别是78o和130o,则它的另外两个内角度数分别是____________. (2)梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,则下底BC的长是____________. (3)顺次联接等腰梯形四边中点所得的四边形一定是____________. 分析: (2)先画出图形,标示线段长度和角度. (3)等腰梯形的对角线相等,因此中点四边形是菱形. 例题2 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4, E 为AB中点, EF //DC交BC于点F,求EF的长. 问:如何求EF的长? 解:解法一: 过点作于点. ∵, ∴. 可得四边形为矩形(有三个角是直角的四边形是矩形). ∴BG=AD=1,AB=DG(矩形的对边相等). ∵, ∴. ∵, ∴. ∴. ∴. 又∵为中点, ∴. ∵EF //DC, ∴. 在中,, ∴EF=BE=. 解法二: 取DC的中点G,联结EG, ∵E、G分别是AB、DC的中点, ∴EG=(AD+BC),EG//BC(梯形的中位线平行于两底,并且等于两底和的一半). ∵AD=1,BC=4, ∴EG=. ∵EF //DC, ∴EFCG是平行四边形(两组对边分别平行的四边形是平行四边形). ∴EG=FC=(平行四边形的对边相等). ∴EF=4 =. 在中,, ∴EF=BE=. (
A
D
B
E
C
F
G
) (
A
D
B
E
C
F
G
3
1
2
)还有其他解法,解略. 【适时小结】 1.梯形中常用的辅助线: 2.中点四边形一定是平行四边形,四边形的形状由原四边形的对角线决定: 对角线相等菱形; 对角线垂直矩形. 三、课堂练习 如图:在梯形ABCD中,AD∥BC,CA平分∠BCD,延长BC至点E,使CE=AD,∠B=2∠E. (1)求证:四边形ABCD是等腰梯形; (2)若∠B=60o,AB=4,求边BC的长. (
A
B
C
E
D
) 四、课堂小结 谈谈这节课你有什么收获、体会或想法 教师补充:化归、图形的分解组合的数学思想. 五、布置作业 练习册:复习题 答1:一组对边平行而另一组对边不平行的四边形叫做梯形. 答2:直角梯形和等腰梯形. 答3:(1)两腰相等的梯形是等腰梯形;(2)同一底角上的两个角相等的梯形是等腰梯形;(3)对角线相等的梯形是等腰梯形. 答1:联结三角形两边的中点的线段叫做三角形的中位线.三角形的中位线平行于第三边,并且等于第三边的一半. 答2:联结梯形两腰的中点的线段叫做梯形的中位线.梯形的中位线平行于两底,并且等于两底和的一半. (1)102o,50o. (2)4. (3)菱形. (
A
D
B
E
C
F
) 有多种方法,按照学生的说法来分析. (
A
D
B
E
C
F
G
) (
A
D
B
E
C
F
G
) (1)∵AD∥CE,CE=AD,∴四边形ADEC是平行四边形, ∴AC∥DE, ∴∠ACB=∠E. ∵CA平分∠BCD, ∴∠ACB=∠ACD. 即:∠BCD=2∠ACB. ∵∠B=2∠E, ∴∠B=∠BCD. ∵四边形ABCD是梯形,∴四边形ABCD是等腰梯形. (2)∵∠B=60o, ∴∠BCD=60o, ∴∠ACB=30o. 在△ABC中,∠B+∠ACB+∠BAC=180o, ∴∠BAC=90o, ∴AB=BC. ∵AB=4,∴BC=8. 预设学生: 1.等腰梯形的性质与判定. 2.三角形和梯形中位线的性质定理. 3.梯形常用的辅助线. 通过梳理知识,培养归纳、总结能力,形成知识系统,为运用做好铺垫. 用集合文氏图表示四边形之间的关系. 复习三角形和梯形中位线的性质定理,为运用做好铺垫. 第(1)题可让学生口答. 第(2)题需添加辅助线,把梯形的问题转化为三角形和平行四边形的问题来解决,感受化归的数学思想. 第(3)题是三角形的中位线性质定理的运用. 例题2通过添加辅助线,把梯形的问题转化为三角形和平行四边形的问题来解决,感受化归的数学思想.同时可以一题多解,训练学生发散思维的能力. 解法一是作高. 解法二是作梯形的中位线. 还可以关于一腰的中点建构中心对称的全等三角形;或延长两腰把梯形转化为三角形. 小结梯形添加辅助线的方法和决定中点四边形形状的关键. 巩固判定等腰梯形的方法. 梳理知识点,培养学生归纳反思的能力.
