北师大版六年级数学下册3.欣赏与设计同步练习(含答案)
文档属性
| 名称 | 北师大版六年级数学下册3.欣赏与设计同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 551.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 16:05:10 | ||
图片预览



文档简介
北师大版 六年级数学下册
3.4 欣赏与设计 同步练习 (含答案)
一、填空题
1.将某一图形进行( ),( )或者画出关于某条直线的轴对称图形,可以设计出美丽的图案。
2.长方形有( )条对称轴,正方形有( )条对称轴,圆有( )条对称轴。
3.利用图形的轴对称、( )和( )变换可以设计出美丽的图案。
4.下图是由几种完全一样的图形拼成的图案,请你先在图案中找出基本图形,它们分别是( )、( )、( )和( )。
(第4题) (第5题)
5.下图可以看成由一个三角形旋转而成的,它一共旋转( )次,分别旋转( )而形成的。
二、选择题
6.下面的图案中利用旋转设计的是( )。
A. B. C. D.
7.下列图形中,对称轴条数最多的是( )。
A.长方形 B.正方形 C.等边三角形 D.圆形
8.下面图形中,由旋转得来的图形是( )。
A. B. C. D.
9.下面的图形能用旋转作出的共有( )。
A.1个 B.2个 C.3个 D.4个
10.下面的4个图案中,既包含图形的旋转,还是轴对称图形的是( )。
A. B. C. D.
11.下面图形绕O点顺时针旋转90°后的图形是( ),顺时针旋转180°的图形是( )。 ( )
① ② ③
A.②① B.③① C.③② D.②③
12.下列图案中,可有由“基本图形”连续旋转45°得到的是( ).
A. B. C. D.
13.下面的图形经过一定的角度旋转,都可以与原来的图形重合,与原来的图形重合时旋转角度最小的是( )。
A. B. C. D.
14.下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形 B.长方形 C.圆 D.平行四边形
三、判断题
15.利用平移,旋转可以设计许多美丽的图案。( )
16.通过平移就可以的得到所有图形。( )
17.一个半圆通过旋转能得到这样一个图案。( )
18.当禁止通行时,公路收费站的横杆一定是按逆时针方向旋转了90度. ( )
19.把一个图按1:3的比缩小后,周长会比原来缩小3倍,面积会比原来缩小6倍.( )
20.一棵小树被扶种好,这棵小树一定绕树脚逆时针方向旋转了90度。( )
四、解答题
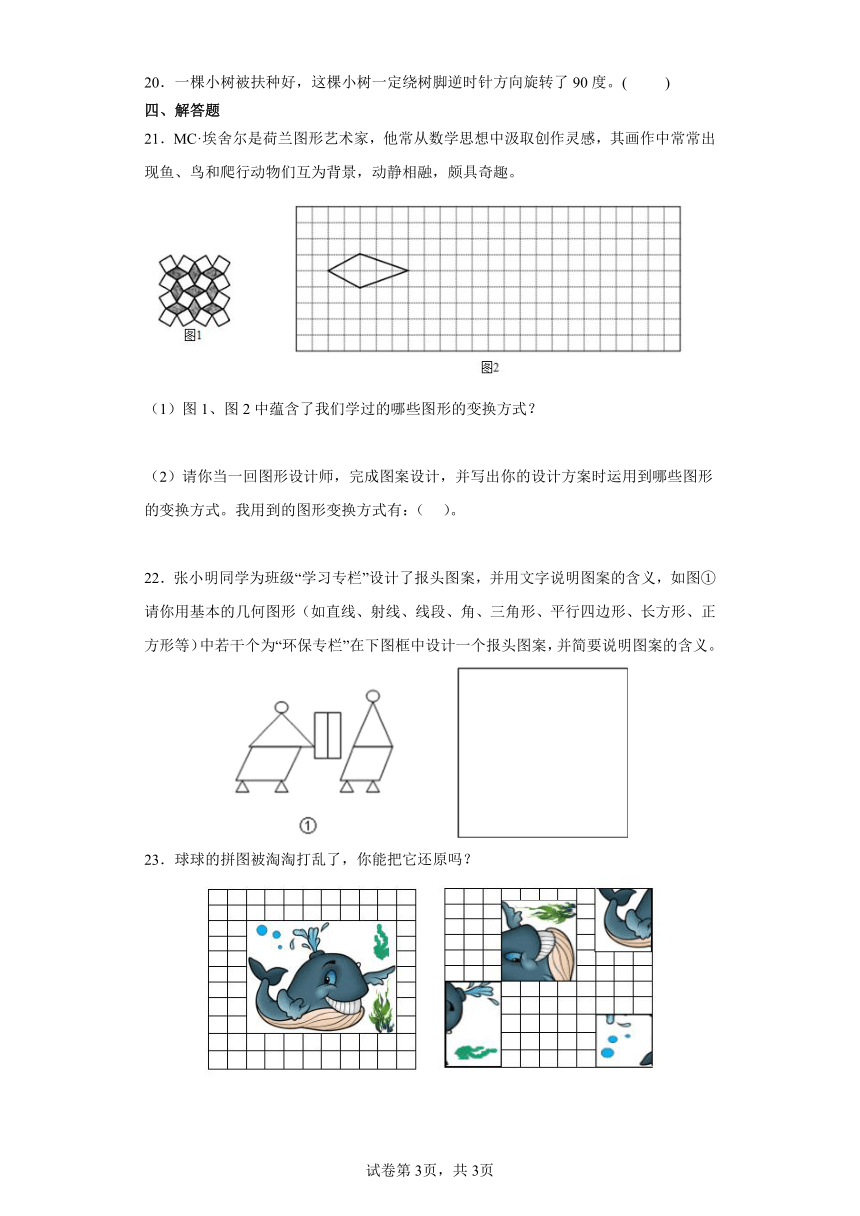
21.MC·埃舍尔是荷兰图形艺术家,他常从数学思想中汲取创作灵感,其画作中常常出现鱼、鸟和爬行动物们互为背景,动静相融,颇具奇趣。
(1)图1、图2中蕴含了我们学过的哪些图形的变换方式?
(2)请你当一回图形设计师,完成图案设计,并写出你的设计方案时运用到哪些图形的变换方式。我用到的图形变换方式有:( )。
22.张小明同学为班级“学习专栏”设计了报头图案,并用文字说明图案的含义,如图①请你用基本的几何图形(如直线、射线、线段、角、三角形、平行四边形、长方形、正方形等)中若干个为“环保专栏”在下图框中设计一个报头图案,并简要说明图案的含义。
23.球球的拼图被淘淘打乱了,你能把它还原吗?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1. 平移 旋转
【分析】将某一图形进行平移,旋转或者画出关于某条直线的轴对称图形,可以设计出一个美丽的图案,据此解答即可。
【详解】将某一图形进行平移,旋转或者画出关于某条直线的轴对称图形。
2. 2 4 无数
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,根据对称轴定义找出各图形对称轴的数量。
【详解】长方形的对称轴:每组对边中点连线所在的直线,共有2条对称轴;
正方形的对称轴:每组对边中点连线所在的直线,对角线所在的直线,共有4条对称轴;
圆形的对称轴:将一张圆形纸片对折,折线两侧的部分可以完全重合,圆有无数条对称轴。
由上可知,长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
3. 平移 旋转
【详解】利用对称、平移和旋转的变换可以设计出美丽的图案。
例如蜜蜂的蜂窝就是利用正六边形的对称、平移和旋转的变换得到的图案。
4. 六边形 五边形 正方形 三角形
【分析】仔细观察图,将看到的基本图形圈起来,最后数一数,有哪几种图形即可得到解答。
【详解】根据题意将图整理如下:
基本图形有六边形、五边形、正方形、填空题。
5. 7 45°、90°、135°、180°、225°、270°、315°
6.B
【分析】根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,进行解答即可。
【详解】A.经过轴对称得到的;
B.图中一个图形绕某点和按顺时针(或逆时针)方向旋转得到的;
C.经过轴对称得到的;
D.经过平移得到的。
故答案为:B
7.D
【分析】长方形有两条对称轴,也就是过对边中点的直线;正方形有四条对称轴,即过对边中点的直线和过对角的直线;等边三角形有三条对称轴,即三条高所在的直线;圆形有无数条对称轴,即直径所在的直线。
【详解】A.长方形有两条对称轴;
B. 正方形有四条对称轴;
C. 等边三角形有三条对称轴;
D. 圆形有无数条对称轴;
故答案为:D
8.C
【分析】根据旋转的定义,把一个图形绕着某一点转动一定的角度的图形变换叫做旋转;据此进行解答。
【详解】旋转的特点是:只改变图形的位置,不改变图形的形状和大小,A、B、D项改变了图形的形状,所以C项正确。
故答案为:C。
9.D
10.D
11.A
【详解】图形绕O点顺时针旋转90°后的图形开口向下,故为③,顺时针旋转180°开口向左,故为①.
所以选择A。
12.B
【详解】图形旋转一周是360度,360÷45=8(个),即有8个均匀分布的基本图形才符合要求,故填B.
13.C
14.B
【详解】在推导三角形、平行四边形、圆的面积公式时,用到平移或旋转,而长方形的面积是利用数格子的方法推导的。
故答案为:B
15.√
【分析】将一个图形按照一定的方向、距离平移,按照一定的方向和角度进行旋转即可得到许多美丽的图案。
【详解】根据分析可知,利用平移,旋转可以设计许多美丽的图案。
原题说法正确。
故答案为:√
16.×
【分析】有的图形可以通过轴对称得到、有的图形可以通过旋转得到,有的可以通过平移得到、有的图形综合用到平移、旋转、轴对称等方式得到。据此解答。
【详解】据分析知:通过平移不能得到所有图形。故原题说法错误。
17.√
【分析】在平面内,将一个图形绕一点按某一个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】一个半圆通过旋转能得到这样一个图案。说法正确。
故答案为:√
18.×
【详解】当禁止通行时,公路收费站的横杆可能绕树脚逆时针方向旋转了90度,也可能绕树脚顺时针方向旋转了90度.
19.错误
【详解】把一个图按1:3的比缩小后,周长会比原来缩小2倍,面积会比原来缩小8倍.
20.×
【详解】一棵小树被扶种好,这棵小树可能绕树脚逆时针方向旋转了90度,也可能绕树脚顺时针方向旋转了90度。
21.(1)平移;旋转;轴对称;
(2)图见详解;旋转
【分析】(1)根据平移和旋转的特征,观察图一运用了哪种变换方式即可。
(2)根据平移和旋转的特征设计方案,答案不唯一。
【详解】(1)通过观察可知相同颜色的图形,通过平移可以得到,不同颜色的图形,通过旋转可以得到。所以图1蕴含了我们学过的平移和旋转的变换方式。图2可以通过轴对称得到,图2的上半部分和下半部分通过中间的直线可以重合,所以是轴对称图形,可以通过轴对称得到。所以图2蕴含了我们学过的轴对称变换方式。
(2)如图:
我用到的图形的变换方式有旋转。
22.【分析】本题是开放型发散思维的题目,答案不唯一,合理即可。
【详解】
含义:请走近垃圾箱,将垃圾放入箱内。
23.【详解】答:(1)图形1逆时针旋转90°向上平移,再向右平移;
(2)图形2顺时针旋转90°;
(3)图形3顺时针旋转90°再向左平移,然后向上平移;
(4)图形4 先向下平移再向左平移即可得到原图形。
答案第1页,共2页
答案第1页,共2页
3.4 欣赏与设计 同步练习 (含答案)
一、填空题
1.将某一图形进行( ),( )或者画出关于某条直线的轴对称图形,可以设计出美丽的图案。
2.长方形有( )条对称轴,正方形有( )条对称轴,圆有( )条对称轴。
3.利用图形的轴对称、( )和( )变换可以设计出美丽的图案。
4.下图是由几种完全一样的图形拼成的图案,请你先在图案中找出基本图形,它们分别是( )、( )、( )和( )。
(第4题) (第5题)
5.下图可以看成由一个三角形旋转而成的,它一共旋转( )次,分别旋转( )而形成的。
二、选择题
6.下面的图案中利用旋转设计的是( )。
A. B. C. D.
7.下列图形中,对称轴条数最多的是( )。
A.长方形 B.正方形 C.等边三角形 D.圆形
8.下面图形中,由旋转得来的图形是( )。
A. B. C. D.
9.下面的图形能用旋转作出的共有( )。
A.1个 B.2个 C.3个 D.4个
10.下面的4个图案中,既包含图形的旋转,还是轴对称图形的是( )。
A. B. C. D.
11.下面图形绕O点顺时针旋转90°后的图形是( ),顺时针旋转180°的图形是( )。 ( )
① ② ③
A.②① B.③① C.③② D.②③
12.下列图案中,可有由“基本图形”连续旋转45°得到的是( ).
A. B. C. D.
13.下面的图形经过一定的角度旋转,都可以与原来的图形重合,与原来的图形重合时旋转角度最小的是( )。
A. B. C. D.
14.下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形 B.长方形 C.圆 D.平行四边形
三、判断题
15.利用平移,旋转可以设计许多美丽的图案。( )
16.通过平移就可以的得到所有图形。( )
17.一个半圆通过旋转能得到这样一个图案。( )
18.当禁止通行时,公路收费站的横杆一定是按逆时针方向旋转了90度. ( )
19.把一个图按1:3的比缩小后,周长会比原来缩小3倍,面积会比原来缩小6倍.( )
20.一棵小树被扶种好,这棵小树一定绕树脚逆时针方向旋转了90度。( )
四、解答题
21.MC·埃舍尔是荷兰图形艺术家,他常从数学思想中汲取创作灵感,其画作中常常出现鱼、鸟和爬行动物们互为背景,动静相融,颇具奇趣。
(1)图1、图2中蕴含了我们学过的哪些图形的变换方式?
(2)请你当一回图形设计师,完成图案设计,并写出你的设计方案时运用到哪些图形的变换方式。我用到的图形变换方式有:( )。
22.张小明同学为班级“学习专栏”设计了报头图案,并用文字说明图案的含义,如图①请你用基本的几何图形(如直线、射线、线段、角、三角形、平行四边形、长方形、正方形等)中若干个为“环保专栏”在下图框中设计一个报头图案,并简要说明图案的含义。
23.球球的拼图被淘淘打乱了,你能把它还原吗?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1. 平移 旋转
【分析】将某一图形进行平移,旋转或者画出关于某条直线的轴对称图形,可以设计出一个美丽的图案,据此解答即可。
【详解】将某一图形进行平移,旋转或者画出关于某条直线的轴对称图形。
2. 2 4 无数
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,根据对称轴定义找出各图形对称轴的数量。
【详解】长方形的对称轴:每组对边中点连线所在的直线,共有2条对称轴;
正方形的对称轴:每组对边中点连线所在的直线,对角线所在的直线,共有4条对称轴;
圆形的对称轴:将一张圆形纸片对折,折线两侧的部分可以完全重合,圆有无数条对称轴。
由上可知,长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
3. 平移 旋转
【详解】利用对称、平移和旋转的变换可以设计出美丽的图案。
例如蜜蜂的蜂窝就是利用正六边形的对称、平移和旋转的变换得到的图案。
4. 六边形 五边形 正方形 三角形
【分析】仔细观察图,将看到的基本图形圈起来,最后数一数,有哪几种图形即可得到解答。
【详解】根据题意将图整理如下:
基本图形有六边形、五边形、正方形、填空题。
5. 7 45°、90°、135°、180°、225°、270°、315°
6.B
【分析】根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,进行解答即可。
【详解】A.经过轴对称得到的;
B.图中一个图形绕某点和按顺时针(或逆时针)方向旋转得到的;
C.经过轴对称得到的;
D.经过平移得到的。
故答案为:B
7.D
【分析】长方形有两条对称轴,也就是过对边中点的直线;正方形有四条对称轴,即过对边中点的直线和过对角的直线;等边三角形有三条对称轴,即三条高所在的直线;圆形有无数条对称轴,即直径所在的直线。
【详解】A.长方形有两条对称轴;
B. 正方形有四条对称轴;
C. 等边三角形有三条对称轴;
D. 圆形有无数条对称轴;
故答案为:D
8.C
【分析】根据旋转的定义,把一个图形绕着某一点转动一定的角度的图形变换叫做旋转;据此进行解答。
【详解】旋转的特点是:只改变图形的位置,不改变图形的形状和大小,A、B、D项改变了图形的形状,所以C项正确。
故答案为:C。
9.D
10.D
11.A
【详解】图形绕O点顺时针旋转90°后的图形开口向下,故为③,顺时针旋转180°开口向左,故为①.
所以选择A。
12.B
【详解】图形旋转一周是360度,360÷45=8(个),即有8个均匀分布的基本图形才符合要求,故填B.
13.C
14.B
【详解】在推导三角形、平行四边形、圆的面积公式时,用到平移或旋转,而长方形的面积是利用数格子的方法推导的。
故答案为:B
15.√
【分析】将一个图形按照一定的方向、距离平移,按照一定的方向和角度进行旋转即可得到许多美丽的图案。
【详解】根据分析可知,利用平移,旋转可以设计许多美丽的图案。
原题说法正确。
故答案为:√
16.×
【分析】有的图形可以通过轴对称得到、有的图形可以通过旋转得到,有的可以通过平移得到、有的图形综合用到平移、旋转、轴对称等方式得到。据此解答。
【详解】据分析知:通过平移不能得到所有图形。故原题说法错误。
17.√
【分析】在平面内,将一个图形绕一点按某一个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】一个半圆通过旋转能得到这样一个图案。说法正确。
故答案为:√
18.×
【详解】当禁止通行时,公路收费站的横杆可能绕树脚逆时针方向旋转了90度,也可能绕树脚顺时针方向旋转了90度.
19.错误
【详解】把一个图按1:3的比缩小后,周长会比原来缩小2倍,面积会比原来缩小8倍.
20.×
【详解】一棵小树被扶种好,这棵小树可能绕树脚逆时针方向旋转了90度,也可能绕树脚顺时针方向旋转了90度。
21.(1)平移;旋转;轴对称;
(2)图见详解;旋转
【分析】(1)根据平移和旋转的特征,观察图一运用了哪种变换方式即可。
(2)根据平移和旋转的特征设计方案,答案不唯一。
【详解】(1)通过观察可知相同颜色的图形,通过平移可以得到,不同颜色的图形,通过旋转可以得到。所以图1蕴含了我们学过的平移和旋转的变换方式。图2可以通过轴对称得到,图2的上半部分和下半部分通过中间的直线可以重合,所以是轴对称图形,可以通过轴对称得到。所以图2蕴含了我们学过的轴对称变换方式。
(2)如图:
我用到的图形的变换方式有旋转。
22.【分析】本题是开放型发散思维的题目,答案不唯一,合理即可。
【详解】
含义:请走近垃圾箱,将垃圾放入箱内。
23.【详解】答:(1)图形1逆时针旋转90°向上平移,再向右平移;
(2)图形2顺时针旋转90°;
(3)图形3顺时针旋转90°再向左平移,然后向上平移;
(4)图形4 先向下平移再向左平移即可得到原图形。
答案第1页,共2页
答案第1页,共2页
