8.6.3 平面与平面垂直(第1课时) 课件(共27张PPT)
文档属性
| 名称 | 8.6.3 平面与平面垂直(第1课时) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 17:28:26 | ||
图片预览






文档简介
(共27张PPT)
第八章 立体几何初步
8.6.3 平面与平面垂直
第1课时 面面垂直的判定定理
学习目标
1、理解二面角及其平面角的概念;
2、掌握两个平面垂直的定义及判定定理;
3、能够利用定义及定理解决相关问题;
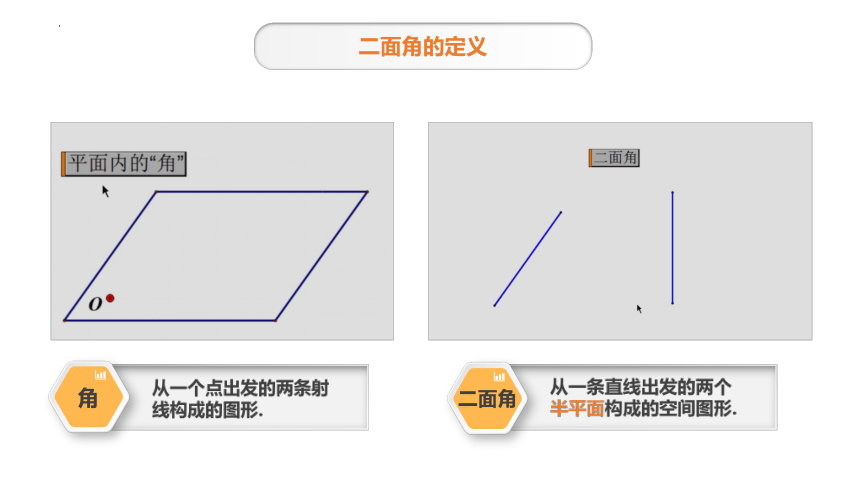
二面角的定义
二面角
角
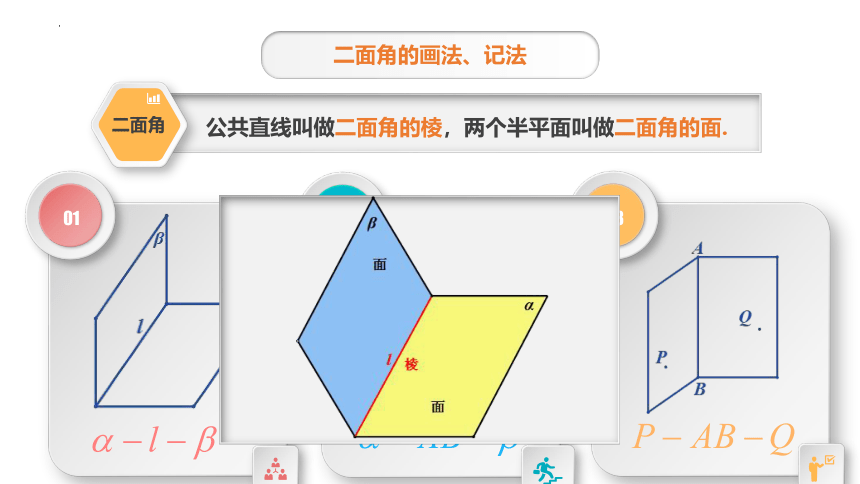
二面角的画法、记法
二面角
公共直线叫做二面角的棱,两个半平面叫做二面角的面.
01
02
03
请举出生活中二面角的例子?
一、二面角及其平面角
2、二面角的概念
如何去衡量二面角大小?
活动:尝试“打开课本”为30°、90°、120°,观察是指哪个角的变化?
问题:回顾如何度量异面直线所成角、直线与平面所成角的大小?
用平面角度量空间角的大小
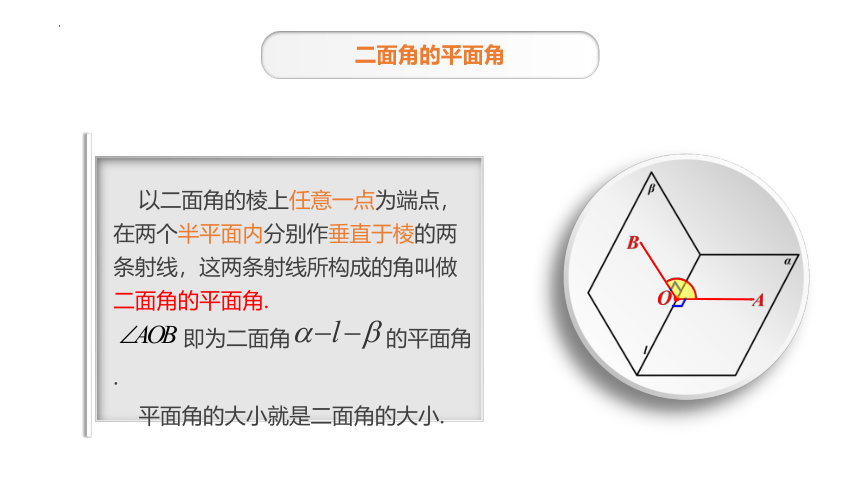
探究活动——二面角的平面角
用空白纸折出一个二面角,讨论后画出一个平面角来表示二面角的大小.
二面角的平面角
以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.
即为二面角 的平面角.
平面角的大小就是二面角的大小.
二面角的平面角
①顶点在棱上;
②两边分别在两个面内;
③边都要垂直于二面角的棱.
二面角的平面角必须满足
二面角的平面角大小与顶点在棱上的位置无关,只与二面角的张角大小有关.
平面角大小的唯一性
二面角的范围
当两个半平面重合时,规定
当两个半平面合成平面时,规定
1、如图,在正方体ABCD -A1B1C1D1中,二面角D1-AB-C的大小是( )
A.30° B.45° C.60° D.90°
B
练习
练习
2、如图,已知四边形ABCD是矩形,PA⊥平面ABCD,且PA=AB,则二面角B-PA-D的平面角的度数为_________
90°
求二面角大小的步骤
简称“一作二证三求”
科普:将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”;
面面垂直的定义
平面角是直角的二面角叫做直二面角;
此时,称两平面互相垂直,记为 .
定义是判定面面
垂直的方法之一.
抢答题
探究活动——判定定理
找到一个面面垂直的实例,指出实例中哪两个平面互相垂直,说明使得该组平面垂直的原因,并尝试总结判定两平面垂直的一般方法
拆
平面与平面垂直的判定定理
证明:
练一练
分析:
面面垂直
线面垂直
线线垂直
练习
例7:如右图,正方体ABCD-A'B'C'D',求证:平面A'BD⊥平面ACC'A'
例7:如右图,正方体ABCD-A'B'C'D',求证:平面A'BD⊥平面ACC'A'
证明:
练习
例8:如图, AB是⊙O的直径, PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点, 求证:平面PAC⊥平面PBC.
练习
∴ BC⊥平面PAC
证明:∵PA⊥面ABC,
BC 面ABC,
∵ C是圆周上不同于A,B的任意一点,AB为⊙O的直径,
又PA∩AC=A,PA、AC 平面PAC,
∴ PA⊥BC,
∴∠BCA=90°, 即BC⊥CA.
∴ 平面PAC⊥平面PBC.
又BC 平面PBC,
二、面面垂直的判定
2、面面垂直的判定
证明面面垂直的步骤
课堂小结
类比
度量
特 殊
平面角
二面角
二面角的
平面角
面面垂直的判定定理
直二面角
文字
语言
图形
语言
符号
语言
用 定义面面垂直
数学思想:
转化的思想方法
面面垂直
线面垂直
线线垂直
练习
3、如图,AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直?为什么?
A
B
C
D
科普:课本P158-例8以及练习的第3题出现的四面体在中国古代被称为“鳖臑”(bie nao),即四个面都是直角三角形的三棱锥.“鳖臑”是用来展示空间垂直关系的经典素材.
知识拓展
底面是直角三角形的直三棱柱称之为“堑堵”.
堑堵
阳马
鳖臑
两个堑堵组成一个长方体
一个阳马和一个鳖臑组成一个堑堵
两个鳖臑组成一个阳马
四个面都是直角三角形的四面体称之为“鳖臑”;
将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”;
练习
4、如图,在正三棱柱ABC-A'B'C'中,D为棱AC的中点,求证:平面BDC'⊥平面ACC'A'
课本P159-练习
练习
【典例】 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=√2a,求证:
(1)PD⊥平面ABCD;
(2)平面PAC⊥平面PBD;
(3)二面角P-BC-D的平面角的大小为45°.
课后作业
1、作业本:《课本》P163-7
2、《课时训练》P63-65
第八章 立体几何初步
8.6.3 平面与平面垂直
第1课时 面面垂直的判定定理
学习目标
1、理解二面角及其平面角的概念;
2、掌握两个平面垂直的定义及判定定理;
3、能够利用定义及定理解决相关问题;
二面角的定义
二面角
角
二面角的画法、记法
二面角
公共直线叫做二面角的棱,两个半平面叫做二面角的面.
01
02
03
请举出生活中二面角的例子?
一、二面角及其平面角
2、二面角的概念
如何去衡量二面角大小?
活动:尝试“打开课本”为30°、90°、120°,观察是指哪个角的变化?
问题:回顾如何度量异面直线所成角、直线与平面所成角的大小?
用平面角度量空间角的大小
探究活动——二面角的平面角
用空白纸折出一个二面角,讨论后画出一个平面角来表示二面角的大小.
二面角的平面角
以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.
即为二面角 的平面角.
平面角的大小就是二面角的大小.
二面角的平面角
①顶点在棱上;
②两边分别在两个面内;
③边都要垂直于二面角的棱.
二面角的平面角必须满足
二面角的平面角大小与顶点在棱上的位置无关,只与二面角的张角大小有关.
平面角大小的唯一性
二面角的范围
当两个半平面重合时,规定
当两个半平面合成平面时,规定
1、如图,在正方体ABCD -A1B1C1D1中,二面角D1-AB-C的大小是( )
A.30° B.45° C.60° D.90°
B
练习
练习
2、如图,已知四边形ABCD是矩形,PA⊥平面ABCD,且PA=AB,则二面角B-PA-D的平面角的度数为_________
90°
求二面角大小的步骤
简称“一作二证三求”
科普:将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”;
面面垂直的定义
平面角是直角的二面角叫做直二面角;
此时,称两平面互相垂直,记为 .
定义是判定面面
垂直的方法之一.
抢答题
探究活动——判定定理
找到一个面面垂直的实例,指出实例中哪两个平面互相垂直,说明使得该组平面垂直的原因,并尝试总结判定两平面垂直的一般方法
拆
平面与平面垂直的判定定理
证明:
练一练
分析:
面面垂直
线面垂直
线线垂直
练习
例7:如右图,正方体ABCD-A'B'C'D',求证:平面A'BD⊥平面ACC'A'
例7:如右图,正方体ABCD-A'B'C'D',求证:平面A'BD⊥平面ACC'A'
证明:
练习
例8:如图, AB是⊙O的直径, PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点, 求证:平面PAC⊥平面PBC.
练习
∴ BC⊥平面PAC
证明:∵PA⊥面ABC,
BC 面ABC,
∵ C是圆周上不同于A,B的任意一点,AB为⊙O的直径,
又PA∩AC=A,PA、AC 平面PAC,
∴ PA⊥BC,
∴∠BCA=90°, 即BC⊥CA.
∴ 平面PAC⊥平面PBC.
又BC 平面PBC,
二、面面垂直的判定
2、面面垂直的判定
证明面面垂直的步骤
课堂小结
类比
度量
特 殊
平面角
二面角
二面角的
平面角
面面垂直的判定定理
直二面角
文字
语言
图形
语言
符号
语言
用 定义面面垂直
数学思想:
转化的思想方法
面面垂直
线面垂直
线线垂直
练习
3、如图,AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直?为什么?
A
B
C
D
科普:课本P158-例8以及练习的第3题出现的四面体在中国古代被称为“鳖臑”(bie nao),即四个面都是直角三角形的三棱锥.“鳖臑”是用来展示空间垂直关系的经典素材.
知识拓展
底面是直角三角形的直三棱柱称之为“堑堵”.
堑堵
阳马
鳖臑
两个堑堵组成一个长方体
一个阳马和一个鳖臑组成一个堑堵
两个鳖臑组成一个阳马
四个面都是直角三角形的四面体称之为“鳖臑”;
将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”;
练习
4、如图,在正三棱柱ABC-A'B'C'中,D为棱AC的中点,求证:平面BDC'⊥平面ACC'A'
课本P159-练习
练习
【典例】 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=√2a,求证:
(1)PD⊥平面ABCD;
(2)平面PAC⊥平面PBD;
(3)二面角P-BC-D的平面角的大小为45°.
课后作业
1、作业本:《课本》P163-7
2、《课时训练》P63-65
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
